Correspondence Analysis and Multiple Correspondence Analysis, and Mediation Analysis
The two topics covered in this module are not related, but they are each useful in their own right.
Mediation Analysis
A common type of analysis that lavaan permits is looking at the role of mediating variables. There are many tools available for specifically looking at 3-variable problems, but lavaan lets you model arbitrarily complex mediation schemes. The analysis of these is more ad hoc though.
The notion of doing a mediation analysis is central to many areas of psychology, especially in social domains where you cannot have complete experimental control. In these cases, you will always have potentially confounding variables, and mediation analysis examines a particular kind of causal relationship. Some of the papers describing mediation are among the top 20 scientific research papers cited in any domain.
The notion is that you may observe a correlation between two variables, but also observe that these may be correlated with a third. For example, you might find that as a population ages from teenager to adult, vehicular accidents go down. But, it might not be age per se that causes this. Instead, it might be practice…as you get older, you get more experience driving, and the experience reduces accidents. Experience may be a mediating variable here. Can all the improvement in driver safety be attributed to experience? Maybe, but to find out, you need to study people who started driving at different ages. This would be a classic mediation test.
Mediation Analysis using psych::mediation
Below is an example data set we can examine mediation. Here, using standard terminology, y is the outcome (accident rate), X is the predictor (age), and M is the mediator variable (experience).
set.seed(1234)
X <- rnorm(100)
M <- 0.5 * X + rnorm(100)
Y <- 0.7 * M + rnorm(100)
M2 <- 0.6 * X + rnorm(100)
Y2 <- 0.6 * X + rnorm(100)
Data <- data.frame(X = X, Y = Y, M = M)
Data2 <- data.frame(X = X, Y = Y2, M = M2)
pairs(Data)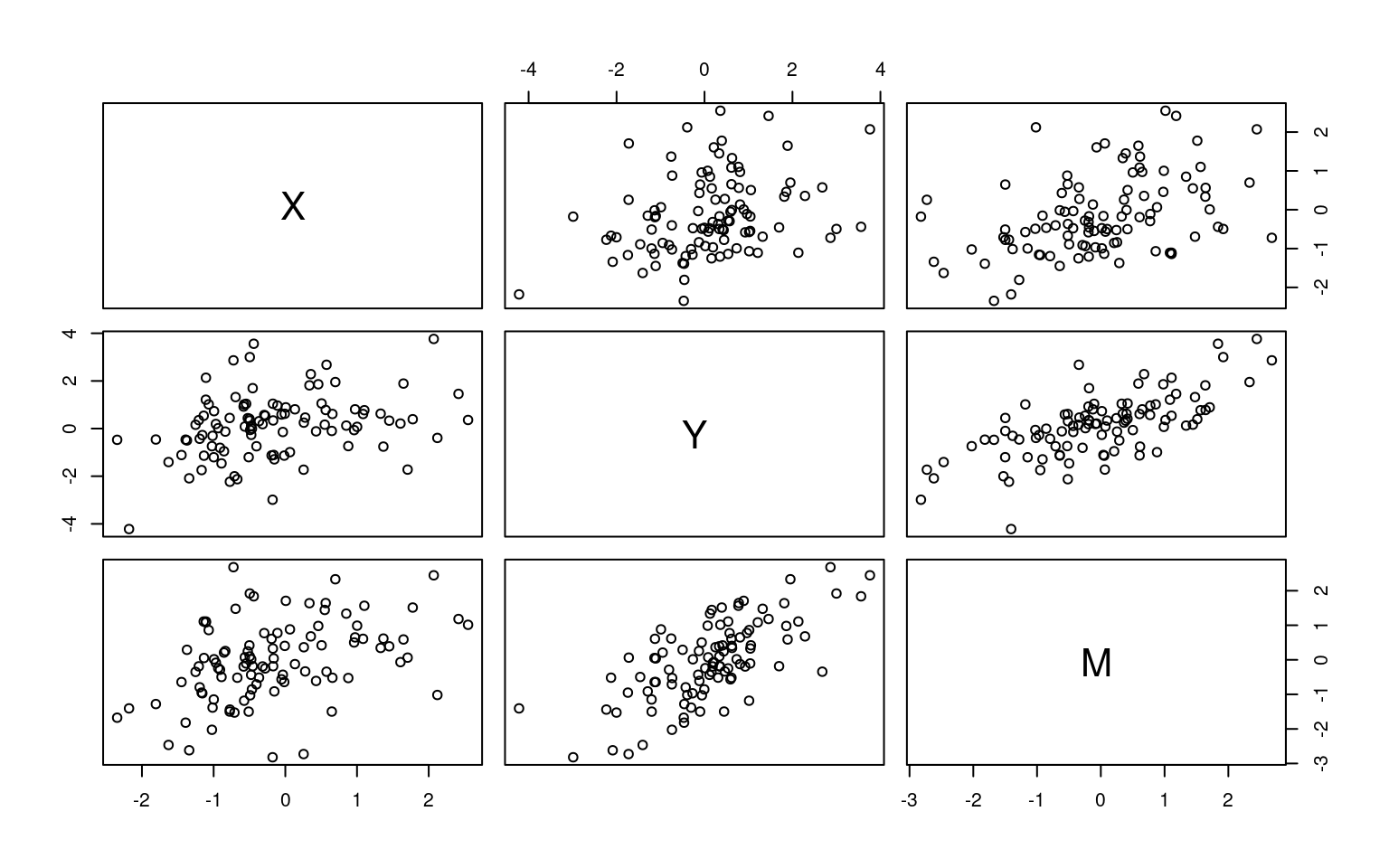
cor(Data) X Y M
X 1.0000000 0.3122748 0.4188856
Y 0.3122748 1.0000000 0.6909791
M 0.4188856 0.6909791 1.0000000pairs(Data2)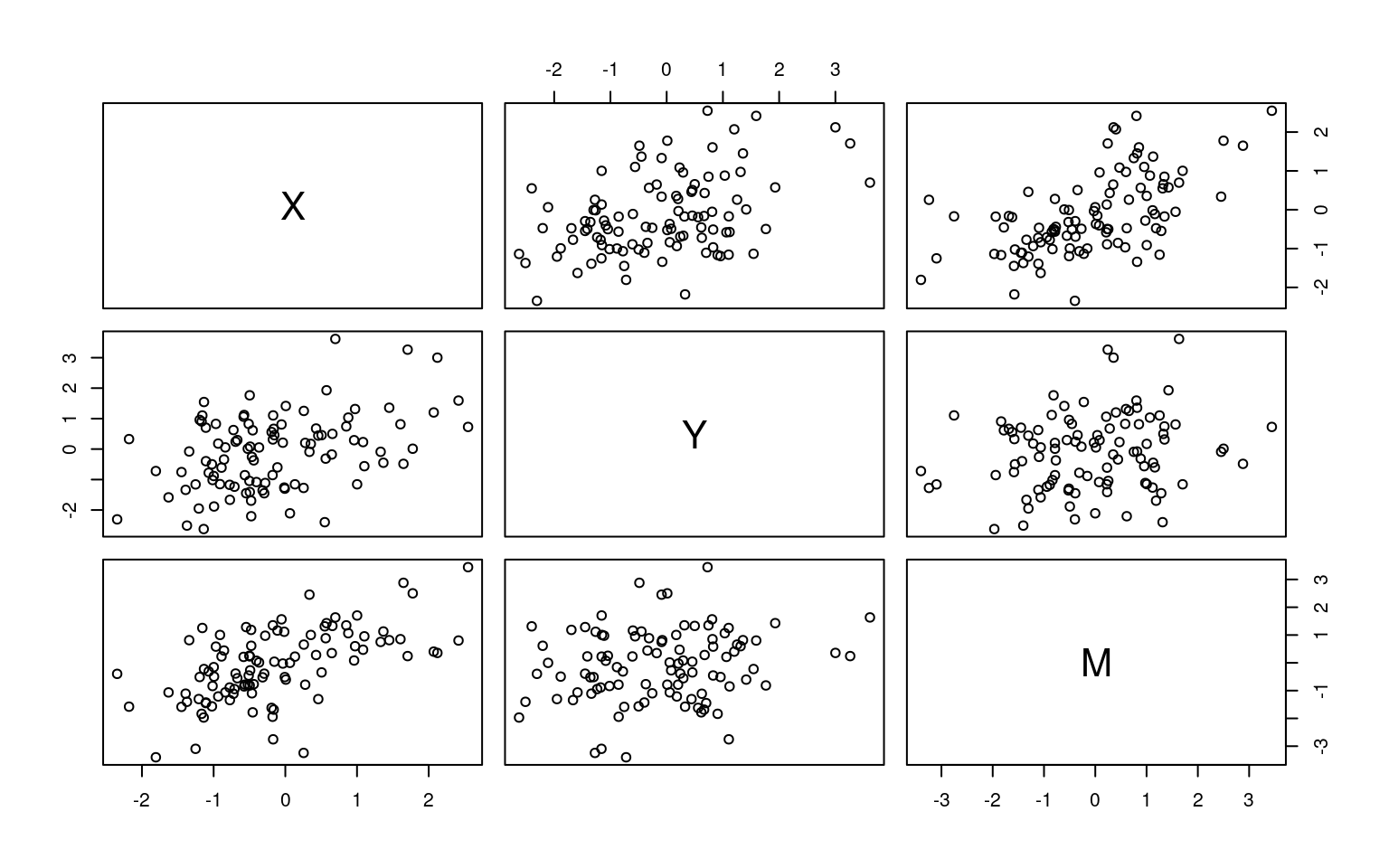
cor(Data2) X Y M
X 1.0000000 0.4255321 0.5857204
Y 0.4255321 1.0000000 0.1827901
M 0.5857204 0.1827901 1.0000000The psych library handles standard mediation analysis using the mediate() function:
library(psych)
m1 <- mediate(Y ~ X + (M), data = Data)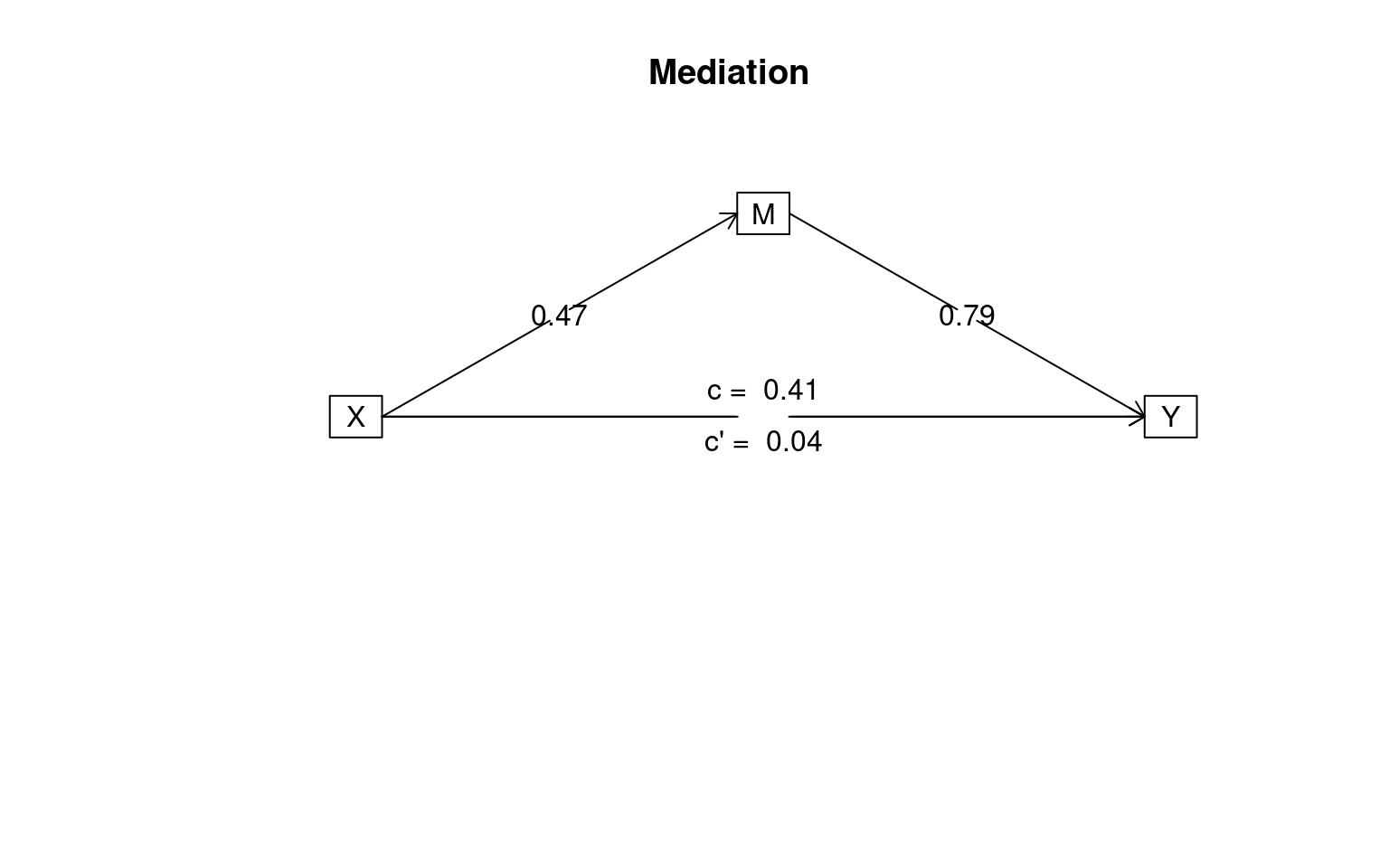
Here, the first model shows the mediated route is has substantial variance along the two legs, and the direct route c diminishes from .41 to .04 when the indirect route is allowed to have an effect, suggesting a strong mediation.
m2 <- mediate(Y ~ X + (M), data = Data2)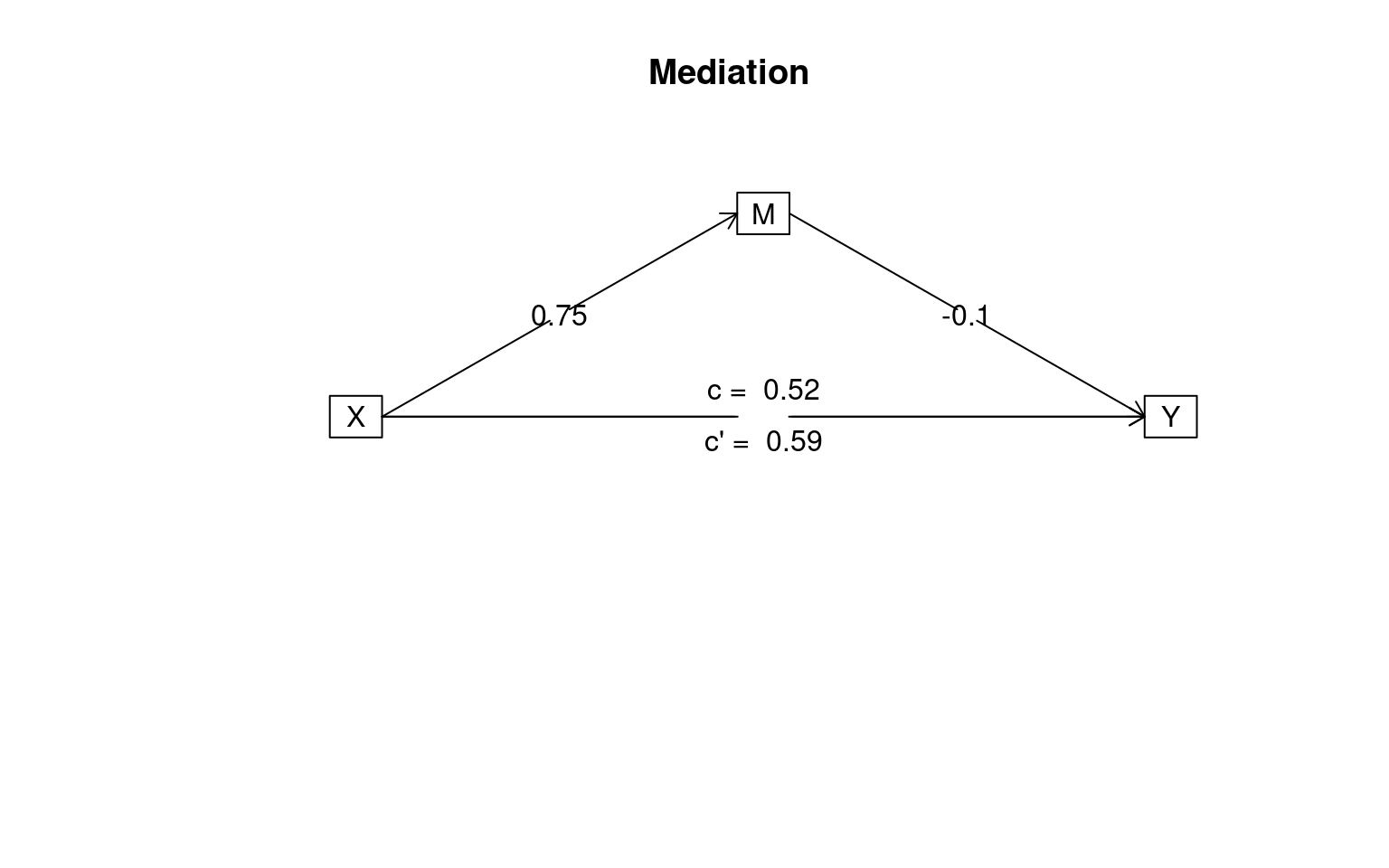
In the second model, there is no correlation along the second leg of the
mediated route, and c and c’ are esesntially the same, indicating M does
not mediate the relationship of x to y.
Mediation using lavaan
So, for both Data and Data2, we have three variables that are all correlated. In truth, for Data, Y is related only to M, but M is related to X. For Data2 both M and Y are related to X directly.
We use ~ to model direct relationships between observed variables.
Here, we will fit a model with a direct relationship between X and Y,
and also another link through M. We need to specify a variable to
represent the interaction of a and b, using
:=, and a final variance total that captures
everthing.
library(lavaan)
library(semPlot)
model <- " # direct effect
Y ~ c*X
# mediator
M ~ a*X
Y ~ b*M
# indirect effect (a*b)
ab := a*b
# total effect
total := c + (a*b)
"
fitmed <- sem(model, data = Data)
summary(fitmed)lavaan 0.6.13 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Y ~
X (c) 0.036 0.104 0.348 0.728
M ~
X (a) 0.474 0.103 4.613 0.000
Y ~
M (b) 0.788 0.092 8.539 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.Y 0.898 0.127 7.071 0.000
.M 1.054 0.149 7.071 0.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
ab 0.374 0.092 4.059 0.000
total 0.410 0.125 3.287 0.001semPaths(fitmed, curvePilot = T, "par", weighted = FALSE, nCharNodes = 7, shapeMan = "rectangle",
sizeMan = 15, sizeMan2 = 10)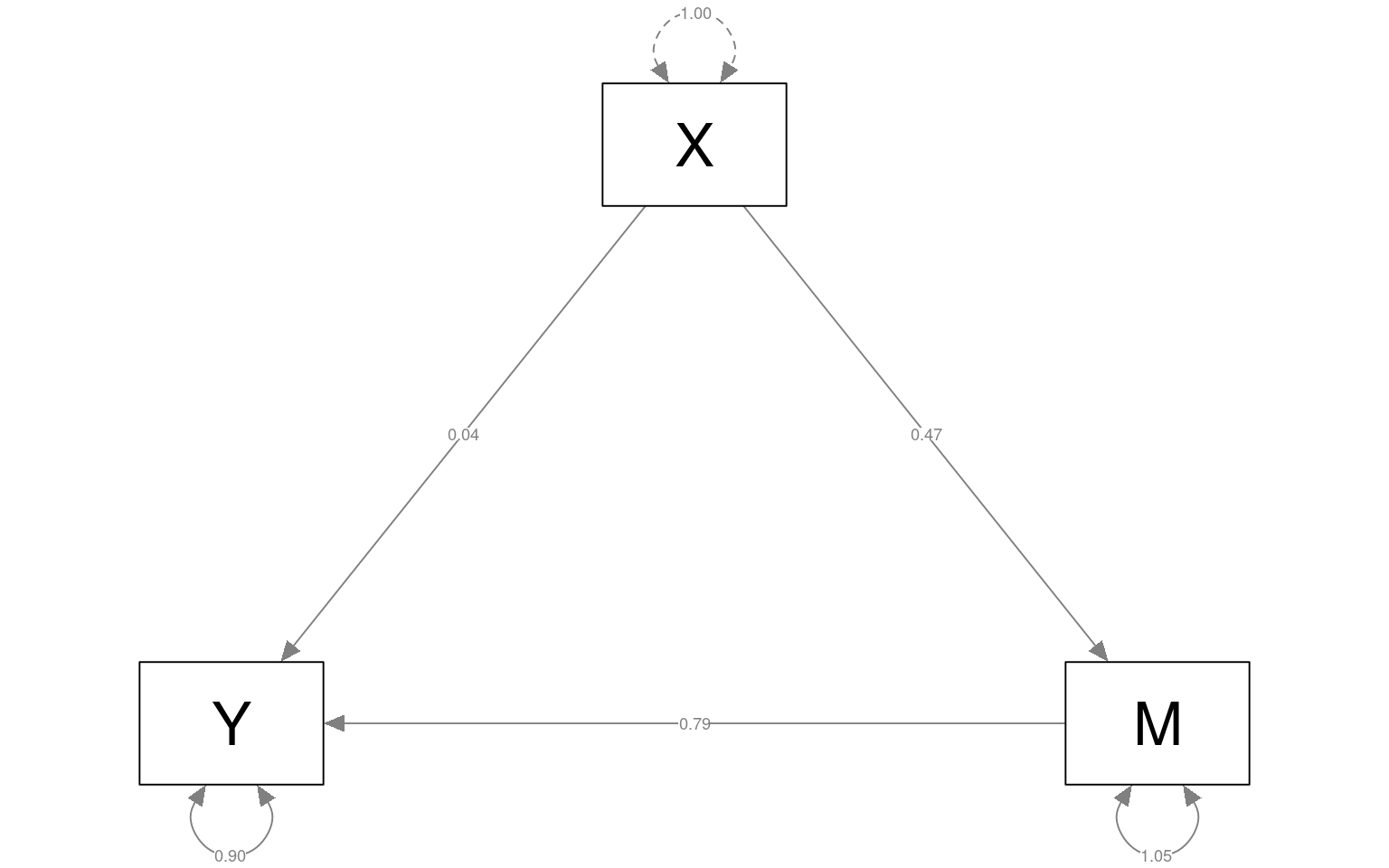
Looking at this first model (where M really mediates X-Y), we see that the edges X-M and M-Y are strong, but X->Y is weak, indicating M mediates the relationship between X and Y. These values are nearly identical (if not exactly the same) to what we obtained in the mediate function, with c=total=.41, but the lavaan model gives more details.
fitmed2 <- sem(model, data = Data2)
summary(fitmed2)lavaan 0.6.13 ended normally after 1 iteration
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Model Test User Model:
Test statistic 0.000
Degrees of freedom 0
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Regressions:
Estimate Std.Err z-value P(>|z|)
Y ~
X (c) 0.594 0.136 4.360 0.000
M ~
X (a) 0.748 0.104 7.227 0.000
Y ~
M (b) -0.097 0.107 -0.910 0.363
Variances:
Estimate Std.Err z-value P(>|z|)
.Y 1.218 0.172 7.071 0.000
.M 1.070 0.151 7.071 0.000
Defined Parameters:
Estimate Std.Err z-value P(>|z|)
ab -0.073 0.080 -0.903 0.367
total 0.521 0.111 4.702 0.000# lavaan.diagram(fit2)
semPaths(fitmed2, curvePilot = T, "par", weighted = FALSE, nCharNodes = 7, shapeMan = "rectangle",
sizeMan = 8, sizeMan2 = 5)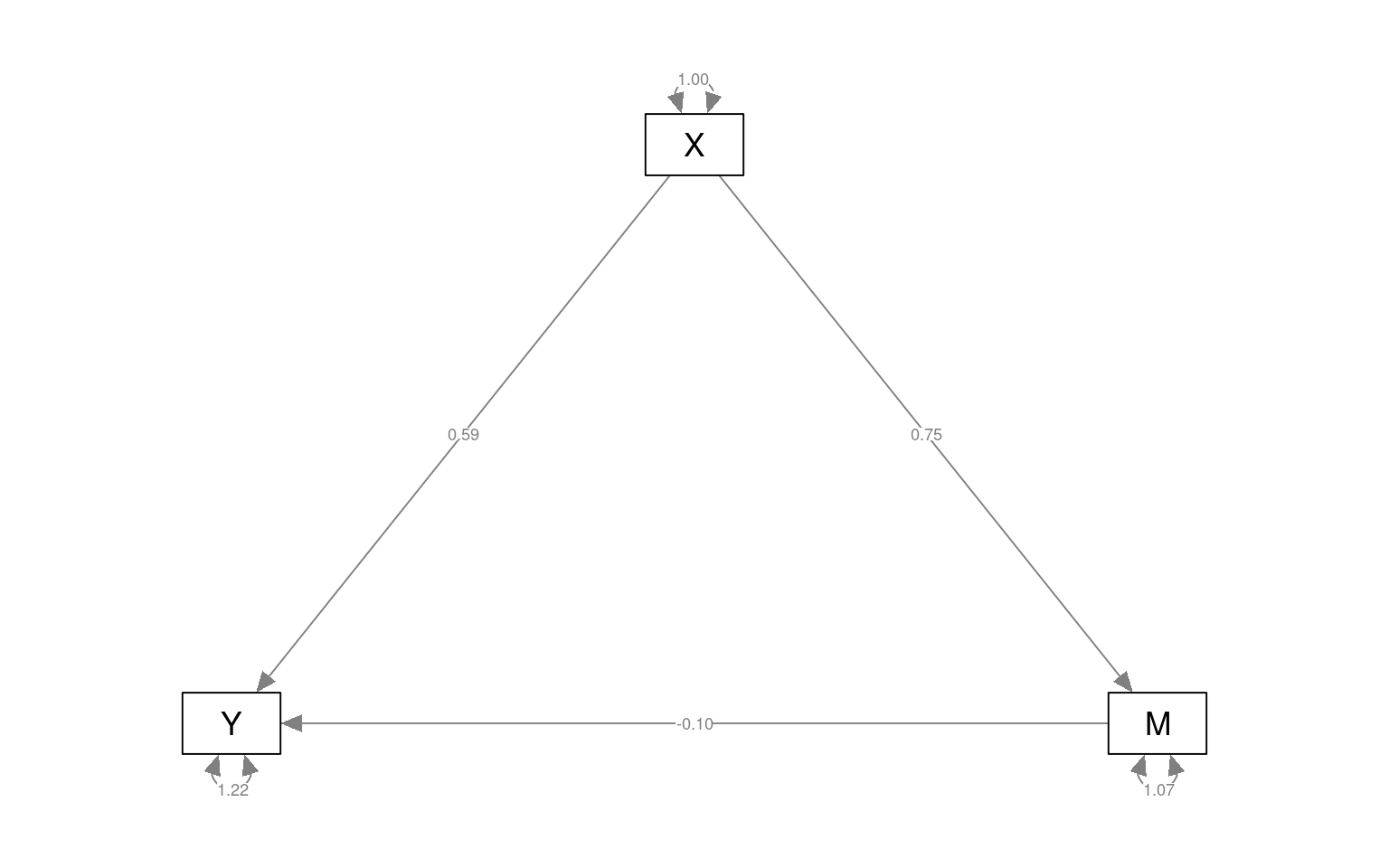
Here, Y-M is not significant, but Y-X and M-X are, indicating that M
does not mediate the relationship. Note that the model is framed to test
whether a particular value is significant–we don’t make two models and
compare theme via ANOVA.
Example:
dat <- read.csv("data_study1.csv")
dat$female <- dat$Gender == "female"
dat$phonenumeric <- dat$Smartphone == "iPhone"
round(cor(dat$phonenumeric, dat[, 3:14])) Age Honesty.Humility Emotionality Extraversion Agreeableness
[1,] 0 0 0 0 0
Conscientiousness Openness Avoidance.Similarity Phone.as.status.object
[1,] 0 0 0 0
Social.Economic.Status Time.owned.current.phone female
[1,] 0 0 0par(mar = c(2, 15, 2, 0))
barplot(abs(cor(dat$phonenumeric, dat[, 3:14])), main = "Correlations with iphone ownership",
horiz = T, las = 1)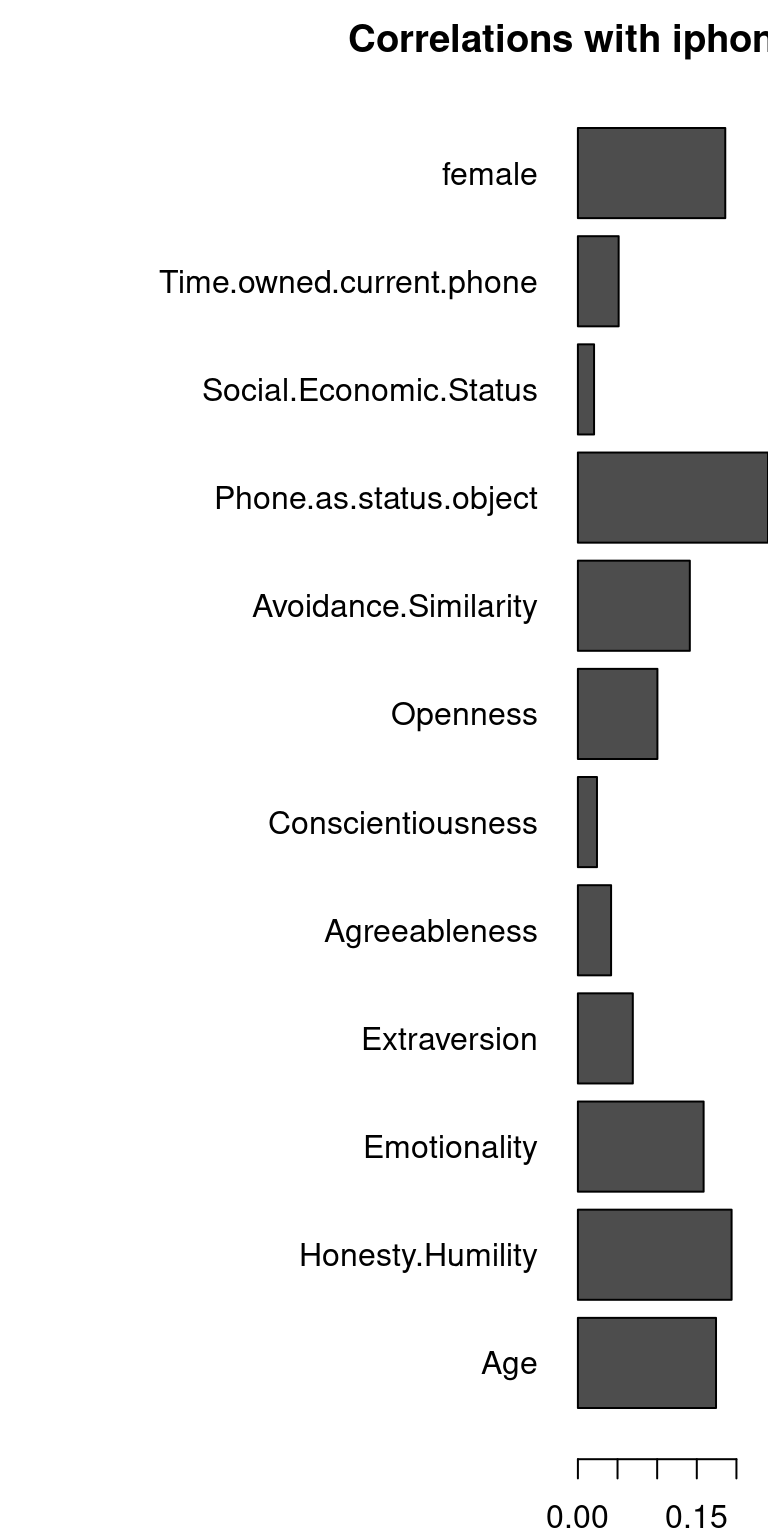
We can see that age and phone-as-status-symbol both correlate with iphone ownership. But are they independent? More importantly, can the effect of age be explained by the effect of status-symbol? I’ll rescale age to be between 0 and 1 to make the coefficients larger–otherwise it doesn’t matter.
dat$Age <- dat$Age/100
psych::mediate(phonenumeric ~ Age + (Phone.as.status.object), data = dat)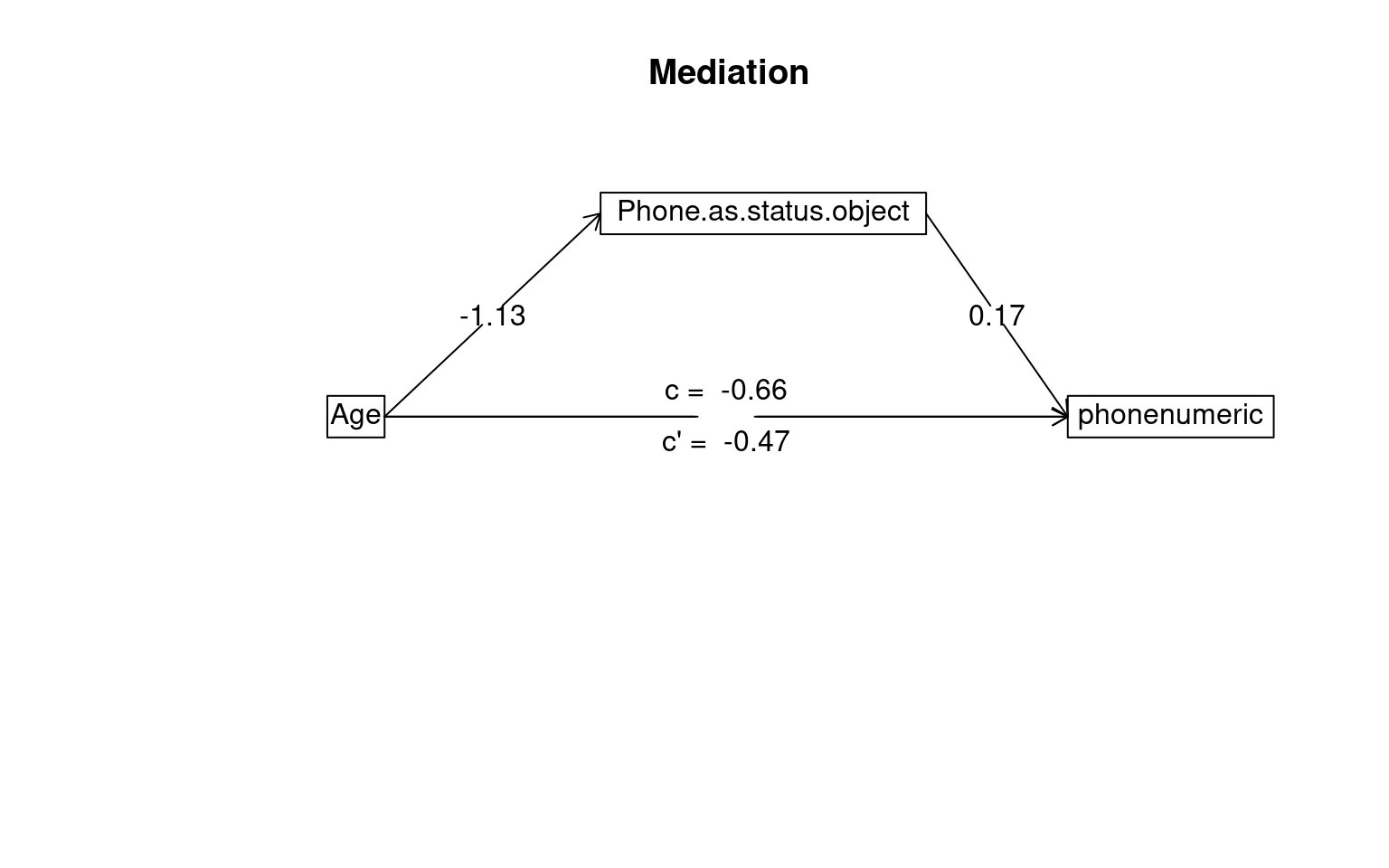
Mediation/Moderation Analysis
Call: psych::mediate(y = phonenumeric ~ Age + (Phone.as.status.object),
data = dat)
The DV (Y) was phonenumeric . The IV (X) was Age . The mediating variable(s) = Phone.as.status.object .
Total effect(c) of Age on phonenumeric = -0.66 S.E. = 0.16 t = -4.06 df= 527 with p = 5.6e-05
Direct effect (c') of Age on phonenumeric removing Phone.as.status.object = -0.47 S.E. = 0.17 t = -2.83 df= 526 with p = 0.0049
Indirect effect (ab) of Age on phonenumeric through Phone.as.status.object = -0.2
Mean bootstrapped indirect effect = -0.2 with standard error = 0.05 Lower CI = -0.3 Upper CI = -0.11
R = 0.27 R2 = 0.07 F = 20.29 on 2 and 526 DF p-value: 1.87e-12
To see the longer output, specify short = FALSE in the print statement or ask for the summaryThe test suggests the indirect effect of age on phone usage through status symbol is statistically significant, but so is the direct effect. This suggests that although some of the impact of age on iphone usage can be explained by younger people being more likely to treat the phone as a status symbol (and those people tend to buy iphones), there is also a effect of age directly–even for people with the same level of phone-as-status-symbol, there is an age effect.
Exercise:
Form a mediation model for other variables within the iphone data.
Correspondence Analysis and Multiple Correspondence Analysis
Correspondance Analysis (CA) and Multiple Correspondence Analysis (MCA) are described as analogs to PCA for categorical variables. For example, it might be useful as an alternative to looking at cross-tabs for categorical variables. It can also be used in concert with inter-rater reliability to establish coding schemes that correspond with one another, or with k-means or other clustering to establish how different solutions correspond.
Resources
- Packages:
ca - corresp() in
MASS - https://www.utdallas.edu/~herve/Abdi-MCA2007-pretty.pdf
- http://gastonsanchez.com/visually-enforced/how-to/2012/10/13/MCA-in-R/
- Nenadic, O. and Greenacre, M. (2007). Correspondence analysis in R, with two- and three-dimensional graphics: The ca package. Journal of Statistical Software, 20 (3), http://www.jstatsoft.org/v20/i03/
Correspondence Analysis (CA) is available with the corresp() in MASS and the ca package, which provides better visualizations.
Background and Example
For CA, The basic problem we have is trying to understand whether two categorical variables have some sort of relationship. The problem is that, unless they are binary, correlation won’t work. One could imagine some sort of matching algorithm, to find how categories best align, and then finding the sum of the diagonals. Another problem is that we may not have the same number of levels of groups–can we come up with some sort of correspondence there? This is similar to the problem we face when looking at clustering solutions and trying to determine how well a solution corresponds to some particular category we used outside of the model. The clusters don’t have labels that will match the secondary variable, but we’d still like to measure how well they did.
Let’s try this with the iris data, and k-means clustering
library(MASS)
set.seed(5220)
iris2 <- scale(iris[, 1:4])
model <- kmeans(iris[, 1:4], centers = 3)
table(iris$Species, model$cluster)
1 2 3
setosa 50 0 0
versicolor 0 2 48
virginica 0 36 14MASS library corresp function
Can we measure how good the correspondence is between our clusters and the true species?
library(MASS)
camodel <- corresp(iris$Species, model$cluster, nf = 2)
print(camodel)First canonical correlation(s): 1.0000000 0.7004728
x scores:
[,1] [,2]
setosa -1.4142136 3.276967e-16
versicolor 0.7071068 1.224745e+00
virginica 0.7071068 -1.224745e+00
y scores:
[,1] [,2]
1 -1.4142136 2.287696e-16
2 0.7071068 -1.564407e+00
3 0.7071068 9.588299e-01plot(camodel)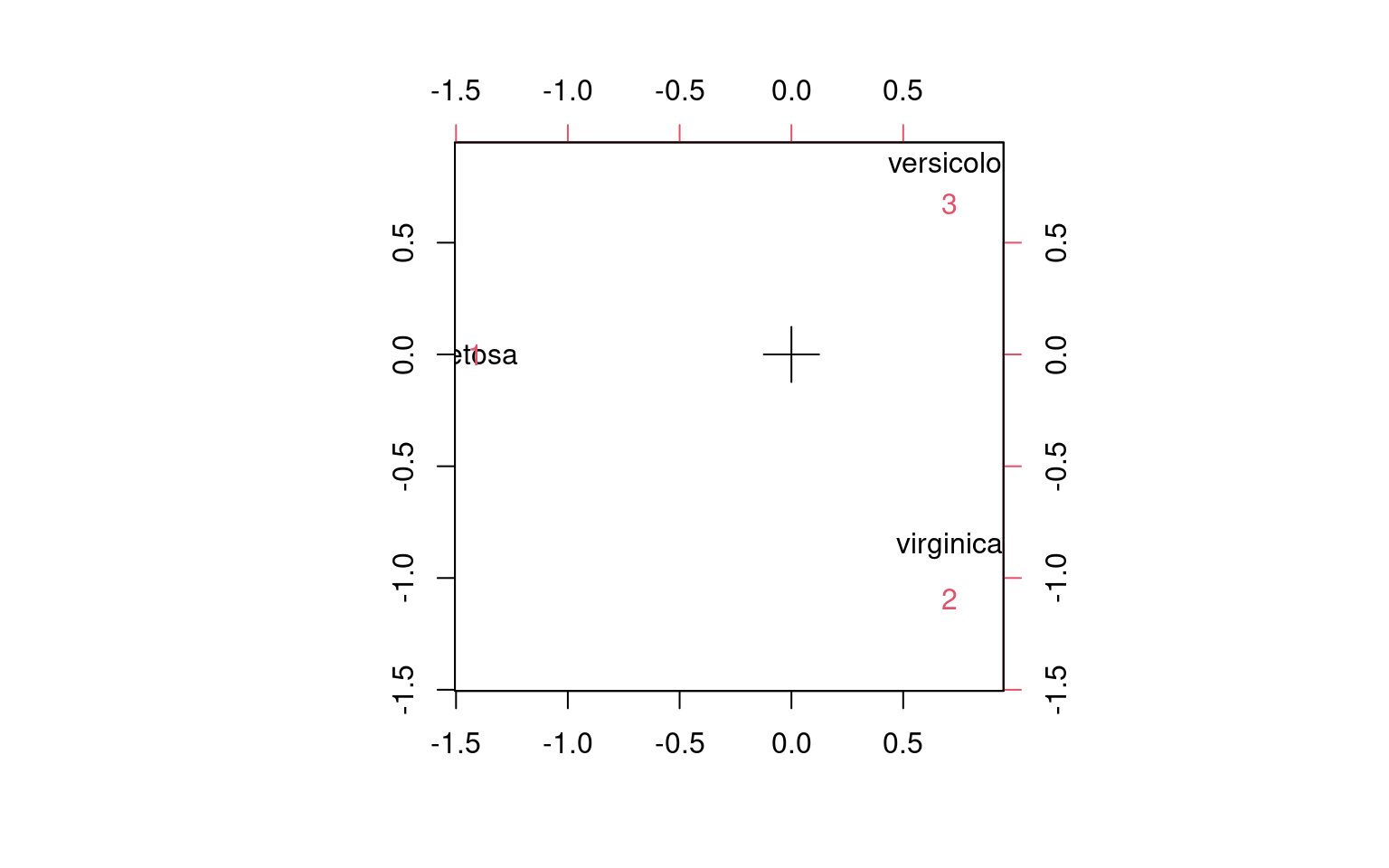
The model can also be specified like this:
tmp <- data.frame(spec = iris$Species, cl = model$cluster)
camodel2 <- corresp(~spec + cl, data = tmp, nf = 2)
camodel2First canonical correlation(s): 1.0000000 0.7004728
spec scores:
[,1] [,2]
setosa -1.4142136 3.276967e-16
versicolor 0.7071068 1.224745e+00
virginica 0.7071068 -1.224745e+00
cl scores:
[,1] [,2]
1 -1.4142136 2.287696e-16
2 0.7071068 -1.564407e+00
3 0.7071068 9.588299e-01ca library ca function
A similar result can be obtained by doing ca on the cross-table.
library(ca)
cmodel3 <- ca::ca(table(iris$Species, model$cluster), nd = 4)
cmodel3
Principal inertias (eigenvalues):
1 2
Value 1 0.490662
Percentage 67.08% 32.92%
Rows:
setosa versicolor virginica
Mass 0.333333 0.333333 0.333333
ChiDist 1.414214 1.111752 1.111752
Inertia 0.666667 0.411998 0.411998
Dim. 1 -1.414214 0.707107 0.707107
Dim. 2 0.000000 -1.224745 1.224745
Columns:
1 2 3
Mass 0.333333 0.253333 0.413333
ChiDist 1.414214 1.304159 0.975240
Inertia 0.666667 0.430877 0.393118
Dim. 1 -1.414214 0.707107 0.707107
Dim. 2 0.000000 1.564407 -0.958830summary(cmodel3)
Principal inertias (eigenvalues):
dim value % cum% scree plot
1 10000000 67.1 67.1 *****************
2 0.490662 32.9 100.0 ********
-------- -----
Total: 1.490662 100.0
Rows:
name mass qlt inr k=1 cor ctr k=2 cor ctr
1 | sets | 333 1000 447 | -1414 1000 667 | 0 0 0 |
2 | vrsc | 333 1000 276 | 707 405 167 | -858 595 500 |
3 | vrgn | 333 1000 276 | 707 405 167 | 858 595 500 |
Columns:
name mass qlt inr k=1 cor ctr k=2 cor ctr
1 | 1 | 333 1000 447 | -1414 1000 667 | 0 0 0 |
2 | 2 | 253 1000 289 | 707 294 127 | 1096 706 620 |
3 | 3 | 413 1000 264 | 707 526 207 | -672 474 380 |plot(cmodel3)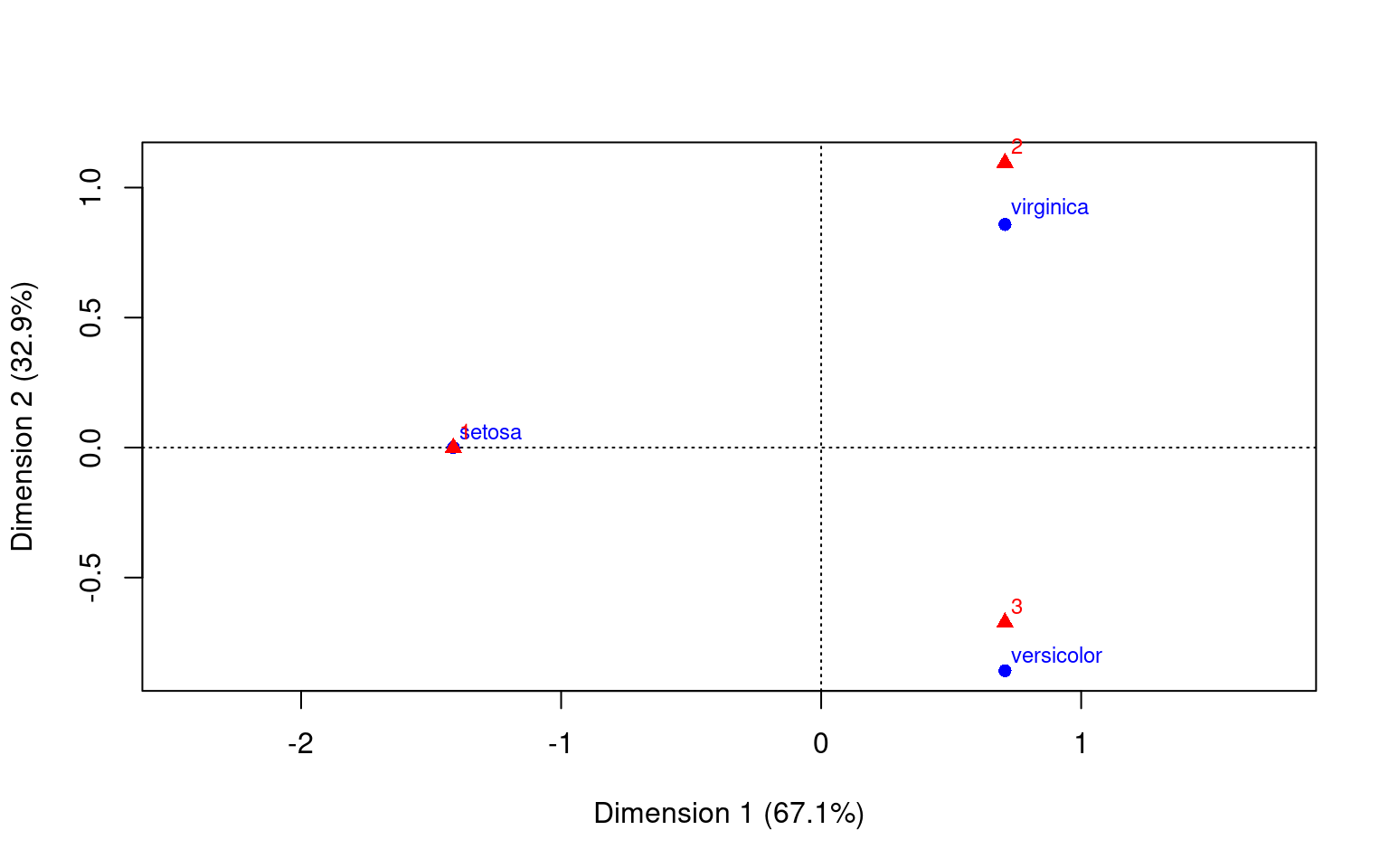
We can see that using any of these methods, we have mapped the categories into a space of principal components–using SVD. Furthermore it places both the ‘rows’ and ‘columns’ into that space, so we can see how closely aligned the groups are. We chose to use 2 dimensions in each case for easy visualization. What if the correspondence is not as good?
set.seed(1001)
iris2 <- scale(iris[, 1:4])
model <- kmeans(iris[, 1:4], centers = 5)
table(iris$Species, model$cluster)
1 2 3 4 5
setosa 0 0 50 0 0
versicolor 21 27 0 2 0
virginica 0 1 0 27 22cmodel5 <- ca(table(iris$Species, model$cluster), nd = 2)cmodel5
Principal inertias (eigenvalues):
1 2
Value 1 0.886946
Percentage 53% 47%
Rows:
setosa versicolor virginica
Mass 0.333333 0.333333 0.333333
ChiDist 1.414214 1.352930 1.352930
Inertia 0.666667 0.610140 0.610140
Dim. 1 -1.414214 0.707107 0.707107
Dim. 2 0.000000 -1.224745 1.224745
Columns:
1 2 3 4 5
Mass 0.140000 0.186667 0.333333 0.193333 0.146667
ChiDist 1.414214 1.339167 1.414214 1.270726 1.414214
Inertia 0.280000 0.334762 0.666667 0.312184 0.293333
Dim. 1 0.707107 0.707107 -1.414214 0.707107 0.707107
Dim. 2 -1.300460 -1.207570 0.000000 1.121086 1.300460plot(cmodel5)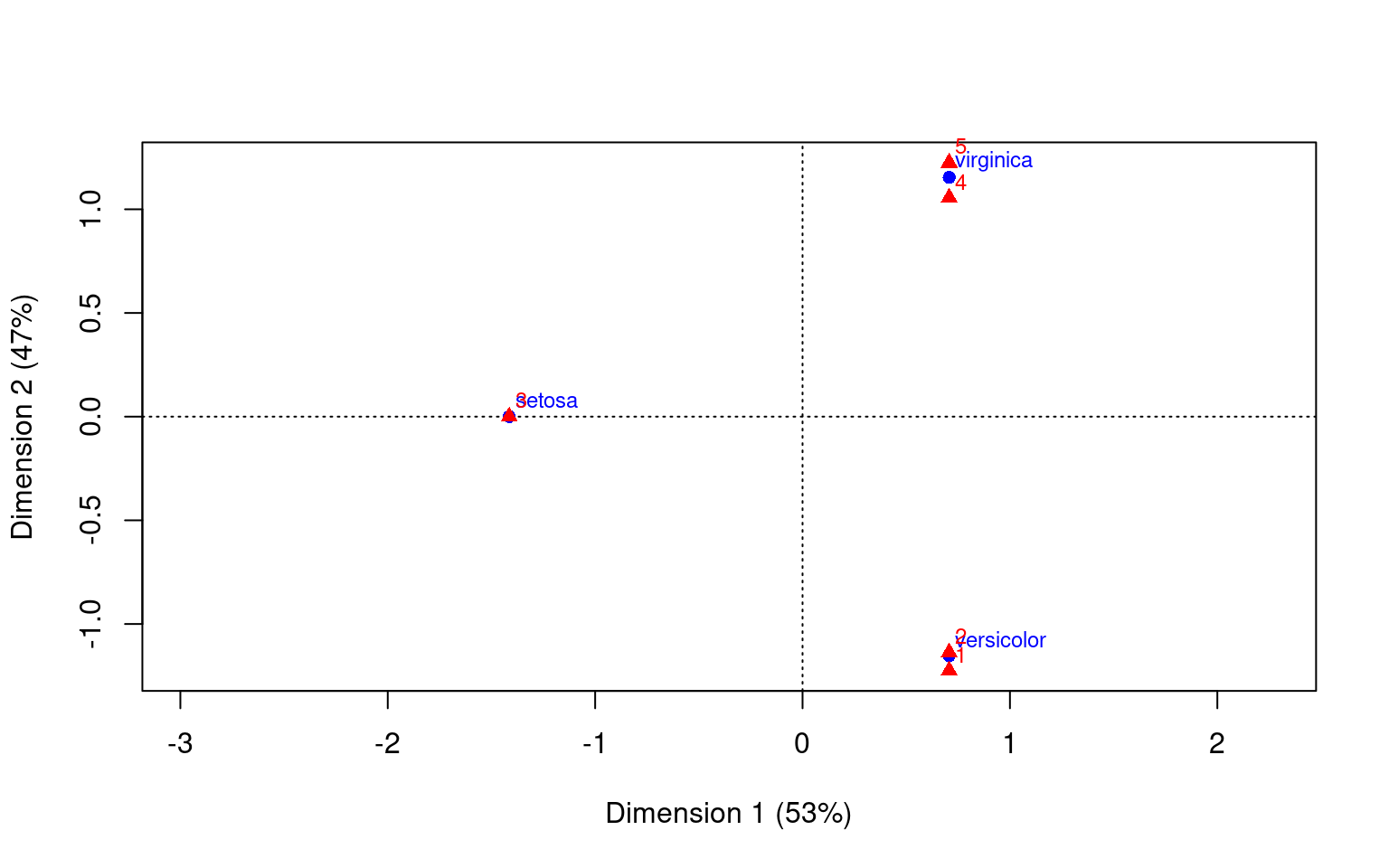
This should match our intuition for where the two sets of labels
belong.
Other Examples (from ca help file)
This data sets maps the distribution of letters of the alphabet to authors. These dimensions might be used to detect language, style, historic period, or something
data("author")
ca(author)
Principal inertias (eigenvalues):
1 2 3 4 5 6 7
Value 0.007664 0.003688 0.002411 0.001383 0.001002 0.000723 0.000659
Percentage 40.91% 19.69% 12.87% 7.38% 5.35% 3.86% 3.52%
8 9 10 11
Value 0.000455 0.000374 0.000263 0.000113
Percentage 2.43% 2% 1.4% 0.6%
Rows:
three daughters (buck) drifters (michener) lost world (clark)
Mass 0.085407 0.079728 0.084881
ChiDist 0.097831 0.094815 0.128432
Inertia 0.000817 0.000717 0.001400
Dim. 1 -0.095388 0.405697 1.157803
Dim. 2 -0.794999 -0.405560 -0.023114
east wind (buck) farewell to arms (hemingway)
Mass 0.089411 0.082215
ChiDist 0.118655 0.122889
Inertia 0.001259 0.001242
Dim. 1 -0.173901 -0.831886
Dim. 2 0.434443 -0.136485
sound and fury 7 (faulkner) sound and fury 6 (faulkner)
Mass 0.082310 0.083338
ChiDist 0.172918 0.141937
Inertia 0.002461 0.001679
Dim. 1 0.302025 -0.925572
Dim. 2 2.707599 0.966944
profiles of future (clark) islands (hemingway) pendorric 3 (holt)
Mass 0.089722 0.082776 0.079501
ChiDist 0.187358 0.165529 0.113174
Inertia 0.003150 0.002268 0.001018
Dim. 1 1.924060 -1.566481 -0.724758
Dim. 2 -0.249310 -1.185338 -0.106349
asia (michener) pendorric 2 (holt)
Mass 0.077827 0.082884
ChiDist 0.155115 0.101369
Inertia 0.001873 0.000852
Dim. 1 1.179548 -0.764937
Dim. 2 -1.186934 -0.091188
Columns:
a b c d e f g
Mass 0.079847 0.015685 0.022798 0.045967 0.127070 0.019439 0.020025
ChiDist 0.048441 0.148142 0.222783 0.189938 0.070788 0.165442 0.156640
h i j k l m n
Mass 0.064928 0.070092 0.000789 0.009181 0.042667 0.025500 0.068968
ChiDist 0.154745 0.086328 0.412075 0.296727 0.120397 0.159747 0.075706
o p q r s t u
Mass 0.076572 0.015159 0.000669 0.051897 0.060660 0.093010 0.029756
ChiDist 0.088101 0.250617 0.582298 0.111725 0.123217 0.050630 0.119215
v w x y z
Mass 0.009612 0.025847 0.001160 0.021902 0.000801
ChiDist 0.269770 0.232868 0.600831 0.301376 0.833700
[ reached getOption("max.print") -- omitted 3 rows ]plot(ca(author))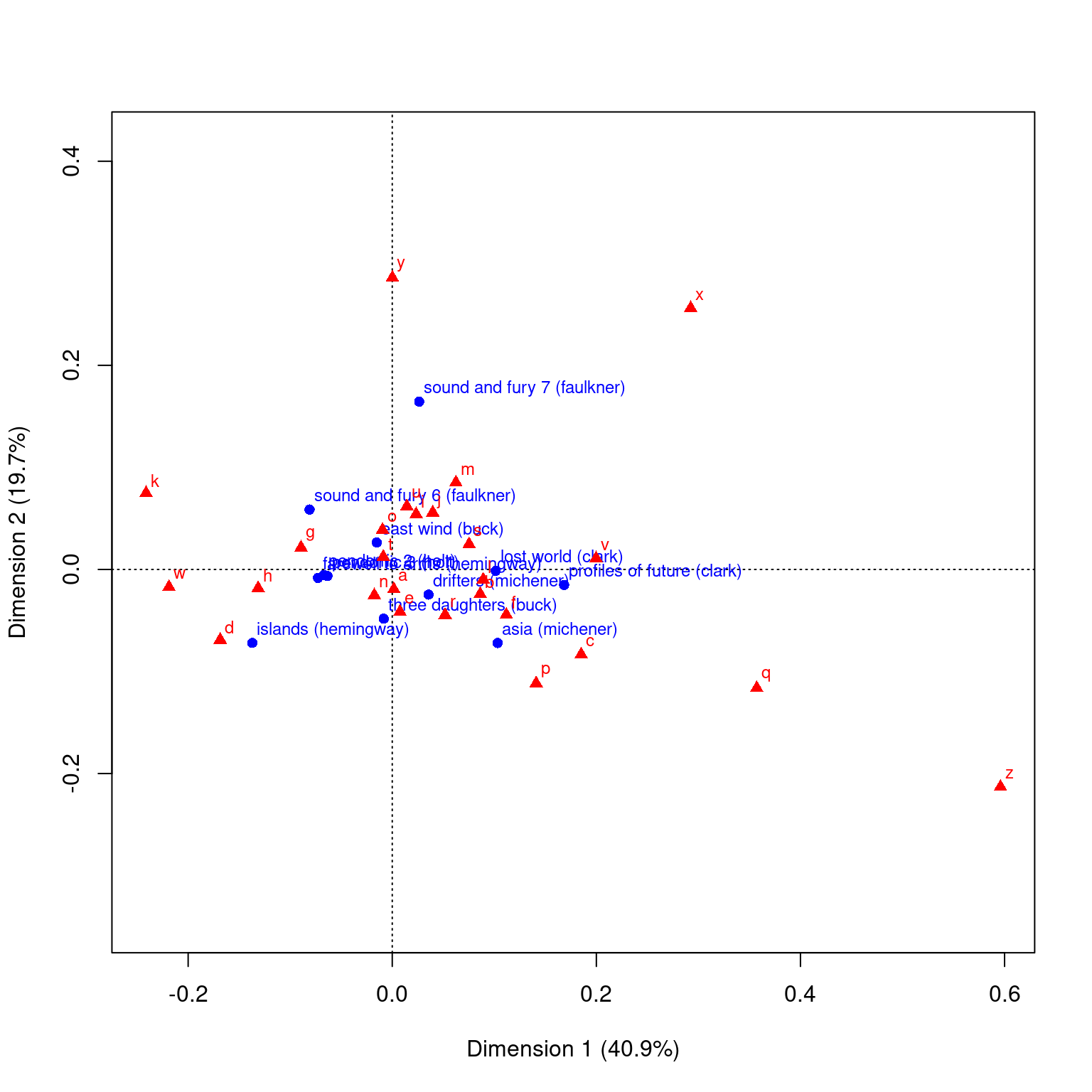
plot(ca(author), what = c("none", "all"))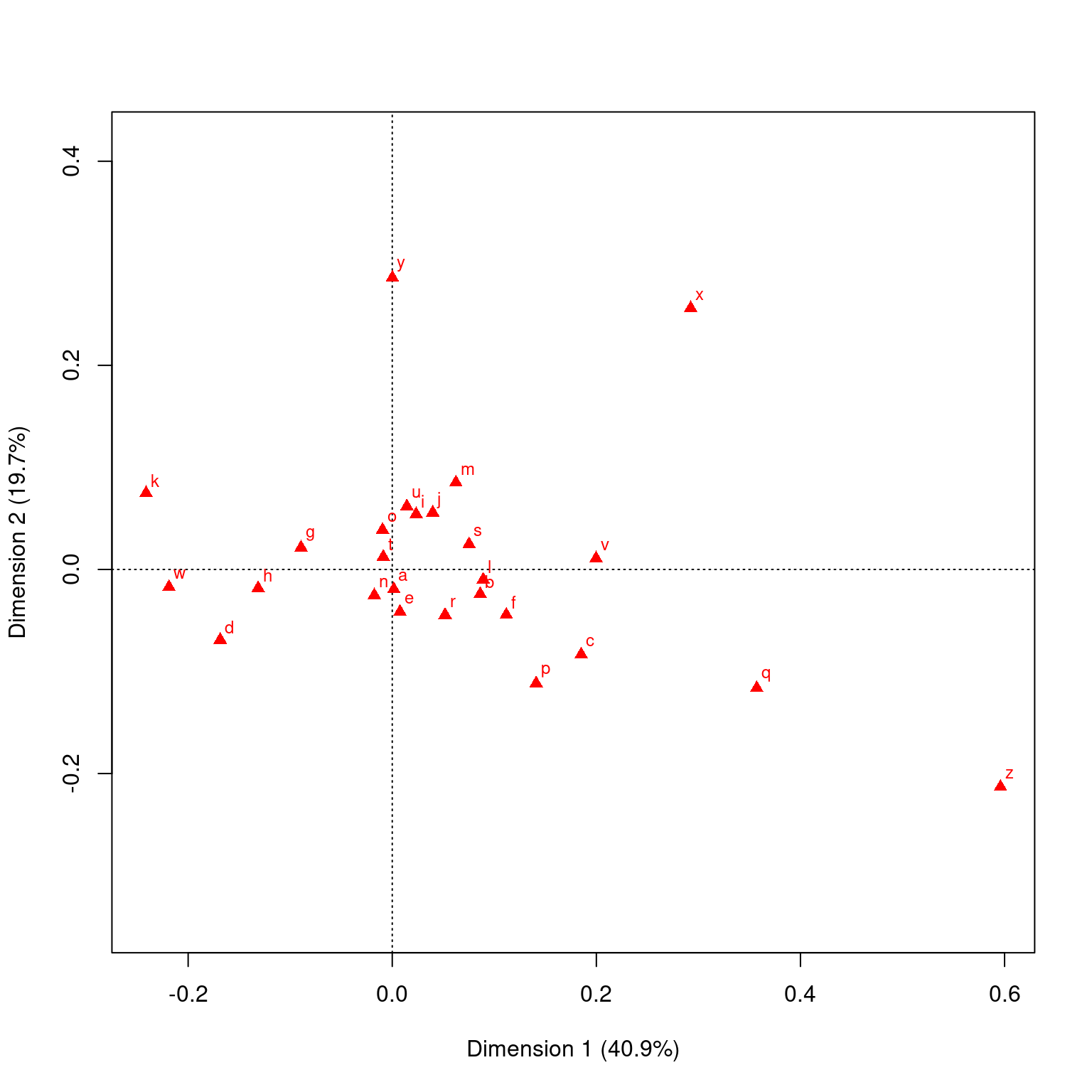
plot(ca(author), what = c("all", "none"))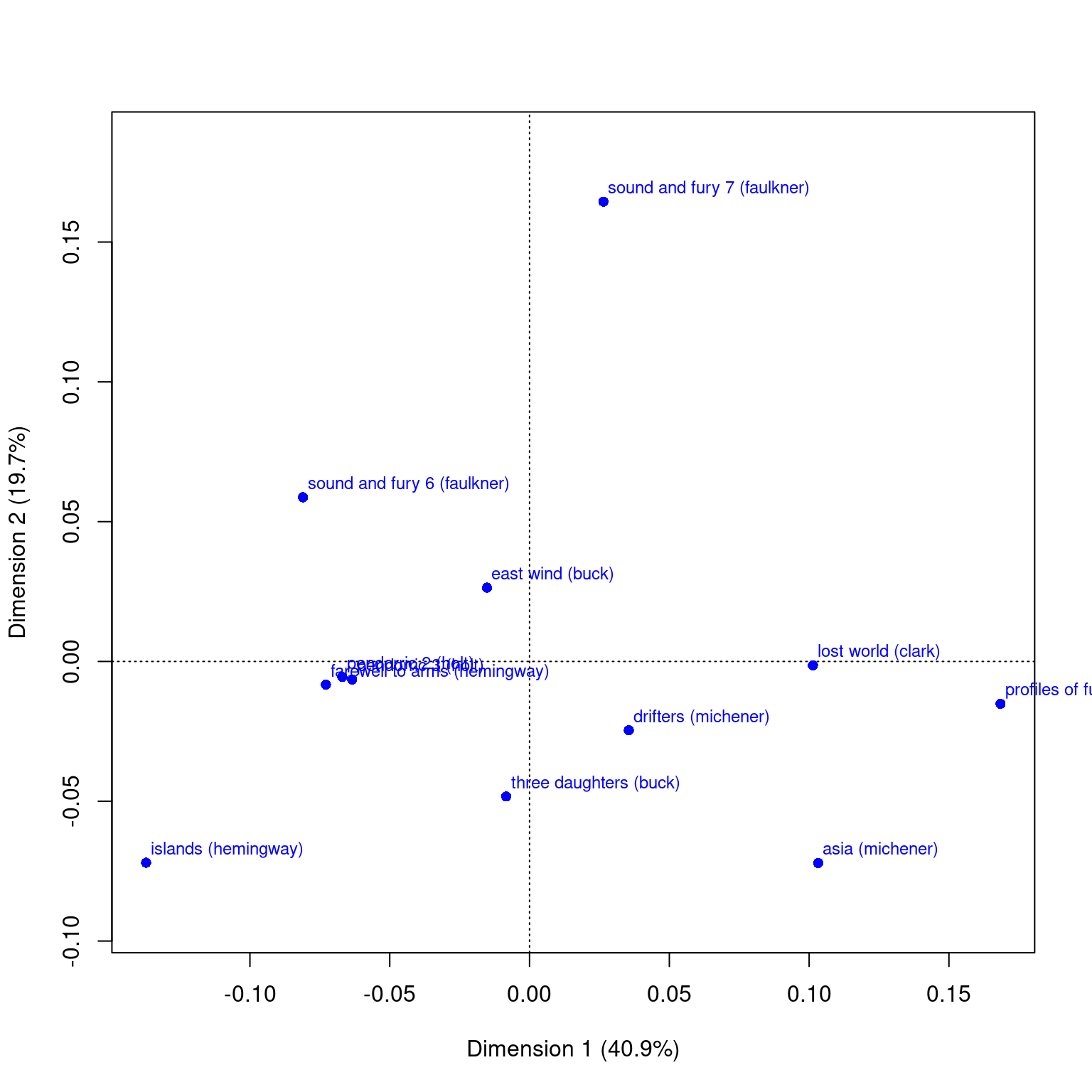
# table method
haireye <- margin.table(HairEyeColor, 1:2)
haireye.ca <- ca(haireye)
haireye.ca
Principal inertias (eigenvalues):
1 2 3
Value 0.208773 0.022227 0.002598
Percentage 89.37% 9.52% 1.11%
Rows:
Black Brown Red Blond
Mass 0.182432 0.483108 0.119932 0.214527
ChiDist 0.551192 0.159461 0.354770 0.838397
Inertia 0.055425 0.012284 0.015095 0.150793
Dim. 1 -1.104277 -0.324463 -0.283473 1.828229
Dim. 2 1.440917 -0.219111 -2.144015 0.466706
Columns:
Brown Blue Hazel Green
Mass 0.371622 0.363176 0.157095 0.108108
ChiDist 0.500487 0.553684 0.288654 0.385727
Inertia 0.093086 0.111337 0.013089 0.016085
Dim. 1 -1.077128 1.198061 -0.465286 0.354011
Dim. 2 0.592420 0.556419 -1.122783 -2.274122plot(haireye.ca)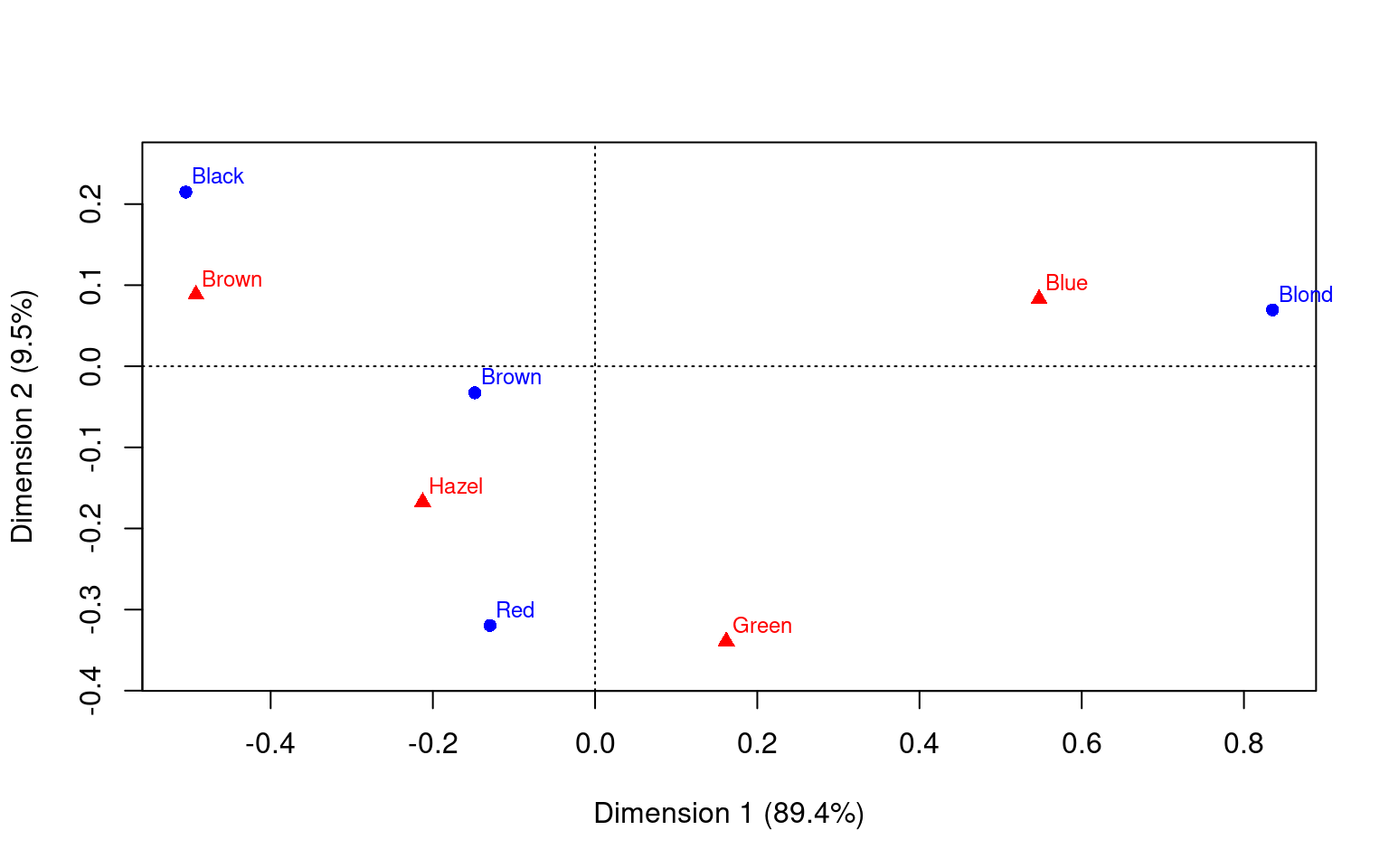
# some plot options
plot(haireye.ca, lines = TRUE)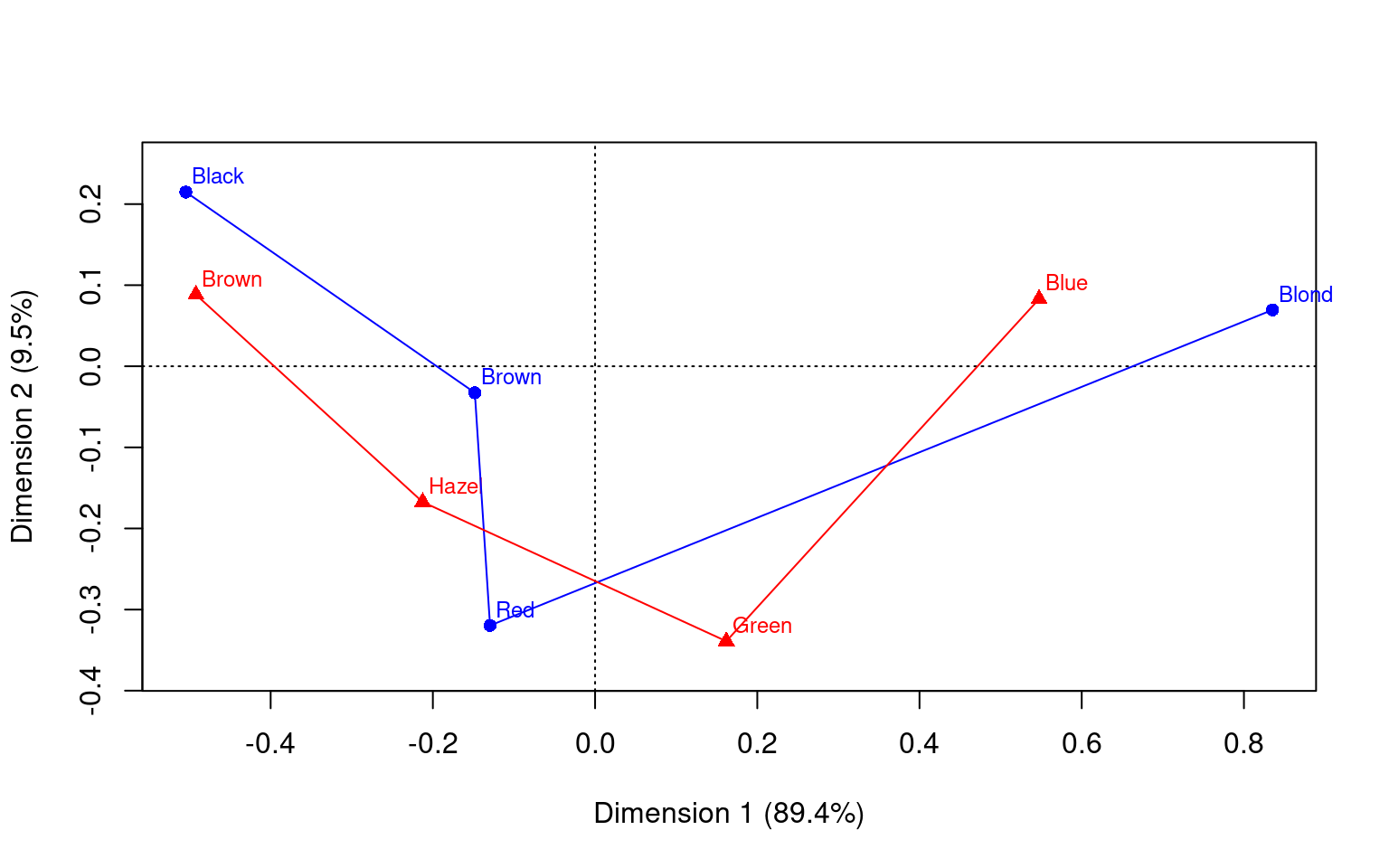
plot(haireye.ca, arrows = c(TRUE, FALSE))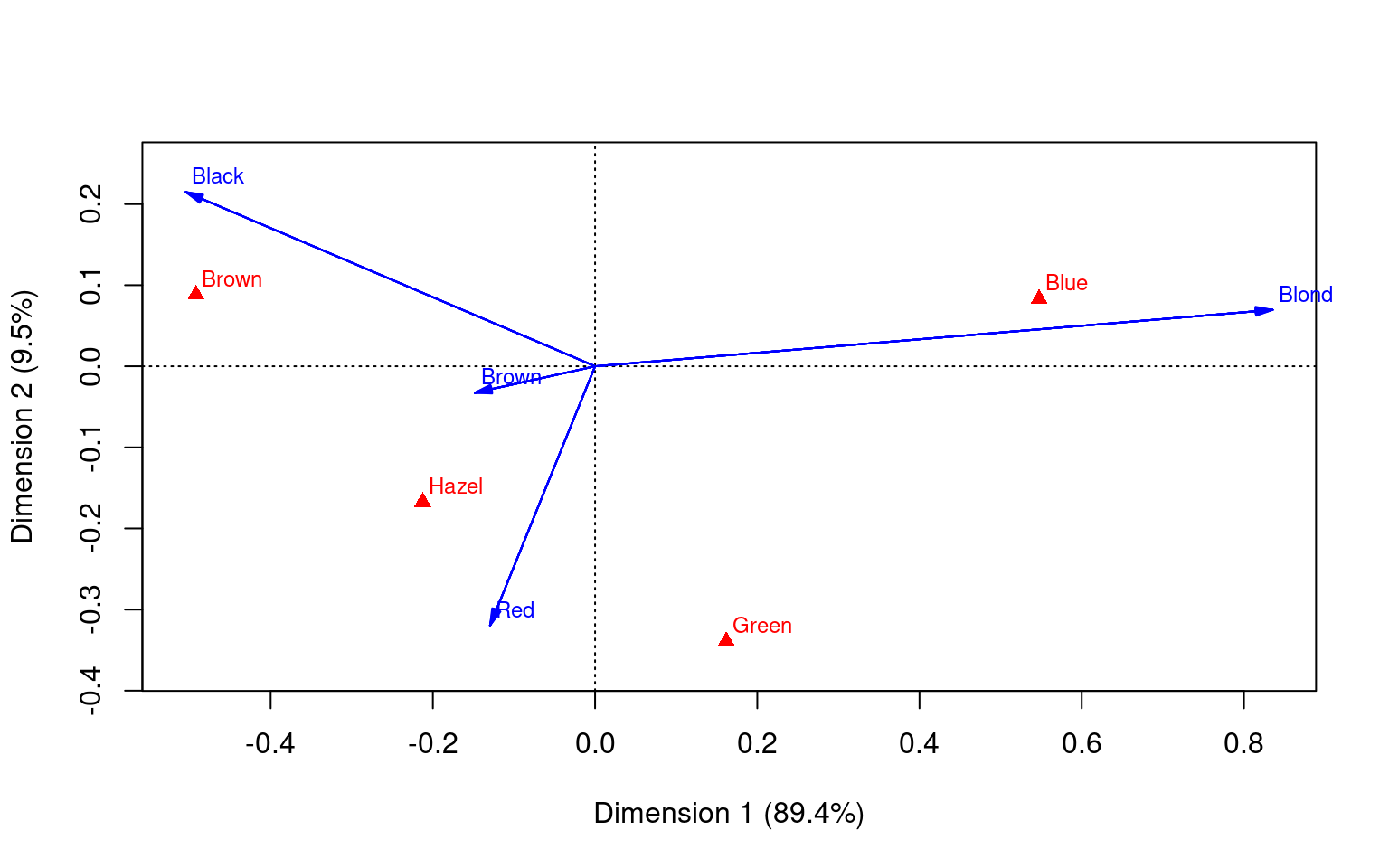
Multiple Correspondence Analysis
We have looked at a pair of variables, often as a contingency table, using CA. But what if you had a large number of measures that were all categorical–like a multiple-choice test. We could maybe adapt CA to tell us things more like factor analysis does for large-scale tests. In general, MCA will take the NxMxO contingency table and use SVD to map each all the dimensions into a single space, showing you where the levels of each dimension fall. Let’s look at the Titanic survivor data set. Was it true that it was ‘women and children first?’ Who survived? Who didn’t?
print(Titanic), , Age = Child, Survived = No
Sex
Class Male Female
1st 0 0
2nd 0 0
3rd 35 17
Crew 0 0
, , Age = Adult, Survived = No
Sex
Class Male Female
1st 118 4
2nd 154 13
3rd 387 89
Crew 670 3
, , Age = Child, Survived = Yes
Sex
Class Male Female
1st 5 1
2nd 11 13
3rd 13 14
Crew 0 0
, , Age = Adult, Survived = Yes
Sex
Class Male Female
1st 57 140
2nd 14 80
3rd 75 76
Crew 192 20titanicmodel <- mjca(Titanic)
print(titanicmodel)
Eigenvalues:
1 2 3
Value 0.067655 0.005386 0
Percentage 76.78% 6.11% 0%
Columns:
Class:1st Class:2nd Class:3rd Class:Crew Sex:Female Sex:Male Age:Adult
Mass 0.036915 0.032372 0.080191 0.100522 0.053385 0.196615 0.237619
ChiDist 1.277781 1.316778 0.749611 0.667164 1.126763 0.305938 0.118369
Inertia 0.060272 0.056129 0.045061 0.044743 0.067777 0.018403 0.003329
Dim. 1 1.726678 0.976191 0.195759 -1.104622 2.360505 -0.640923 -0.101670
Dim. 2 -2.229588 0.457212 1.937417 -0.874018 0.016164 -0.004389 -0.277601
Age:Child Survived:No Survived:Yes
Mass 0.012381 0.169241 0.080759
ChiDist 2.271810 0.394352 0.826420
Inertia 0.063898 0.026319 0.055156
Dim. 1 1.951309 -0.763670 1.600378
Dim. 2 5.327911 0.344441 -0.721825plot(titanicmodel)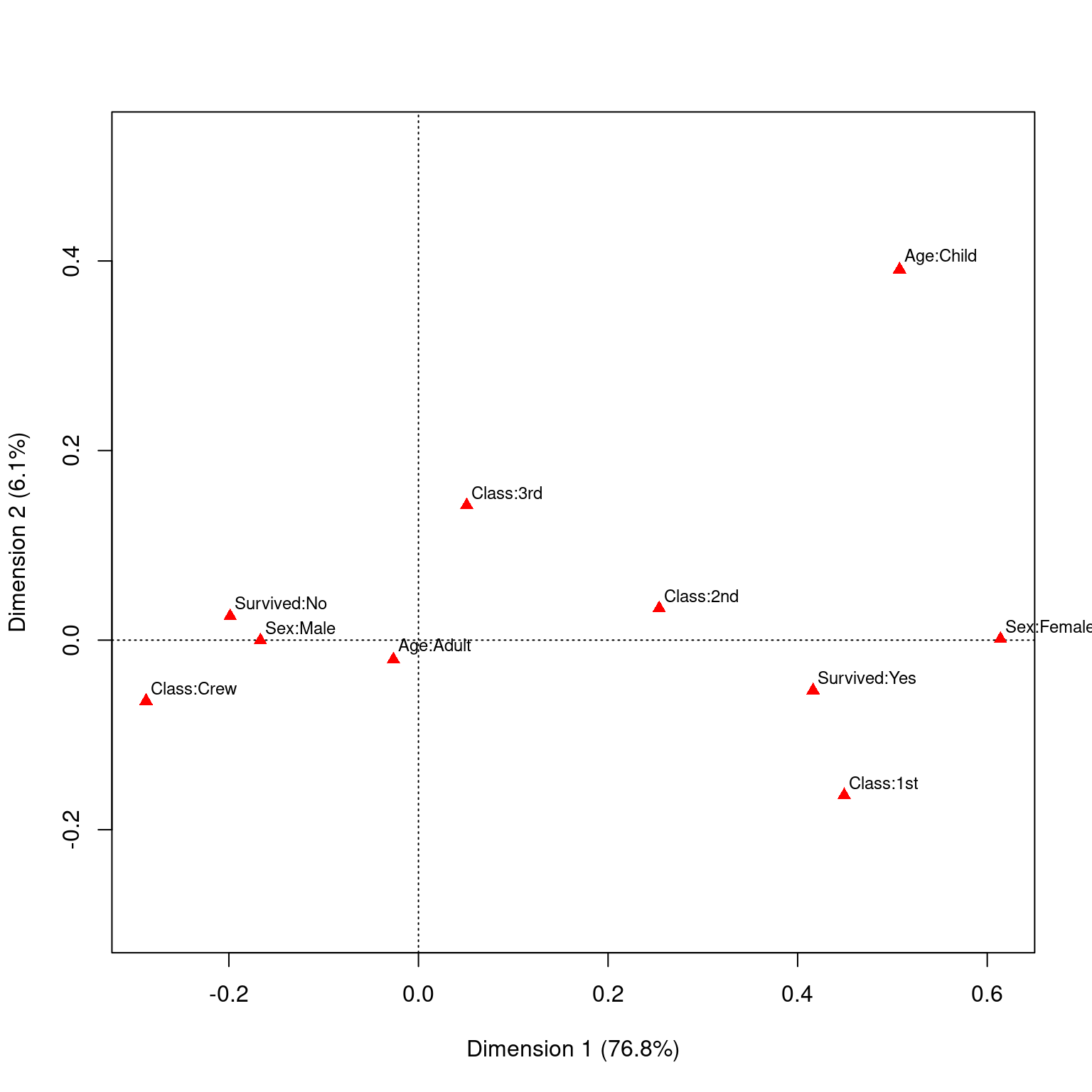
Application: Card-sorting and survey data
The following data set involves a card-sort exercise, which is a common way of understanding users mental models. In this data set collected by Natasha Hardy as part of her dissertation at MTU, A set of 43 topics related to financial planning for retirement were sorted into groups by participants. Each participant could form any group they wanted, and then groups were labelled–but each participant may have used a different sorting. Let’s first look at these as a dissimilarity measure and do some clustering and MDS plotting.
library(MASS)
data <- read.csv("natasha_data.csv")
tab1 <- table(data$participant, data$card.label, data$category.label)
mat <- matrix(0, dim(tab1)[2], dim(tab1)[2])
rownames(mat) <- colnames(mat) <- rownames(tab1[1, , ])
for (sub in 1:dim(tab1)[1]) {
t1 <- tab1[sub, , ]
byindex <- apply(t1, 1, function(x) {
which(x == 1)
})
submat <- outer(byindex, byindex, "==")
mat <- mat + submat
}
rownames(mat) [1] "2008 recession"
[2] "Account management"
[3] "Advice"
[4] "Analyze info"
[5] "Benefits of computers"
[6] "Boomer mentality"
[7] "Casual computer user"
[8] "Confidence"
[9] "Contribution decision"
[10] "Distrust"
[11] "Future orientation"
[12] "Gen X life concept"
[13] "Goals"
[14] "Hardship"
[15] "Health insurance"
[16] "Importance of computers"
[17] "Information availability"
[18] "Intrinsic motivation to learn computers"
[19] "Keeping up computer skills"
[20] "Lack of awareness"
[21] "Learn computers for work"
[22] "Methods for learning computer skills"
[23] "Millennial mentality"
[24] "No discretionary income"
[25] "Parental influence"
[26] "Patience"
[27] "Plan selection"
[28] "Reason for not investing"
[29] "Reason for starting"
[30] "Research"
[31] "Retirement knowledge"
[32] "Retirement lifestyle"
[33] "Retirement planning"
[34] "Risk"
[35] "Self-rated computer skill"
[36] "Serious computer user"
[37] "Social Security"
[38] "Taxes"
[39] "Type of investment"
[40] "Uncertainty"
[41] "Use computers for retirement"
[42] "Withdrawal"
[43] "Worry" look at a clustering
library(cluster)
a <- agnes(12 - mat)
plot(a, which = 2)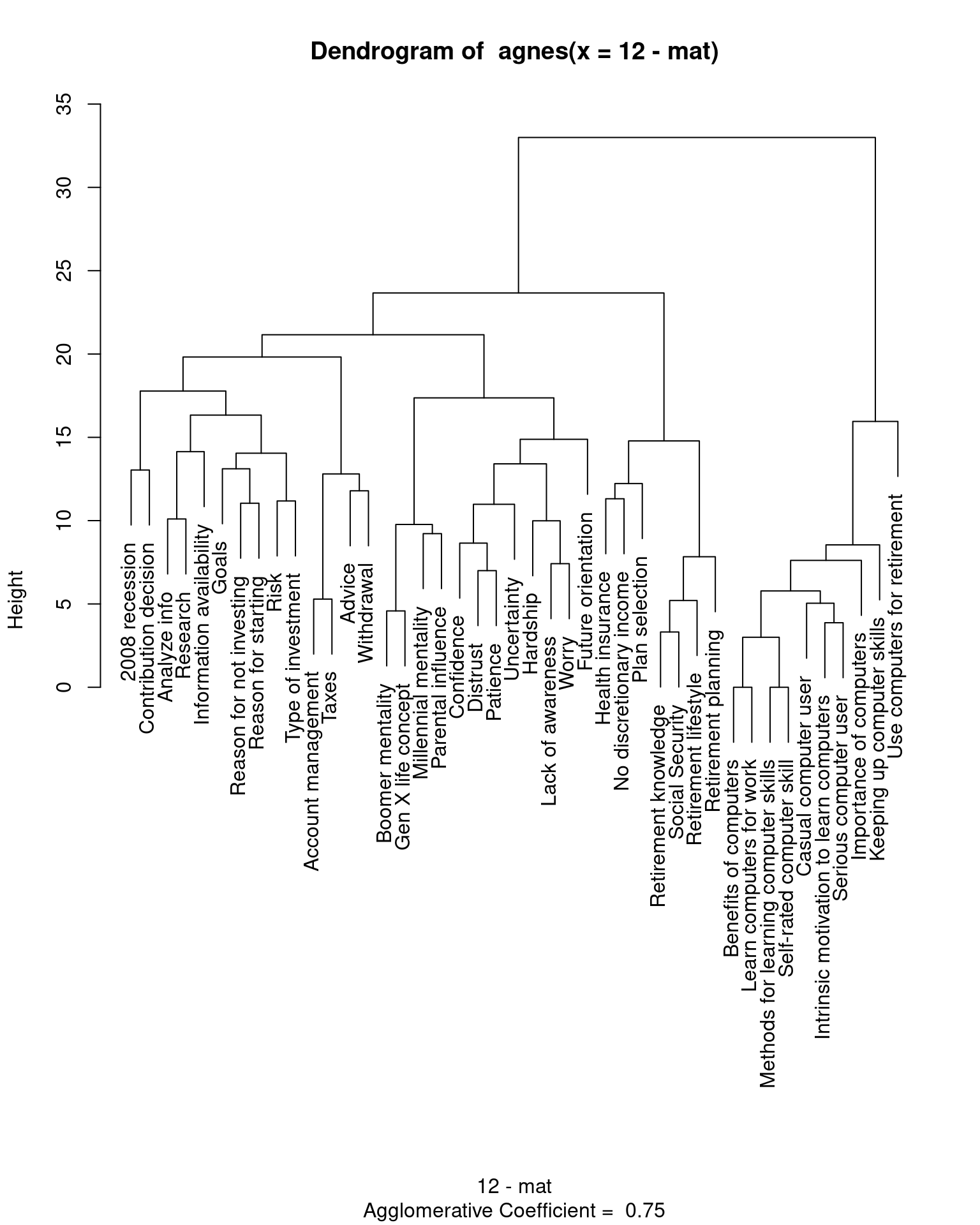
K-means cluster
km <- kmeans(12 - mat, centers = 4)
km$cluster 2008 recession Account management
2 2
Advice Analyze info
2 2
Benefits of computers Boomer mentality
3 4
Casual computer user Confidence
3 4
Contribution decision Distrust
1 4
Future orientation Gen X life concept
4 4
Goals Hardship
2 4
Health insurance Importance of computers
1 3
Information availability Intrinsic motivation to learn computers
2 3
Keeping up computer skills Lack of awareness
3 4
Learn computers for work Methods for learning computer skills
3 3
Millennial mentality No discretionary income
4 1
Parental influence Patience
4 4
Plan selection Reason for not investing
1 2
Reason for starting Research
2 2
Retirement knowledge Retirement lifestyle
1 1
Retirement planning Risk
1 2
Self-rated computer skill Serious computer user
3 3
Social Security Taxes
1 2
Type of investment Uncertainty
2 4
Use computers for retirement Withdrawal
3 2
Worry
4 mds <- isoMDS(12 - mat, k = 2)initial value 31.345692
iter 5 value 26.590630
iter 10 value 25.497491
iter 15 value 24.966145
iter 20 value 24.547825
iter 25 value 23.887370
iter 30 value 23.520014
final value 23.346122
convergedplot(mds$points[, 1], mds$points[, 2], type = "n")
text(mds$points[, 1], mds$points[, 2], rownames(mat), col = km$cluster)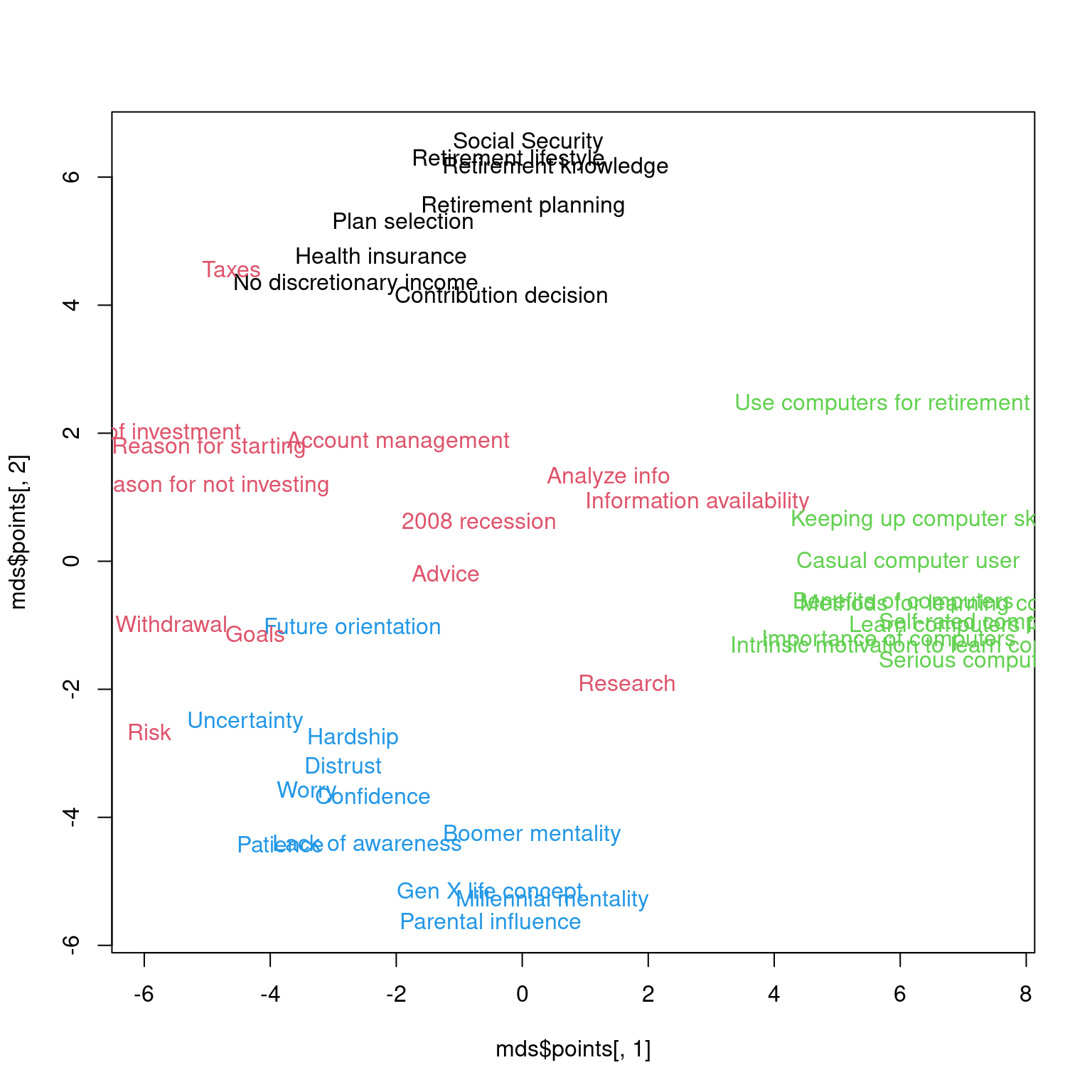
Correspondence analysis
Because each participant labeled the groupings, we can also do a CA. Here, two levels of variables will have some correspondence, and we can use CA to map these into a common vector space.
library(ca)
ca <- ca(table(as.factor(data$card.label), as.factor(data$category.label)))
plot(ca, arrows = c(F, T), xlim = c(-2, 2))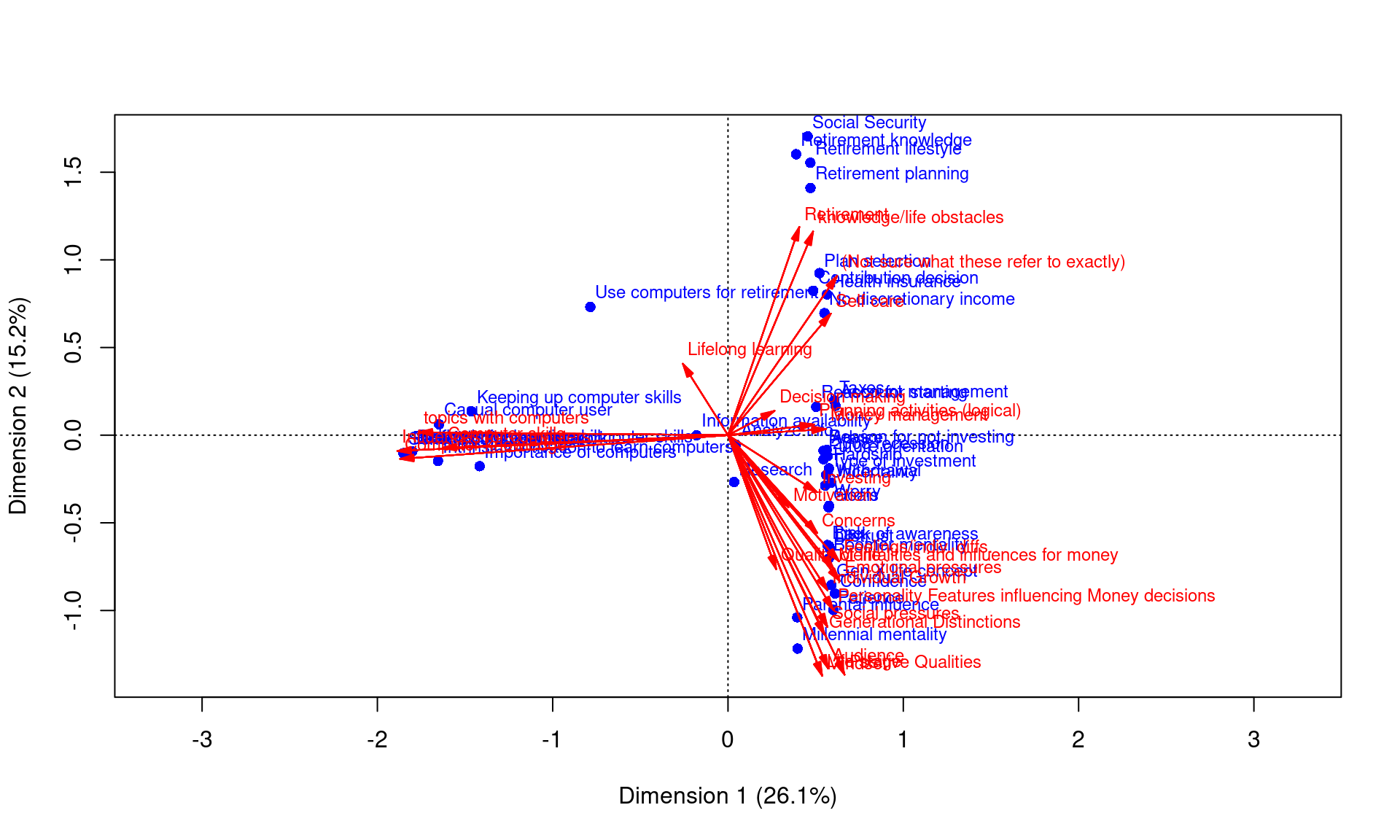
par(mfrow = c(1, 2))
plot.ca(ca, dim = c(1, 2), what = c("none", "all"), main = "Cluster names", xlim = c(-2,
2))
# points(ca$rowcoord[,1], ca$rowcoord[,2],col=km$cluster,pch=16)
plot(ca, dim = c(1, 2), what = c("all", "none"), main = "Sorted topics", xlim = c(-2,
2), col = c("black", "orange"), pch = 1)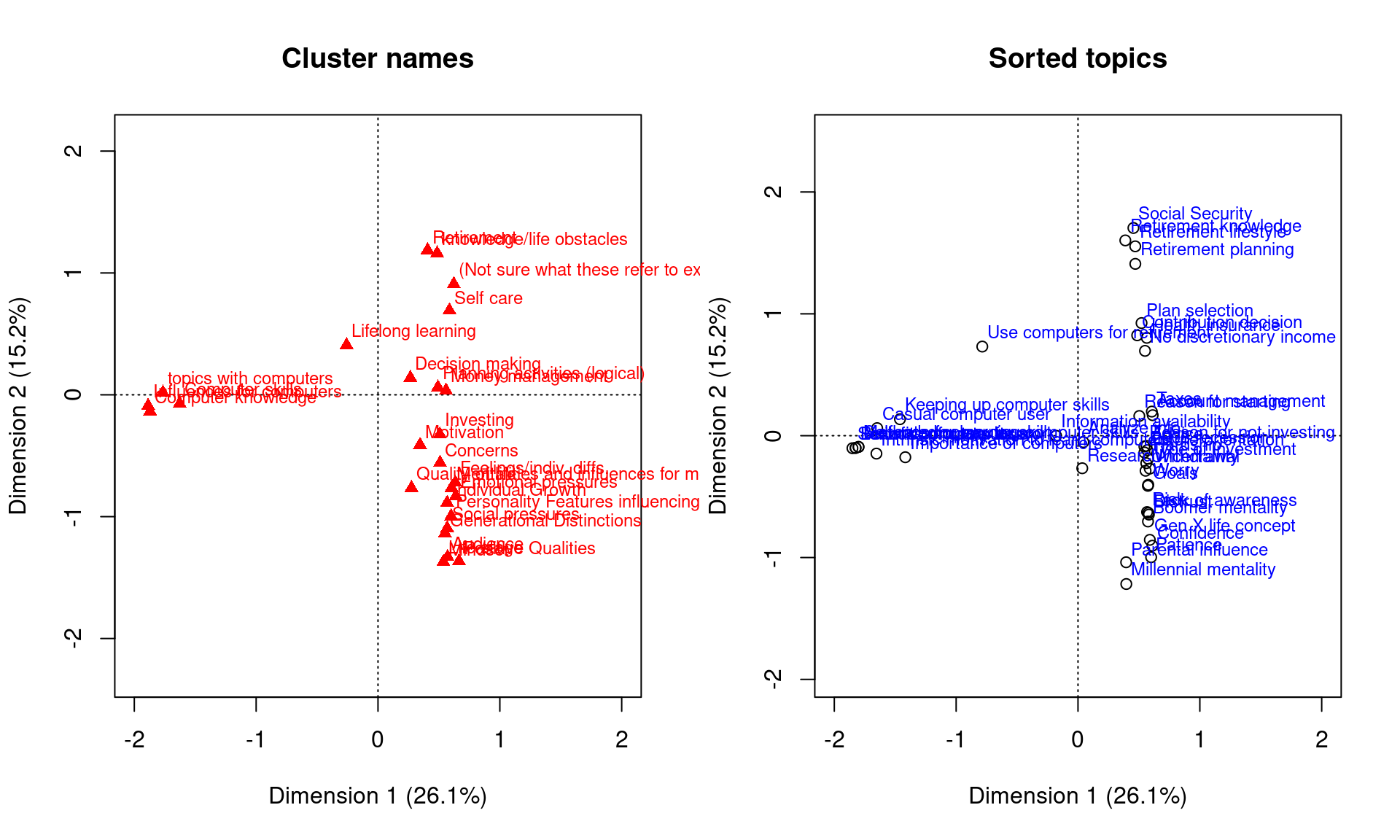
# points(ca$colcoord[,1], ca$colcoord[,2],col=km$cluster,pch=16)