Simple Swept Surfaces

Given two curves C1(u) and
C2(v), a swept surface is the surface
generated by moving curve C1(v) along curve
C2(u).
Curve C1(v) may be rotated and scaled.
More precisely, for each t in the domain of curve
C2(v), curve
C1(u) is moved to the point
C2(t), possibly with rotation and scaling.
Therefore, as t changes from 0 to 1, the transformed curve
C1(u) sweeps out a surface and hence the
name swept surface. Under this definition, curves
C1(u) and
C2(v) are referred to as the
profile curve and trajectory curve,
respectively.
Unfortunately, even though curves C1(u) and
C2(v) are both NURBS curves, the generated
swept surface may not have a NURBS representation. This will cause
problems, since the resulting surface cannot be processed with existing
techniques. As a result, this system only supports the generation of
swept surface without rotation and scaling. In other word,
curve C1(u) only slides along curve
C2(v) with the same orientation.
To design a swept surface, select
Advanced Features followed by
Cross Sectional Design. This will
bring up the curve system. In the curve system, one must do the following
to obtain a correct swept surface:
- Design a profile curve.
- Design a trajectory curve. Note that the profile and trajectory
curves do not have to be in the xz- and xy- planes.
- After adjusting the positions of these two curves,
in the curve system, use
Curve, followed by
Next Curve Segment
to make the profile curve the current curve segment.
- Select Techniques, followed by
Generate Swept Surface,
followed by
Using Identity Matrix.
The swept surface defined by these two curves will be shown
on the drawing canvas of the surface system.

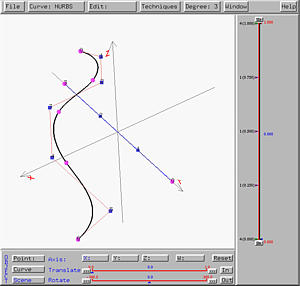
Example 1: A Swept Cylinder
The easiest swept surface is to have its trajectory curve a line segment.
In this case, the swept surface is simply a ruled surface. More precisely,
one can create a profile curve, translate it in the direction of the line
segment, and construct a ruled surface from these two identical copies of
profile curves (but in different locations). The resulting surface is the
same as a swept surface. In the following figure, the profile curve is the
one used to design a vase in the discussion of
surface revolution, and the trajectory
curve is a line segment on the x-axis.
Click here to download a
copy of this file swept-cy.dat.
After sending this design to the surface system, we shall see the following
swept surface. It is simply a cylinder generating from sliding the vase
curve along the line segment.
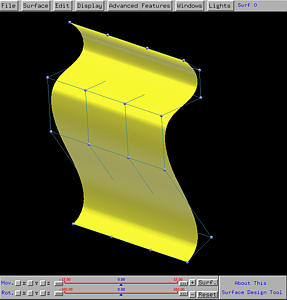
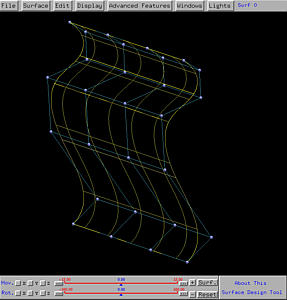

Example 2: A General Swept Surface
If the line segment is replaced with a NURBS curve, the resulting surface
will change, because the profile curve will follow the curvature of the
trajectory curve. The following example uses the same vase profile, but
changes the trajectory curve to a NURBS curve of degree 3.
Click here to download a
copy of this file swept-surf.dat.
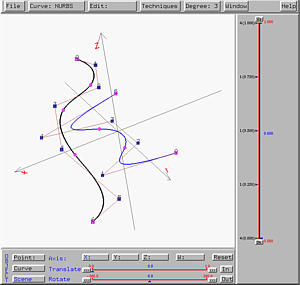
As you can see from the following figures, the vase profile follows the
curvature given by the trajectory.
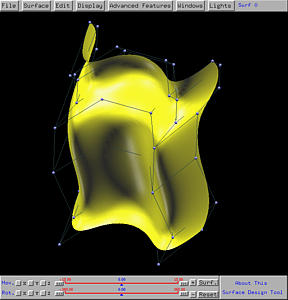
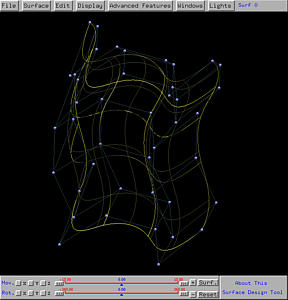

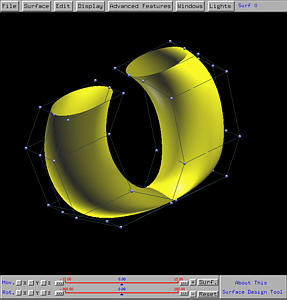
Example 3: A Swept Tube
With swept surfaces, a tube does not have to be linear like a cylinder or
circular like a torus. One can use a circle as a profile curve and
another curve as a trajectory curve. The following shows a circle
in the xz-plane as a trajectory and a NURBS of degree 3 not in the
xy-plane as the trajectory.
Click here to download a
copy of this file swept-tube.dat.
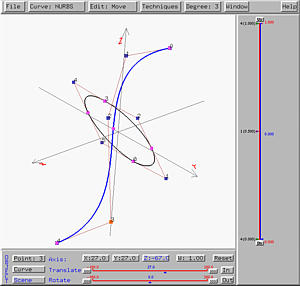
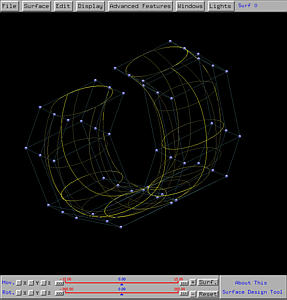
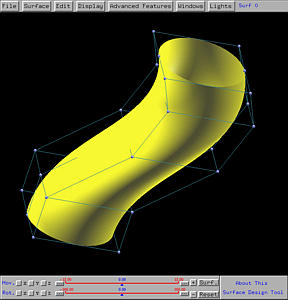
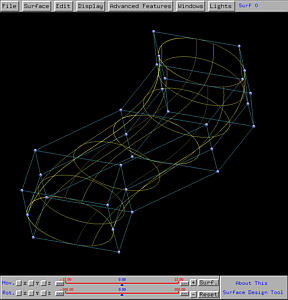
From the wireframe figure shown below, you will see that the tube is narrower
than the two ends. This is simply because the profile circle moves in
parallel with each other and as a result would stack together near the place
where the trajectory curve does not change shape "fast enough".

Example 4: A Bad Swept Surface Design
Let us continue with the previous example. We have a profile circle on the
xy-plane and a trajectory curve on the xz-plane. Click
here to download a copy of this file
swept-bad.dat.
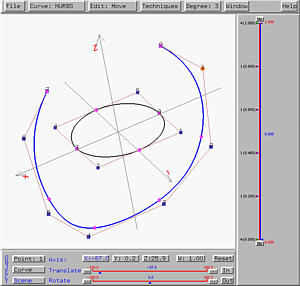
The following is the generated swept surface. As you can see from the
figure, the bottom part of the surface has a self-intersection. The
wireframe figures shows the cause of this self-intersection.