

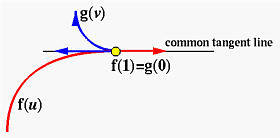
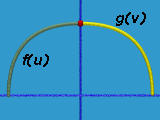
As mentioned in the discussion of B-rep, the edges and faces of a solid can be curve segments and surface patches rather than line segments and polygons. However, this may create some problems. In the figure shown below, we have three curvilinear patches of a B-rep joining together. Two boundary curve segments are shown in yellow and white meeting at a vertex X. Let these two curves be described as f(u) and g(v), where u and v are values in intervals [a,b] and [m,n], respectively. The problem is: how we can make sure that these curves join together in a "smooth" way.

Consider the "right-end" of curve f(b) and the "left-end" of curve g(m). If f(b) and g(m) are equal as shown in the above figure, we shall say curves f() and g() are C0 continuous at f(b)=g(m). If for all i <= k, the i-th derivatives at f(b) and g(m) are equal, we shall say that the curves are Ck continuous at point f(b)=g(m). Intuitively, two curves are C0 continuous at the joining point if we can go from one curve to the other without crossing a gap because these two curves connect to each other. Two curves are C1 continuous at the joining point if the speed (i.e., first derivative) does not change when crossing one curve to the other. Similarly, two curves are C2 continuous at the joining point if, in addition to the speed, the acceleration (i.e., second derivative) is also the same when crossing one curve to the other. Therefore, C1 continuous is "smoother" than C0 continuous at the joining point, C2 continuous is "smoother" than C1 continuous at the joining point, and so on. Moreover, if the curvatures of the curves at the joining point are equal, we will say they are curvature continuous at the joining point. Intuitively, two curves are curvature continuous if the turning rate is the same at the joining point; however, the second derivatives may not be the same at the joining point. In other words, curvature continuous does not guarantee C2 continuous; but, C2 continuous does imply curvature continuous. (Why?)
It is clear from the definition that if two curve segments are Ck continuous at f(b)=g(m), they are also Ci continuous for all i less than or equal to k. On the other hand, if the k-th derivatives of two curve segments at their joining point are not equal, they cannot be Ci continuous for any i larger than or equal to k.
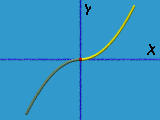
Let us take a look at a simple example. The following curve consists of two parabolas:
f(u) = ( u, -u2, 0 )where f(), the left curve, and g(), the right curve, have domains [-1,0] and [0,1], respectively. It is easy to check that f(0) = g(0) is the coordinate origin. Let us check to see if these two curves are C2 continuous there.
g(v) = ( v, v2, 0 )
The following are necessary information for this checking:
f'(u) = ( 1, -2u, 0 )Since f'(0) = g'(0) = ( 1, 0, 0 ), these two curves are C1 continuous at the origin. However, since f''(0) = ( 0, -2, 0 ) is not equal to g''(v) = ( 0, 2, 0 ), they are not C2 continuous at the origin. In fact, f''(u) points to the south while g''(u) points to north, and both are constant (i.e., do not change with u and v). Therefore, once a moving point crosses the origin from the green segment to the yellow segment, the second derivative changes its direction abruptly. Therefore, the curve segments are not C2 continuous at the origin.
f''(u) = ( 0, -2, 0 )
g'(u) = ( 1, 2v, 0 )
g''(v) = ( 0, 2, 0 )
Let us computes their curvatures:
Curvature of f(u) = 2/(1 + 4u2)1.5They have the same forms, although u is in [-1,0] and v is in [0,1]. Therefore, the two curve segments are curvature continuous at the joining point (i.e., f(0)= g(0))! Thus, we see that two curve segments may be C1 continuous and even curvature continuous, but not C2 continuous.
Curvature of g(v) = 2/(1 + 4v2)1.5

f(u) = A + u(B - A)where A, B and C are three collinear points as shown in the figure below.
g(v) = B + v(C - B)
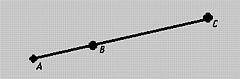
As u (resp., v) changes from 0 to 1, f(u) (resp., g(v)) runs from A to B (resp., B to C). Line segments f(u) and g(v) are obviously C0 continuous at the joining point B. Is it C1 continuous?
f'(u) = B - AThus, f'(u) = B - A is, in general, not equal to g'(v) = C - B and consequently these two line segments are not C1 continuous at the joining point B!
g'(v) = C - B
Is it strange? Yes, in fact, this is a problem of parameterization. If we replace the direction vectors B - A and C - B with unit-length vectors and change the domain of parameters u and v, this problem will disappear. That is, the above equations are changed to the following:
F(u) = A + u(B - A)/ | B - A |where u is in the range of 0 and | B - A | and v is in the range of 0 and | C - B |. Now, since we have F'(u) = G'(v) = the unit-length vector in the direction of A to C, the line segments are C1 continuous. Thus, reparameterizing the curve segments may overcome the problem.
G(v) = B + v(C - B)/ | C - B |
Let us look at another example, where PI is for 3.1415926 and u and v are in the range of [0,1].
f(u) = ( -cos(u2 PI/2), sin(u2 PI/2), 0 )
g(v) = ( sin(v2 PI/2), cos(v2 PI/2), 0 )
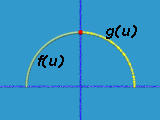
As u moves from 0 to 1, f(u) traces out the left part of the semi-circle. Similarly, as v moves from 0 to 1, g(u) traces out the right part of the semi-circle. These two have a joining point, shown in red, at (0,1,0) = f(1) = g(0). We have the following:
f'(u) = ( PI u sin(u2 PI/2), PI u cos(u2 PI/2), 0 )Note that both g'(0) and g''(0) are zero vectors and are not well-defined. As a result, we cannot talk about the continuity property at the joining point at all; but, from the figure, it "looks" like these two curves do have some continuity property because, at least, they have a common tangent line.
f''(u) = ( PI2 u2 cos(u2 PI/2), -PI2 u2 sin(u2 PI/2), 0 )
f'(u) × f''(u) = ( 0, 0, -PI3 u3 )
| f'(u) | = PI u
| f'(u) × f''(u) | = PI3 u3
k(u) = 1
g'(v) = ( PI v cos(v2 PI/2), -PI v sin(v2 PI/2), 0 )
g''(v) = ( -PI2 v2 cos(v2 PI/2), -PI2 v2 cos(v2 PI/2), 0 )
g'(v) × g''(v) = ( 0, 0, -PI3 u3 )
| g'(v) | = PI v
| g'(v) × g''(v) | = PI3 v3
k(v) = 1
Let us reparameterize these curves (i.e., change their parametric equations without changing their shapes). Let u2 = p in f(u) and let v2 = q in g(v). The new equations are:
f(p) = ( -cos(p PI/2), sin(p PI/2), 0 )Their derivatives are
g(q) = ( sin(q PI/2), cos(q PI/2), 0)
f'(p) = ( (PI/2) sin(p PI/2), (PI/2) cos(p PI/2), 0 )Therefore, after changing variables, both f'(1) and g'(0) are equal to ( PI/2, 0, 0 ) and hence they are C1 continuous. Moreover, both f''(1) and g''(0) are equal to ( 0, -(PI/2)2, 0 ) and hence they are C2 continuous! They are also curvature continuous because they have curvature 1 everywhere (remember they are circles). Thus, reparameterization or change of variables have a dramatic impact on continuity.
f''(p) = ( (PI/2)2 cos(p PI/2), -(PI/2)2 sin(p PI/2), 0 )
g'(q) = ( (PI/2) cos(q PI/2), -(PI/2) sin(q PI/2), 0 )
g''(q) = ( -(PI/2)2 sin(q PI/2), -(PI/2)2 cos(q PI/2), 0 )
f'(p) × f''(p) = g'(q) × g''(q) = ( 0, 0, -(PI/2)3 )
| f'(p) × f''(p) | = | g'(q) × g''(q) | = (PI/2)3
| f'(p) | = | g'(q) | = PI/2
k(p) = k(q) = 1

Let a curve segment have length s. One can parameterize this curve such that f(u) is the point having a distance u from the initial point f(0), where u is in the range of 0 and s. With this arc length parameterization, as u moves from 0 to s, f(u) moves on the curve from f(0) to f(s) in the same speed. Therefore, the tangent vector which measures speed is of unit-length. Not only this, many formulas shown on this and previous pages can be simplified.
Why don't we use arc length parameterization to simplify our computation? The answer is quite simple. While arc length parameterization is simple and elegant in theory, it is tedious in computation and impractical. One can easily design a curve in some handy parameterization; but, reparameterizing it with arc length sometime is extremely difficult. That is, finding arc length is not an easy task, since it requires to integrate a function involving the use of square root.
Therefore, even though non-arc length parameterization could cause problems, we will not use the arc length parameterization.

Two curve segments are said Gk geometric continuous at the joining point if and only if all i-th derivatives, i less than or equal to k, computed with arc length parameters agree at the joining point.Oops, we use arc length in the definition! But, don't worry, since arc length parameterization is not required as shown by the following equivalent definition:
Two curve segments are said Gk geometric continuous at the joining point if and only if there exists two parameterizations, one for each curve segment, such that all i-th derivatives, i less than or equal to k, computed with these new parameterizations agree at the joining point.This is better but not good enough because we really do not know how to find such parameterizations. Fortunately, the cases of k = 1 and k = 2 are very simple. Let us start with the case of k=1.
Two C0 curve segments are said G1 geometric continuous at the joining point if and only if vectors f'(u) and g'(v) are in the same direction at the joining point. Note that f'(u) and g'(v) are evaluated at the joining point.Since the tangent vectors at the joining point have the same direction, both curves have the same tangent line at the joining point. However, the converse does not hold. More precisely, two curve segments having the same tangent line does not imply they are G1 at the joining point. In the following figure, curves f(u) and g(v) have a common point at which the tangent lines are the same. However, the tangent vectors point to the opposite directions, and, as a result, they are not G1 at the joining point. Based on this definition, all previously discussed example curves are G1 at the joining points.
G. Neilson has found a very simple formula for G2 continuity as follows:
Two C1 curve segments are said G2 geometric continuous at the joining point if and only if vector f''(u) - g''(v) is parallel to the tangent vector at the joining point. Note that f''(u) and g''(v) are evaluated at the joining point.The beauty of this characterization for G2 continuity is that it works for any parameterization. Before using this characterization, you should check for C1 condition first.
Let us use an example to illustrate Nielson's result. Consider the following two parabola segments with joining point at ( 0, 1, 0):
f(u) = ( -1 + u2, 2u - u2, 0 )Both segments have domain [0, 1]. The joining point is f(1) = g(0) = ( 0, 1, 0 ).
g(v) = ( 2u - u2, 1 - u2, 0 )
The following are essential calculations:
f'(u) = ( 2u, 2 - 2u, 0 )From f'(1) = g'(0) = ( 2, 0, 0 ), we know that these two curve segments are C1 at the joining point. Since f''(1) = ( 2, -2, 0 ) is not equal to g''(0) = ( -2, -2, 0 ), they are not C2. But, since their curvature functions are the same (i.e., kf(u) = kg(v)=1), these two curves are curvature continuous at the joining point.
f''(u) = ( 2, -2, 0 )
f'(u) × f''(u) = ( 0, 0, -4 )
| f'(u) | = 2SQRT(1 - 2u + 2u2 )
| f'(u) × f''(u) | = 4
k(u) = 1/(2(1 - 2u + 2u2)1.5)
g'(v) = ( 2 - 2v, -2v, 0 )
g''(v) = ( -2, -2, 0 )
g'(v) × g''(v) = ( 0, 0, -4 )
| g'(v) | = 2SQRT(1 - 2v + 2v2 )
| g'(v) × g''(v) | = 4
k(v) = 1/(2(1 - 2v + 2v2)1.5)
Let us check for G2. Since the curves are C1, checking for G2 is meaningful. Since f''(1) - g''(0) = ( 4, 0, 0 ) is parallel to the tangent vector ( 2, 0, 0 ) at the joining point, these two curve segments are G2 continuous at the joining point ( 0, 1, 0 ).
By the definition of Gk, you could find two parameterizations, not necessarily of arc length type, so that the reparameterized segments are of C2.