Interior, Exterior and Closure

We need the concept of interior, exterior and closure to fully appreciate the discussion of regularized Boolean operators. Intuitively, the interior of a solid consists of all points lying inside of the solid; the closure consists of all interior points and all points on the solid's surface; and the exterior of a solid is the set of all points that do not belong to the closure.

Consider a sphere, x2 + y2 + z2 = 1. Its interior is the set of all points that satisfy x2 + y2 + z2 < 1, while its closure is x2 + y2 + z2 <= 1. Therefore, the closure is the union of the interior and the boundary (its surface x2 + y2 + z2 = 1). Obviously, its exterior is x2 + y2 + z2 > 1.

A solid is a three-dimensional object and so does its interior and exterior. However, its boundary is a two-dimensional surface.

Formal Definitions

Recall that the open ball with center (a,b,c) and radius r consists of all points that satisfy the following relation:
(x - a)2 + (y - b)2 + (z - c)2 < r2
A point P is an interior point of a solid S if there exists a radius r such that the open ball with center P and radius r is contained in the solid S. The set of all interior points of solid S is the interior of S, written as int(S). Based on this definition, the interior of an open ball is the open ball itself.

On the other hand, a point Q is an exterior point of a solid S if there exists a radius r such that the open ball with center Q and radius r does not intersect S. The set of all exterior point of solid S is the exterior of solid S, written as ext(S).

Those points that are not in the interior nor in the exterior of a solid S constitutes the boundary of solid S, written as b(S). Therefore, the union of interior, exterior and boundary of a solid is the whole space.

The closure of a solid S is defined to be the union of S's interior and boundary, written as closure(S). Or, equivalently, the closure of solid S contains all points that are not in the exterior of S.

Examples

Here is an example in the plane. You should change all open balls to open disks. Point A is an interior point of the shaded area since one can find an open disk that is contained in the shaded area. Similarly, point B is an exterior point. Point C is a boundary point because whatever the radius the corresponding open ball will contain some interior points and some exterior points.

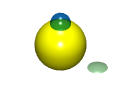
Note that a surface (a two-dimensional object) is never a solid (a three-dimensional object). In fact, a surface does not have any interior point. Take any point of the surface (see figure below), the open ball with arbitrary radius and center at that point always intersects the sphere in an open disk (in pale green in the lower right corner). Therefore, no open ball can be contained in the sphere, and, as a result, that point is not an interior point of the sphere. Thus, we conclude that a surface does not have any interior point.