B-spline Basis Functions: Definition

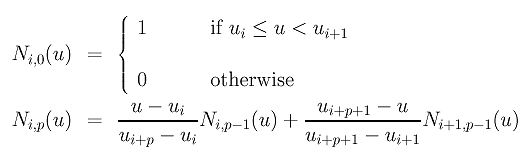
Bézier basis functions are used as weights. B-spline basis functions will be used the same way; however, they are much more complex. There are two interesting properties that are not part of the Bézier basis functions, namely: (1) the domain is subdivided by knots, and (2) basis functions are not non-zero on the entire interval. In fact, each B-spline basis function is non-zero on a few adjacent subintervals and, as a result, B-spline basis functions are quite "local".

Let U be a set of m + 1 non-decreasing numbers, u₀ <= u₂ <= u₃ <= ... <= u_m. The u_i's are called knots, the set U the knot vector, and the half-open interval [u_i, u_i+1) the i-th knot span. Note that since some u_i's may be equal, some knot spans may not exist. If a knot u_i appears k times (i.e., u_i = u_i+1 = ... = u_i+k-1), where k > 1, u_i is a multiple knot of multiplicity k, written as u_i(k). Otherwise, if u_i appears only once, it is a simple knot. If the knots are equally spaced (i.e., u_i+1 - u_i is a constant for 0 <= i <= m - 1), the knot vector or the knot sequence is said uniform; otherwise, it is non-uniform.

The knots can be considered as division points that subdivide the interval [u₀, u_m] into knot spans. All B-spline basis functions are supposed to have their domain on [u₀, u_m]. In this note, we use u₀ = 0 and u_m = 1 frequently so that the domain is the closed interval [0,1].

To define B-spline basis functions, we need one more parameter, the degree of these basis functions, p. The i-th B-spline basis function of degree p, written as N_i,p(u), is defined recursively as follows:

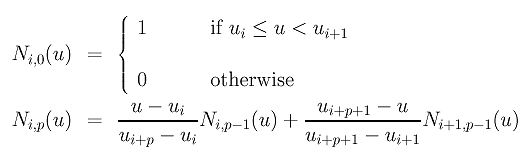
The above is usually referred to as the Cox-de Boor recursion formula. This definition looks complicated; but, it is not difficult to understand. If the degree is zero (i.e., p = 0), these basis functions are all step functions and this is what the first expression says. That is, basis function N_i,0(u) is 1 if u is in the i-th knot span [u_i, u_i+1). For example, if we have four knots u₀ = 0, u₁ = 1, u₂ = 2 and u₃ = 3, knot spans 0, 1 and 2 are [0,1), [1,2), [2,3) and the basis functions of degree 0 are N_0,0(u) = 1 on [0,1) and 0 elsewhere, N_1,0(u) = 1 on [1,2) and 0 elsewhere, and N_2,0(u) = 1 on [2,3) and 0 elsewhere. This is shown below:

To understand the way of computing N_i,p(u) for p greater than 0, we use the triangular computation scheme. All knot spans are listed on the left (first) column and all degree zero basis functions on the second. This is shown in the following diagram.

To compute N_i,1(u), N_i,0(u) and N_i+1,0(u) are required. Therefore, we can compute N_0,1(u), N_1,1(u), N_2,1(u), N_3,1(u) and so on. All of these N_i,1(u)'s are written on the third column. Once all N_i,1(u)'s have been computed, we can compute N_i,2(u)'s and put them on the fourth column. This process continues until all required N_i,p(u)'s are computed.

In the above, we have obtained N_0,0(u), N_1,0(u) andN_2,0(u) for the knot vector U = { 0, 1, 2, 3 }. Let us compute N_0,1(u) and N_1,1(u). To compute N_0,1(u), since i = 0 and p = 1, from the definition we have

Since u₀ = 0, u₁ = 1 and u₂ = 2, the above becomes

Since N_0,0(u) is non-zero on [0,1) and N_1,0(u) is non-zero on [1,2), if u is in [0,1) (resp., [1,2) ), only N_0,0(u) (resp., N_1,0(u) ) contributes to N_0,1(u). Therefore, if u is in [0,1), N_0,1(u) is uN_0,0(u) = u, and if u is in [1,2), N_0,1(u) is (2 - u)N_1,0(u) = (2 - u). Similar computation gives N_1,1(u) = u - 1 if u is in [1,2), and N_1,1(u) = 3 - u if u is in [2,3). In the following figure, the black and red lines are N_0,1(u) and N_1,1(u), respectively. Note that N_0,1(u) (resp., N_1,1(u)) is non-zero on [0,1) and [1,2) (resp., [1,2) and [2,3)).

Once N_0,1(u) and N_1,1(u) are available, we can compute N_0,2(u). The definition gives us the following:

Plugging in the values of the knots yields

Note that N_0,1(u) is non-zero on [0,1) and [1,2) and N_1,1(u) is non-zero on [1,2) and [2,3). Therefore, we have three cases to consider:

1. u is in [0,1):
   In this case, only N_0,1(u) contributes to the value of N_0,2(u). Since N_0,1(u) is u, we have
   

2. u is in [1,2):
   In this case, both N_0,1(u) and N_1,1(u) contribute to N_0,2(u). Since N_0,1(u) = 2 - u and N_1,1(u) = u - 1 on [1,2), we have
   

3. u is in [2,3):
   In this case, only N_1,1(u) contributes to N_0,2(u). Since N_1,1(u) = 3 - u on [2,3), we have
   

Two Important Observations

Since N_i,1(u) is computed from N_i,0(u) and N_i+1,0(u) and since N_i,0(u) and N_i+1,0(u) are non-zero on span [u_i, u_i+1) and [u_i+1, u_i+2), respectively, N_i,1(u) is non-zero on these two spans. In other words, N_i,1(u) is non-zero on [u_i, u_i+2). Similarly, since N_i,2(u) depends on N_i,1(u) and N_i+1,1(u) and since these two basis functions are non-zero on [u_i, u_i+2) and [u_i+1, u_i+3), respectively, N_i,2(u) is non-zero on [u_i, u_i+3). In general, to determine the non-zero domain of a basis function N_i,p(u), one can trace back using the triangular computation scheme until it reaches the first column. The covered spans are the non-zero domain of this basis function. For example, suppose we want to find out the non-zero domain of N_1,3(u). Based on the above discussion, we can trace back in the north-west and south-west directions until the first column is reached as shown with the blue dotted line in the following diagram. Thus, N_1,3(u) is non-zero on [u₁, u₂), [u₂, u₃), [u₃, u₄) and [u₄, u₅). Or, equivalently, it is non-zero on [u₁, u₅).

In summary, we have the following observation:

Basis function N_i,p(u) is non-zero on [u_i, u_i+p+1). Or, equivalently, N_i,p(u) is non-zero on p+1 knot spans [u_i, u_i+1), [u_i+1, u_i+2), ..., [u_i+p, u_i+p+1).

Next, we shall look at the opposite direction. Given a knot span [u_i, u_i+1), we want to know which basis functions will use this span in its computation. We can start with this knot span and draw a north-east bound arrow and a south-east bound arrow. All basis functions enclosed in this wedge shape use N_i,0(u) (why?) and hence are non-zero on this span. Therefore, all degree p basis functions that are non-zero on [u_i, u_i+1) are the intersection of this wedge and the column that contains all N_i,p(u)'s. In fact, this column and the two arrows form an equilateral triangle with this column being the vertical side. Counting from N_i,0(u) to N_i,p(u) there are p+1 columns. Therefore, the vertical side of the equilateral triangle must have at most p+1 entries, namely N_i,p(u), N_i-1,p(u), N_i-2,p(u), ..., N_i-p+2,p(u), N_i-p+1,p(u) and N_i-p,p(u).

Let us take a look at the above diagram. To find all degree 3 basis functions that are non-zero on [u₄, u₅), draw two arrows and all functions on the vertical edges are what we want. In this case, they are N_1,3(u), N_2,3(u), N_3,3(u), and N_4,3(u). This is shown with the orange triangle. The blue (resp., red) triangle shows the degree 3 basis functions that are non-zero on [u₃, u₄) (resp., [u₂, u₃) ). Note that there are only three degree three basis polynomials that are non-zero on [u₂, u₃).

In summary, we have observed the following property.

On any knot span [u_i, u_i+1), at most p+1 degree p basis functions are non-zero, namely: N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., N_i-1,p(u) and N_i,p(u),

What Is the Meaning of the Coefficients?