B-spline Curves: Closed Curves

There are many ways to generate closed curves. The simple ones are
either wrapping control points or wrapping knot vectors.

Wrapping Control Points
Suppose we want to construct a closed B-spline curve
C(u) of degree p
defined by n+1 control points P0,
P1, ..., Pn. The number of
knots is m+1, where m = n + p + 1.
Here is the construction procedure:
- Design an uniform knot sequence of m+1 knots:
u0 = 0, u1 = 1/m,
u1 = 2/m, ...,
um = 1. Note that the domain of the curve
is [up, un-p].
See the discussion in
open curves for the details.
- Wrap the first p and last p control points.
More precisely, let
P0 = Pn-p+1,
P1 = Pn-p+2, ...,
Pp-2
= Pn-1 and
Pp-1
= Pn. This is shown in the figure
below.
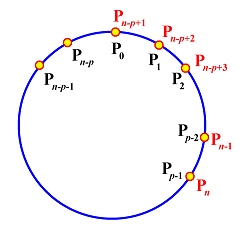
The constructed curve is Cp-1 continuous
at the joining point C(up) =
C(un-p).
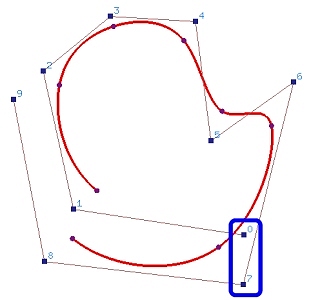
The following is an example. Figure (a) shows an open B-spline curve of
degree 3 defined by 10 (n = 9) control points and a uniform knot
vector. In the figure, control point pairs 0 and 7, 1 and 8, and 2 and 9
are placed close to each other to illustrate the construction.
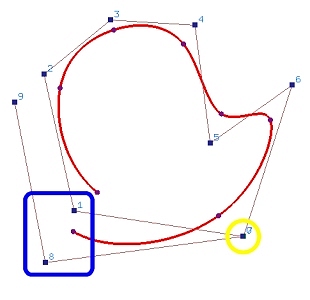
Figure (b) shows the result of making control points 0 and 7 identical.
The shape of the curve does not change very much. Then, control points 1 and
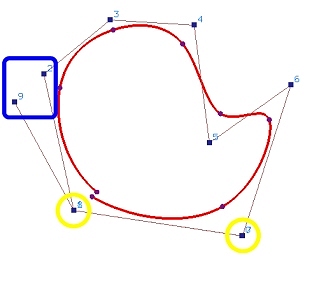
8 are made identical as shown in Figure (c). It is clear that the gap
between the first and last points of the curve is closer. Finally, the curve
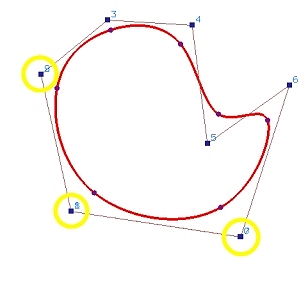
becomes a closed on when control points 2 and 9 are made identical as
shown in Figure (d).

Wrapping Knots
Another way of constructing closed B-spline curves is by wrapping knots.
Suppose we want to construct a closed B-spline curve
C(u) of degree p defined by n+1 control points
P0, P1, ..., Pn.
The following is the construction procedure:
- Add a new control point Pn+1 =
P0. Therefore, the number of control points
is n+2.
- Find an appropriate knot sequence of n+1 knots
u0, u1, ...,
un. These knots are not necessarily
uniform, an advantage over the method discussed above.
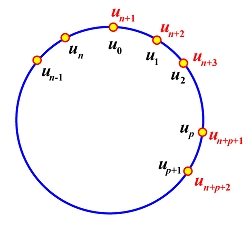
- Add p+2 knots and wrap around the first p+2 knots:
un+1 = u0,
un+2 = u1,
...,
un+p = up-1,
un+p+1 =
up,
un+p+2 =
up+1 as shown in the following
diagram. In this way, we have n+p+2 =
(n+1) + p + 1 knots.
- The open B-spline curve C(u) of degree p
defined on the above constructed n+1 control points
and n+p+2 knots is a closed curve with
Cp-1 continuity at the joining point
C(u0)
= C(un+1).
Note that the domain of this closed curve is
[u0, un+1].