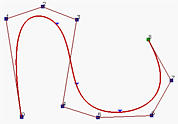
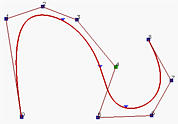
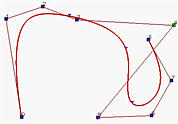

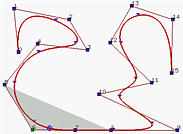
Moving control points is the most obvious way of changing the shape of a B-spline curve. The local modification scheme discussed on an earlier page states that changing the position of control point Pi only affects the curve C(u) on interval [ui, ui+p+1), where p is the degree of a B-spline curve. In fact, the shape change is translational in the direction of the control point being moved. More precisely, if control point Pi is moved in certain direction to a new position Qi, then point C(u), where u is in [ui, ui+p+1), will be moved in the same direction from Pi to Qi. However, the distance moved is different from point to point. In the following figures, control point P4 is moved from the position in the left figure to a new position in the middle figure and finally to its final position in the right figure. As you can see those points corresponding to knots (marked with little triangles) are moved in the same direction.



Let us take a look at some details. Suppose C(u) is a given B-spline curve of degree p defined as follows:
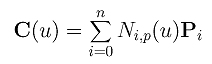
Let control point Pi be moved to a new position Pi + v. Then, the new B-spline curve D(u) of degree p is the following:
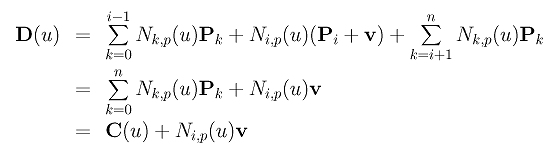
Therefore, the new curve D(u) is simply the sum of the original curve C(u) and a translation vector Ni,p(u)v. Since Ni,p(u) is non-zero on the interval [ui,ui+p+1), if u is not in this interval, this "translation" term is zero. Hence, moving a control point only affects the shape of a section of the given curve. The left curve below is a B-spline curve of degree 4 (i.e., p = 4) defined by 13 control points (i.e., n = 12) and 18 knots (i.e., m = 17). These 18 knots are all simple and define a clamped curve (i.e., u0 = u1 = u2 = u3 = u4 = 0 and u13 = u14 = u15 = u16 = u17 = 1). The remaining knots define 9 knot spans and hence 9 curve segments as shown in the figure. These nine knot spans and curve segments are named as follows:
| Span | [u4,u5) | [u5,u6) | [u6,u7) | [u7,u8) | [u8,u9) | [u9,u10) | [u10,u11) | [u11,u12) | [u12,u13) |
| Segment | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
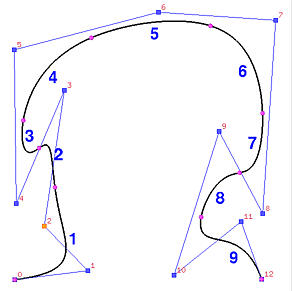
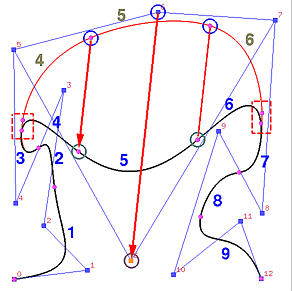
Now let us move P6. The result is shown in the right figure above. As you can see, the curve is moved in the same direction. The coefficient of P6 is N6,4(u), which is non-zero on [u6, u11). Thus, moving P6 affects curve segments 3, 4, 5, 6 and 7. Curve segments 1, 2, 8 and 9 are not affected.

If u lies in knot span [ui,ui+1), then C(u) lies in the convex hull defined by p+1 control points Pi, Pi-1, ..., Pi-p+1, Pi-p. Since this is true for all u in that span, the curve segment on this knot span lies entirely in this convex hull. If all of these p+1 control points are collinear (i.e., on a straight line), the convex hull collapses to a line segment and so does the curve segment it contains. As a result, the curve segment on knot span [ui,ui+1) becomes a line segment. Note that in this case only this curve segment becomes a line segment. Other curve segments are still non-linear.
|
|
|
| (a) | (b) | (c) |
|
|
|
| (d) | (e) | (f) |
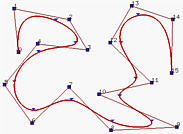
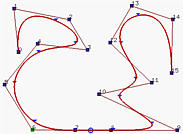
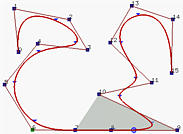
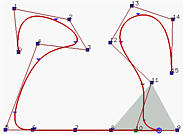
Let us take a look at an example. Figures above are defined by n = 15 (i.e., 16 control points), p = 3 (degree 3) and m = 19 (i.e., 20 knots). Note that the first four and last four knots are clamped. Figure (a) is the given B-spline curve. Let us make P9, P8, P7 and P6 collinear. Therefore, the curve segment on [u9,u10) lies in the convex hull defined by P9, P8, P7 and P6. Since this convex hull is a line segment, the curve segment must also be a line segment. Keep in mind that the first four knots are clamped and hence the first three knot spans do not exist. Since [u9,u10) is the seventh knot span, the seventh segment collapses to the line segment P7P8. This is illustrated by figures (b), (c) and (d).
But, why is the curve segment on [u9,u10) the only collapsed curve segment? Look at Figure (b). The shaded area is the convex hull just before u enters [u9,u10). This convex hull is defined by control points P8, P7, P6 and P5, which is still not a line segment yet. Once u enters [u9,u10), the curve segment collapses (Figure (c)). Immediately after u leaving [u9,u10), a new convex hull appears (Figure (d)).
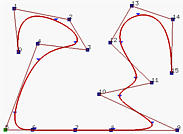
Figure (e) has P5 collinear with its four successors. The curve contains one more line segment. Figure (f) has P10 collinear with its five predecessors; however, it is moved to a position between P8 and P9. This would make part of the corresponding curve segment a straight line (why?)
Consider control Pi. Since the curve segment on knot span [ui, ui+1) lies entirely in the convex hull defined by Pi, ..., Pi-p+1,Pi-p, if we make the first p control point identical (i.e., Pi = Pi-1 = ... = Pi-p+1), the convex hull collapses to a line segment Pi-pPi and the curve must pass Pi.
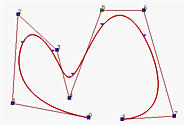

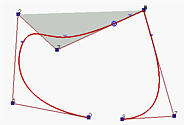
The curve in the left figure above is of degree 3. If P5 is moved and made identical with P6, the curve is moved closer to P6 but not passing though it yet. This is shown in the middle figure. Note that the number of curve segments is not changed due to this move; however, the little triangle marker near to P5 is move closer to P6. If P4 is moved and made identical to P6 = P5, the curve passes through P6 and the point that corresponds to a knot becomes identical to control point P4 due to this move.
In the above, p adjacent control points are made identical. At that control point, the continuity is C0 because the curve has a cusp (see the right figure above). However, a B-spline curve is Cp-1 at simple knots and infinitely differentiable at other places, the curve is Cp-1 continuous at control point Pi (the collapsed control point renumbered to i) on leg Pi-pPi and is also Cp-1 continuous at control point Pi on leg PiPi+1. Therefore, if we make control points Pi-p, Pi and Pi+1 collinear, as long as the two adjacent curve segments do not have a cusp at the knot, they are Cp-1 continuous at Pi.

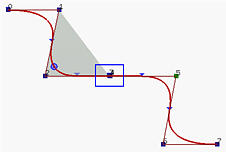
In the above figure figures, the curve is of degree 2. If we make control points 2, 3, 4 and 5 collinear and 3 and 4 identical, we have the right figure. The collinearity makes sure the curve segment lies on the line while the identical control points enforce the C3-1 = C2 continuous.