Why Is the Degree Elevation Algorithm Correct?

We shall establish the correctness of the degree elevation algorithm. Again, it requires simple, but tedious, calculations. Suppose the given Bézier curve C(u) of degree n is defined by control points P₀, P₁ , ..., P_n, and the degree elevated Bézier curve D(u) of degree n+1 is defined by control points Q₀ = P₀, Q₁, Q₂, ..., Q_n, Q_n+1 = P_n. We shall find the n unknown control points Q_i's.

Our strategy is very simple. Since C(u) and D(u) are the same curve, their derivatives at any u should be equal. Hence, by comparing the first, second, third, ..., and n-th derivatives at 0, we should be able to determine what Q_i's are. To simplify our calculation, we shall use mathematical indiction. More precisely, we find Q₁ by comparing the first derivatives at 0. Then, we assume that Q₁, Q₂, ..., Q_k-1 are computed and use these known results to compute Q_k. Iterating this process n times, we will compute all new control points.

The Base Case

The first derivative of C(u) is

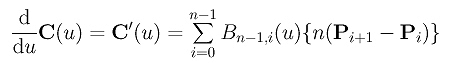
Thus, the derivative at u = 0 is n(P₁ - P₀). Similarly, the derivative of D(u) at u = 0 is (n+1)(Q₁-Q₀) = (n+1)(Q₁-P₀). Because these two derivatives are equal, we have

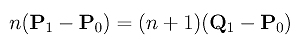
Solving for Q₁, we have our first result:

The Induction Step

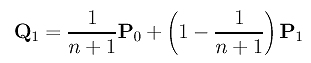
For the induction step, we shall assume that the computation of Q₀ = P₀, Q₁, ..., Q_k-1 are correct and show that Q_k is also correct. This is done by comparing the k-th derivatives of the original curve C(u) and the degree elevated curve D(u).

Just like in the base case, we actually do not need the complete curves. Let the k-th derivative of C(u) and D(u) be C^[k](u) and D^[k](u), respectively. The k-th derivative vectors at u = 0 are C^[k](0) and D^[k](0). Because C(u) and D(u) are the same curve, their k-th derivatives at u = 0 should be identical. More precisely, we should have C^[k](0) = D^[k](0). From this relation and the known Q₀ = P₀, Q₁, ..., Q_k-1, we shall compute Q_k.

In the discussion of higher derivatives, we know that the k-th derivative function of curve C(u) is

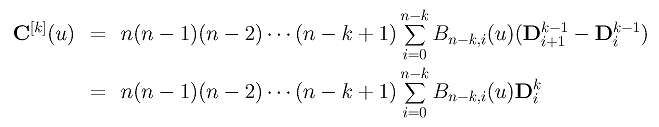
where D^k_i is

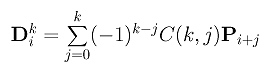
and the combinatorial coefficient C(k,j) is

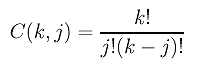
The computation of the D^k_i's is an exercise at the end of this unit. Click here if you wish to see the details. Therefore, C^[k](0) is computed as follows:

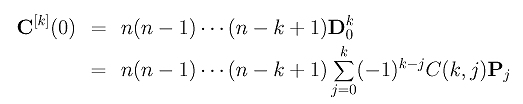
Similarly, we can compute D^[k](0). Note that curve D(u) is of degree n+1. This is the reason that the multiplier is (n+1)n(n-1)...(n-k+2).

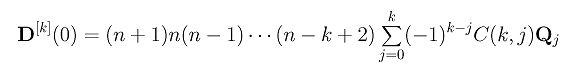
Setting C^[k](0) equal to D^[k](0) and canceling some common factors yields the following:

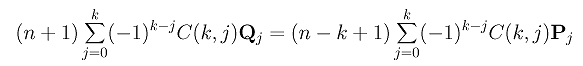
In fact, we can do more. Since we know (1) Q_k is unknown and Q₀ = P₀, we can take these two terms out of the summation of D^[k](0). Now, the summation runs from 1 to k-1. To make the summation in C^[k](0) compatible, we also take the terms of P_k and P₀ out of the summation. This gives the following:

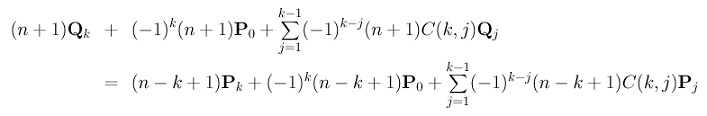
Rearranging the terms yields the following:

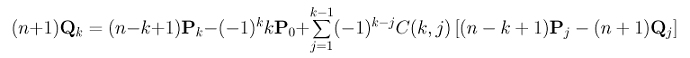
By the induction hypothesis, for j in the range of 0 and k-1, Q_j is known and is computed as follows:

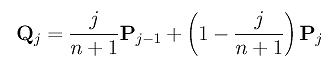
Plug Q_j into the term in the summation and we have:

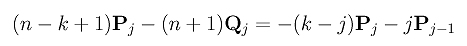
Plug this result back into the expression of (n+1)Q_k and split the summation into two:

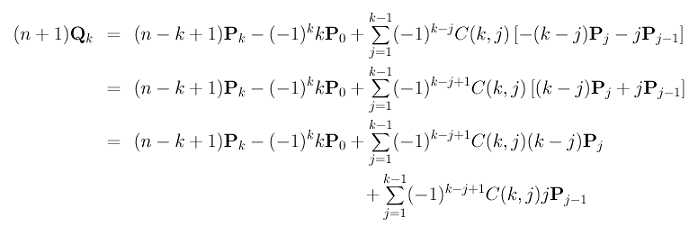
After taking P_k-1 out of the first summation, the first summation becomes:

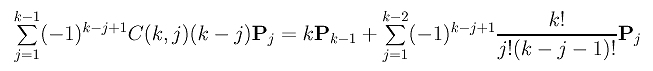
Then, we take the P₀ term out of the second summation:

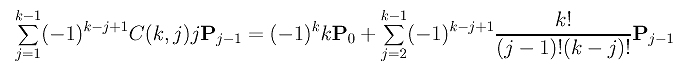
However, in this expression, the index j runs from 2 to k-1. To make it compatible with that of the first summation, we can use a new index h = j - 1. After this substitution, the second summation becomes the following:

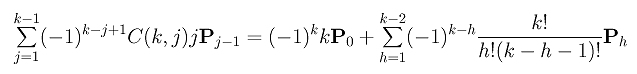
Note that the corresponding terms in these two summations are equal with different signs (i.e., (-1)^k-j+1=(-1)×(-1)^k-j in the first summation and (-1)^k-h in the second). Hence, adding these two summations together will cancel out all terms in the summation and yield the following:

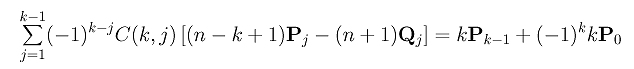
Putting this back into the expression of (n+1)Q_k yields

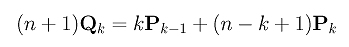
Dividing the expression by n+1 gives us the desired result:

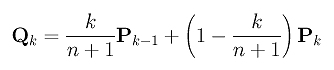
Therefore, the degree elevation computation for k also holds, and the degree elevation algorithm is correct.