Problems

1. Given three control points on the xy-plane (-1,0), (0,1) and (2,0), do the following:
   • Write down its Bézier curve equation.
   • Expand this equation to its equivalent conventional form.
   • Since there are three control points, there are three Bézier coefficients. Write down their equations and sketch their graphs.
   • Use your calculator to find enough number of points using the conventional parametric form and sketch the curve.
   • Find points on the curve that correspond to u = 0, 0.25, 0.5, 0.75 and 1 with the conventional form.
   • Use de Casteljau's algorithm to find points on the curve corresponding to u = 0, 0.25, 0.5, 0.75 and 1.
   • Subdivide the Bézier curve at u = 0.4 and list the control points of the resulting curve segments.
   • Increase the degree of this curve to three and list the new set of control points. Then, increase the degree to four and list the new set of control points.
2. In the variation diminishing property, what if you have a line or a plane that passes through a control point or contains a line segment of the control polyline? Suggest a proper counting of intersection points and verify your claim with examples.
3. A Bézier curve of degree 2 defined by three control points P₀, P₁ and P₂ is a portion of a conic section. What type of this conic section is it? Is it a portion of a parabola, a hyperbola or an ellipse? You can assume the given control points are in the xy-coordinate plane.
4. Suppose Bézier curve C(u) (resp., D(u)) of degree n is defined by control points P₀, P₁, ..., P_n (resp., O₀, Q₁, ..., Q_n). If the curves are identical (i.e., C(u) = D(u) for every u in [0,1]), then the corresponding control points are also identical (i.e., P_i = Q_i for all 0 <= i <= n).
   Hint: First show that if (1-u)A+uB is a zero vector for every u in [0,1], then A and B are both zero vectors. Then, work the de Casteljau's algorithm backward to show that P_i - Q_i is a zero vector for all 0 <= i <= n.
5. Suppose Bézier curve C(u) of degree n is defined by control points P₀, P₁, ..., P_n.
   1. Prove the following:
      

   2. Show that curve C(u) can be rewritten to the following matrix form:
      

      where entry m_ij is defined as follows:

      

   Therefore, a Bézier curve can be rewritten using the traditional polynomial form in u⁰ = 1, u¹, u², ...., uⁿ. This is the so-called monomial form and the basis functions are u⁰ = 1, u¹, u², ...., uⁿ. However, the use of this monomial form is computationally unstable.
6. Show that the maximum of B_n,i(u) occurs at u = i/n and that the maximum value is
   

7. Verify the following results with your calculus knowledge:
   • the derivative of B_n,i(u):
     

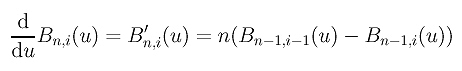
   • the derivative of Bézier curve p(u):
     

8. The discussion of joining two Bézier curves with C¹-continuity assumes the domain of the curves is [0,1]. Suppose the domain of the first curve is [0,s] and the domain of the second curve is [s,1]. Redo the calculation. What is your conclusion? Is there any modification required?
9. Prove the following:
   

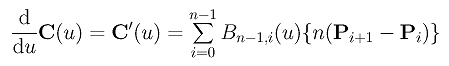
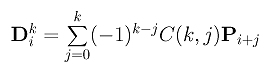
   where D_i^k's are the k-th difference points and C(k,j) is the binomial coefficient defined as follows:

   

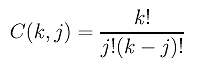
   With this formula, we can express a higher derivative using the original control points rather than using finite difference points.

10. After subdividing a Bézier curve of degree p at s, we have two Bézier curves of degree p, one on interval [0,s] while the other on [s,1]. Show that these two curves are of C¹ continuous at the joining point.
    Hint: Suppose the last two control points of the curve on [0,s] are P_p-1 and P_p, and the first two control points of the curve on [s,1] are Q₀ and Q₁. Then, we have P_p-1, P_p = Q₀ and Q₁ are on the same line, and the ratio of the distance from P_p-1 to P_p = Q₀ and the distance from P_p = Q₀ to Q₁ is equal to s due to subdivision. Now, change the variables of both curves so that they have domain on [0,1]. A simple calculation will lead to the desired conclusion.