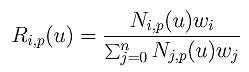

Since NURBS curves are defined by a set of control points, a knot vector, a degree and a set of weights, we have one more parameter for shape modification (i.e., the weights). Recall that the basis functions of a NURBS curve is
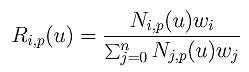
Therefore, increasing and decreasing the value of wi will increase and decrease the value of Ri,p(u), respectively. More precisely, increasing the value of wi will pull the curve toward control point Pi. In fact, all affected points on the curve will also be pulled in the direction to Pi. When wi approaches infinity, the curve will pass through control point Pi. On the other hand, decreasing the value of wi will push the curve away from control point Pi. Click here for an in-depth discussion.
The following figures show a NURBS curve of degree 6 and its NURBS basis functions. The selected control point is P9. In the first figure, all weights are 1's and the curve is a B-spline curve. In the second one, w9 is increased to 2 and, as you can see, a portion of the curve moves toward P9. Since w9 is increased, so does R9,6(u) as shown in the right figure.




In the following, w9 is further increased to 5, 10 and 20, the corresponding R9,6(u) becomes larger, and carries more weight. This pulls the curve further to control point P9. When w9 = 20, the curve is very close to P9.






Let us take a look at the opposite effect. The following is the initial case where all weights are 1's. Then, w9 is decreased to 0.5 and this pushes the curve away from control point P9. Note that the corresponding R9,6(u) decreases and so does the impact of control point P9 on the curve C(u). When w9 changes to 0.1, the curve is moved further away and the value of R9,6(u) is smaller. The last figure shows the curve of w9 being zero. Since R9,6(u) is zero, it has no impact on the curve and, as a result, the curve segment opposite to control point P9 is almost flat.








In summary, we have the following:
Increasing (resp., decreasing) the value of weight wi pulls (resp., pushes) the curve toward (resp., away from) control point Pi. When the value of wi becomes infinity, the curve passes through control point Pi and when wi is zero, control point Pi has no impact on the curve.

Let us be more precise about the impact of changing the weight of a selected control point. To this end, let us return to the definition of NURBS curves:
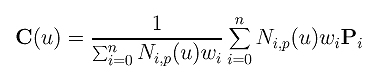
Let us select control point Pk and investigate the impact of changing wk. Since Pk can only contribute to the curve C(u) on the non-zero domain of its coefficient Nk,p(u) (i.e., [uk, uk+p+1)), in what follows, we assume u is in [uk, uk+p+1).
Taking the terms involving wk out of the summations yields the following:

Because this equation is quite complex, we shall simplify it with the following:

Then, the equation becomes the following easy-to-read one:

Consider the case of wk = 0 first. We have A = 0 and the point on curve, denoted as C0(u), is

Now let us calculate the vector from this "base" point C0(u) to its corresponding point C(u) for an arbitrary wk. Some simple manipulations yield the following:

What does this mean? It means vector C(u)-C0(u) and vector Ck-C0(u) have the same direction, and the length of the former is A/(A+B) times that of the latter for every u in [uk, uk+p+1)! Because points Ck and C0(u) are fixed, we can say that C(u) lies on the line of Pk and C0(u). Moreover, if all weights are non-negative, A and B are both non-negative and the value of A/(A+B) lies between 0 and 1! That is, point C(u) lies on the line segment of Pk and C0(u).
What if wk approaches infinity? Let us divide the numerator and denominator of the curve C(u) by wk as shown below.

If wk approaches infinity, 1/wk approaches zero. Hence, if wk approaches infinity, P(u) approaches Pk, the selected control point. The following summarizes what we have so far:
| If wk is non-negative, C(u) always lies on the line segment of C0(u) and Pk, where C0(u) is the point corresponding to wk = 0, and u is in [uk, uk+p+1). Moreover, when wk changes from 0 to infinity, C(u) moves from C0(u) to Pk, and if wk is infinity, C(u) becomes Ck. |
The following figure illustrates this result. We have a NURBS curve of degree 6 defined by 9 control points (n = 8) and 16 knots (m = 15) as shown below.
| u0 = u1 = u2 = u3 = u4 = u5 = u6 | u7 | u8 | u9 = u10 = u11 = u12 = u13 = u14 = u15 |
| 0 | 1/3 | 2/3 | 1 |
The selected control point is P4. Since the coefficient of P4, N4,6(u), is non-zero on [u4, u4+6+1) = [0,1), changing w4 affects the entire curve!

The points that correspond to u = 1/3 and u = 2/3 are marked on the curve in different colors. The curve corresponding to w4 = 0 is the lowest one marked with a 0. The figure shows the curves of w4 being 2, 3, 4, 5, 10, 20 and 50. As the value of w4 increases, the curve is pulled toward control point P4. When w4 is increased to 50, the curve becomes very close to P4. Note that all points that correspond to C(1/3) are on the line segment C0(1/3) and P4, and all points that correspond to C(2/3) are on line segment C0(2/3) and P4. Note also that the curve segment between C(1/3) and C(2/3) gets shorter as the value of w4 increases. Eventually, the length of this curve segment becomes zero (i.e., C(1/3) and C(2/3) become identical to P4) when w4 is infinity. Can you generalize this finding?