
Finally, we will be able to represent circular arcs and full circles. The former use rational Bézier curves and the latter use NURBS.
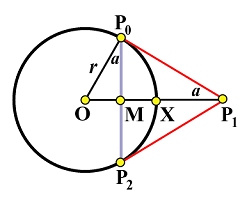
Since circles are special cases of ellipses, they can certainly be represented with rational Bézier curves of degree 2 with the only weight being < 1. Hence, if we can find this weight, we can represent circles. To begin with, we learn from geometry that the two legs of the control polygon must be equal, P0P1 = P1P2. Let the center and radius of the circle that is represented by the rational Bézier curve be O and r, respectively, as shown in the figure below. Let the mid-point of chord P0P2 be M, let the circle intersect the line segment MP1 at X, and let the angle at P1 be 2a. What we need to do is to find the value of |MX|/|MP1| = w/(1+w). From here, we can solve for w and the rational Bézier curve that defines this circle is completely determined.

From right triangle OMP0, we have |OM| = rsin(a), and, hence
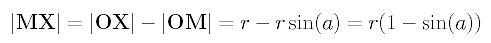
From right triangle OP0P1, we have OP1 = r/sin(a), and, hence MP1 can be computed as follows:
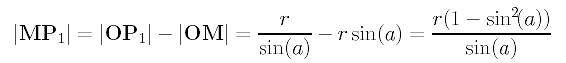
Now, we can compute w/(1+w) using |MX|/|MP1| and obtain the following result:
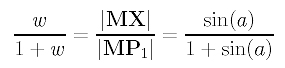
Solving for w, we have a surprisingly simple result: the only weight w is equal to the sine of the half angle at control point P1!
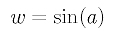
This means: given three control points P0, P1 and P2 such that P0P1 = P1P2 holds, if we choose w, the weight for P1, to be sin(a), where a is the half angle at control point P1, the resulting rational Bézier curve is a circle.
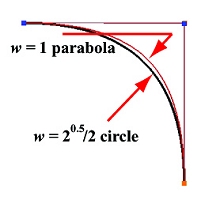
There are two very simple and commonly seen examples. The first is a quarter circle. The angle at P1 is 90 degree and a is 45 degree. Therefore, choosing w = sin(45 degree) = 20.5/2 yields a quarter circle. The figure below shows this quarter circle and the parabola that is defined by the same set of control point with w = 1.
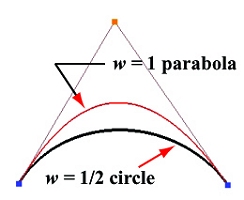
Our second example is 1/3 of a circle. Since a circle can be inscribed in an equilateral triangle, a triangle with all sides being equal, one-third of this circle has its opposite angle of 60 degree. Therefore, a is 30 degree. If we choose w to be sin(30 degree) = 1/2, we have this circular arc as shown below:
We can take three 1/3 circular arcs or four quarter circular arcs and piece them together to make a full circle as shown below. But, what are their representations? Of course, they must be NURBS curves of degree 2. What we need are the control points and knots.
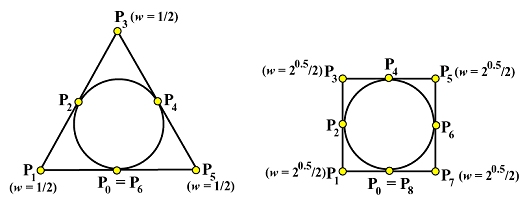
Let use consider the equilateral case first. This is shown in the left figure above. Each vertex of the equilateral is a control point with weight 1/2 as described earlier. The lower-left 1/3 is defined by control points P0, P1 and P2; the top 1/3 is defined by P2, P3 and P4; and the lower-right 1/3 is defined by P4, P5 and P6 = P0. This part is trivial. Next, we investigate the knots. Since n = 6 and p = 2, m = 6 + 2 + 1 (i.e., 10 knots). Of these 10 knots, the first three and last three are 0's and 1's, (i.e., u0 = u1 = u2 = 0, and u7 = u8 = u9 = 1). The unknown knots so far are u3, u4, u5 and u6. A natural way would be to have 1/3 and 2/3 as internal knots because the circular arcs on domains [0, 1/3], [1/3, 2/3] and [2/3, 1] divide the full circle into three equal length circular arcs. Thus, we have two more knots, and need two more.
Look at the figure and you will see that control point P2 lies on the circle at its 1/3 length. How do we force a curve to pass through a control point? This is what de Boor's algorithm does. When computing a point corresponding to u on a B-spline/NURBS curve, we insert u multiple times until the multiplicity of u is p, where p is the degree of the curve. The last time when u is inserted, the corresponding point on the curve is actually a (new) control point P2! This observation tells us that if 1/3 has a multiplicity 2, its corresponding point on the curve is a control point. In summary, we can have u3 = u4 = 1/3 and u5 = u6 = 2/3. In other words, to define a full circle using a equilateral, we have knots 0, 0, 0, 1/3, 1/3, 2/3, 2/3, 1, 1, 1! Similarly, to define a full circle with a square, we will need nine control points as shown in the figure, and knots, 0, 0, 0, 1/4, 1/4, 1/2, 1/2, 3/4, 3/4, 1, 1, 1. Based on this discussion, can you define a full circle using a regular polygon of n sides?