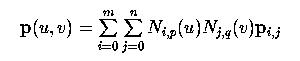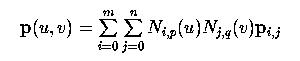B-spline Surfaces: Construction

Given the following information:
- a set of m+1 rows and n+1 control points
pi,j, where 0 <= i <= m and
0 <= j <= n;
- a knot vector of h + 1 knots in the u-direction,
U = { u0, u1, ....,
uh };
- a knot vector of k + 1 knots in the v-direction,
V = { v0, v1, ....,
vk };
- the degree p in the u-direction; and
- the degree q in the v-direction;
the B-spline surface defined by these information is the following:
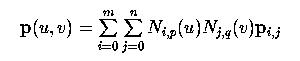
where Ni,p(u) and
Nj,q(v)
are B-spline basis functions of degree p and q, respectively.
Note that the fundamental identities, one for each direction,
must hold: h = m + p + 1 and k = n + q + 1.
Therefore, a B-spline surface is another example of tensor product surfaces.
As in Bézier surfaces, the set of control points is usually referred
to as the control net and the range of u and
v is 0 and 1. Hence, a B-spline surface maps the unit square to
a rectangular surface patch.
The following figure shows a B-spline surface defined by 6 rows and 6
columns of control points.

The knot vector and the degree in the u-direction are
U = { 0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1 } and 2. The knot vector and
the degree in the v-direction are
V = { 0, 0, 0, 0, 0.33, 0.66, 1, 1, 1, 1 } and 3.

Basis Functions
The coefficient of control point pi,j is the
product of two one-dimensional B-spline basis functions, one in the
u-direction, Ni,p(u), and the other
in the v-direction, Nj,q(v). All of
these products are two-dimensional B-spline functions. The following figures
show the basis functions of control points p2,0,
p2,1, p2,2, p2,3,
p2,4 and p2,5.






The two-dimensional basis functions are shown as wireframe surfaces. Since
the control points are on the same row, the basis function in the
u-direction is fixed while the basis functions in the
v-direction change. Since B-spline basis functions are in general
non-zero only on a few consecutive knot spans (i.e., the local
modification scheme), the two-dimensional B-spline basis functions are
non-zero on the product of two knot spans on which at least one
one-dimensional basis function is non-zero. This fact is shown in the
above figures clearly.

Clamped, Closed and Open B-spline Surfaces
Since a B-spline curve can be clamped, closed or open, a B-spline surface can
also have three types in each direction. That is, we could ask to
have a B-spline surface clamped in the u-direction and closed in the
v-direction. If a B-spline is clamped in both directions, then this
surface passes though control points p0,0,
pm,0, p0,n and
pm,n and is tangent to the eight legs of the control
net at these four control points. If a B-spline surface is closed in a
direction, then all isoparametric curves in this direction are closed curves
and the surface becomes a tube. If a B-spline surface is open in both
directions, then the surface does not pass through control points
p0,0, pm,0,
p0,n and pm,n. This set of
notes only concentrates on B-spline surfaces clamped in both
directions. The following figures show three B-spline surfaces clamped,
closed and open in both directions. All three surfaces are defined on the
same set of control points; but, as in B-spline curves, their knot vectors
are different.