|
|
|
|
|
|
| F3.2 | F3.6 | F4.0 | F4.5 | F5.0 |
|
|
|
|
|
|
| F5.6 | F6.4 | F7.1 | F8.0 | F9.0 |
| Click on the image to see a larger one | ||||
When a lens focuses on a subject at a distance, all subjects at that distance are sharply focused. Subjects that are not at the same distance are out-of-focus and theoretically are not sharp. However, since human eyes cannot distinguish very small degree of unsharpness, some subjects that are in front of and behind the in-focus subjects can still appear sharp. The zone of acceptable sharpness is referred to as the depth of field. Thus, increasing the depth of field increases the sharpness of an image. We can use smaller for increasing the depth of field.
The following shows an example. The lens focuses at the middle between the 3 inch and 4 inch marks. Thus, the 3 inch and 4 inch marks are sharp in all images. The 5 inch mark is not very sharp at F3.2, and its sharpness is improved as the lens closes down to F3.6. Then, it becomes sharp in all subsequent images. The 6 inch and 7 inch marks are not sharp until F5.0 and F6.4, respectively. The 8 inch mark becomes reasonably sharp when the lens closes down to F8.0. The 9 inch and 10 inch marks are not sharp in all images; but, they become sharper as the lens closes down. For the foreground, the 2 inch mark is acceptable at F3.2 and becomes in-focus at F4.0. The 1 inch mark is not sharp until F5.6, and the lead of the ruler becomes reasonably sharp at F7.1. As you can see, the range of sharpness (i.e., depth of field) gets larger as the aperture gets smaller. Therefore, use a smaller aperture if a greater depth of field is needed. Please check the Aperture-Priority Mode to learn more about the use of aperture and its impact on depth of field.
|
|
|
|
|
|
| F3.2 | F3.6 | F4.0 | F4.5 | F5.0 |
|
|
|
|
|
|
| F5.6 | F6.4 | F7.1 | F8.0 | F9.0 |
| Click on the image to see a larger one | ||||
Suppose the lens focuses on the yellow dot as shown in the figure below. This subject generates a yellow dot on the image plane. Once focused, all subjects that have the same subject-lens distance as that of the yellow dot will appear sharp. Now, consider a white dot that is behind the yellow dot (i.e., with larger subject-lens distance). Since it is out-of-focus, it will not produce a sharp white dot image. Instead, its image is formed somewhere in front of the image plane. On the image plane, the image of this white dot is a circle as shown below. This circle is usually referred to as a circle of confusion. As the subject-lens distance increases, the size of this circle increases. The same holds true for a subject in front of the yellow dot (e.g., the green dot in the figure below). Since these circles of confusion are actually out-of-focus images of dots, if we can reduce the size of circle of confusion, we can increase the sharpness of the resulting image. But, how?
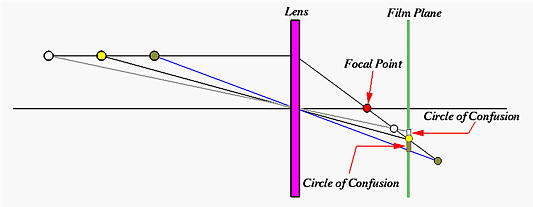
It turns out to be very simple. Since circles of confusion are formed by light rays passing through the lens tube, the size of a circle of confusion is proportional to the amount of light that can pass through the lens tube. This means smaller (resp., larger) circles of confusion will be formed if less (resp., more) light can pass through. Restricting how much light can pass through the lens is the function of aperture in the lens tube. Therefore, a smaller aperture means allowing less light to reach the image capturing device, which means we have smaller circles of confusion, and, as a result, we have a sharper image!
In addition to closing down the aperture, we can also focus at the hyperfocal distance to maximize depth of field. If a lens focuses at infinity, the depth of field starts at somewhere in front of the lens and extends to infinity. More precisely, from that point on, the scene appears sharp, and subjects between that point and the lens are out-of-focus. The distance from the lens to that point is referred to as the hyperfocal distance. In the figure below, the hyperfocal distance is marked with a thick red line.

After determining the hyperfocal distance, we can point the camera at this distance. The resulting depth of field starts from halfway of the hyperfocal distance and extends to infinity. This is, in fact, the maximum depth of field we can get. The concept is shown in the figure below.
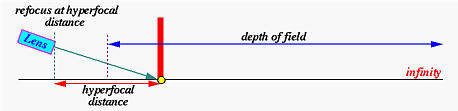
Why is this hyperfocal distance important? When shooting a distant subject or scene, many people point the camera to that subject(s). While the result may be satisfactory, in many cases the foreground looks out-of-focus. This is, of course, because of insufficient depth of field. Should this happen, the above technique becomes very useful: (1) focus at infinity; (2) determine the hyperfocal distance; (3) refocus at the hyperfocal distance; and (4) take a photo.
A ReminderHyperfocal distance is a function of the aperture being used. Changing aperture changes hyperfocal distance. |
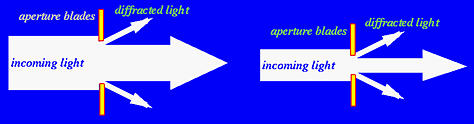
Unfortunately, in general, the answer is "no." As the light rays passing the lens tube and the aperture blades, some may be diffracted as shown in the figures below. If the aperture is large, because the proportion of the diffracted light and the non-diffracted light is so small and is negligible, diffraction does not contribute to the loss-of-quality very much. See the left figure below. However, when aperture is small, the amount of light that can pass through the aperture is reduced and hence the proportion of the diffracted and non-diffracted light becomes significant. As a result, the quality of the image is also reduced. See the right figure below. Therefore, closing the aperture all the way down to the smallest may not always increase the quality of an image. In general, the quality of a lens increases as the aperture closes down. This improvement will reach certain point. After this, quality goes down because of the impact of diffraction.
An Important NoteDiscussion in this section is based on an ideal lens and is somewhat simplified and theoretical. Since camera lenses are not perfect and may be different from manufacturer to manufacturer and even from lens to lens of the same type made by the same manufacture, depth of field calculation is not so simple. |
Recall from the concept of circle of confusion that the resolving power of human eyes is not very high, and, as a result, some sizes of circle of confusion may be perceived as perfect points. Thus, to understand the calculation of depth of field, we need to know what is the maximum size of circle of confusion that would be treated as a point by human eyes. Unfortunately, this maximum size, or diameter, of circle of confusion depends on so many factors. The most important fact is certainly the image size.
Suppose the same scene is recorded using two lenses, each of which is used on a camera with a different image size. If both lenses produce the same size of circle of confusion and both images are enlarged to the same size, then it is obvious that the smaller image requires higher magnification ratio to bring its size equal to that of the larger image. As a result, those circles of confusion recorded on the smaller image will become larger in the enlarged image than those from the larger image. Of course, the enlarged image from the smaller image will not look as sharp as the one from the larger image. This is why enlargements from large format camera always look sharper than the enlargements from smaller format cameras. Thus, this is the major reason that image size has to be a factor in the determination of the maximum size of circle of confusion.
A common way of incorporating image size into the calculation is to define the maximum diameter as follows:

Why standard lens? As we all know, a standard lens covers the same angle of view as human eyes. For example, the standard lens for a 35mm camera has a focal length of 50mm, while the corresponding focal length on a 995 is 10.5mm. Therefore, the maximum diameters of circle of confusion for 35mm and 995 are 50/1000=0.05 and 0.0105mm, respectively. Similarly, since 6×6 cm and 4×5 inch cameras have standard lens of focal lengths 80mm and 150mm, their maximum diameters of circle of confusion are 0.08mm and 0.15mm, respectively. On a Nikon D1, since its CCD size is smaller than a 35mm single frame, the lens factor is approximately 1.5. More precisely, a 35mm lens of focal length f becomes a lens of focal length 1.5*f for D1. As a result, the standard lens of D1 has focal length 50/1.5 = 33.3mm, and the diameter of maximum permissible circle of confusion is 0.033mm. It is suggested that for critical applications, multiply the above values by 0.6. Carl Zeiss even used 0.025 for 35mm lenses! In summary, we have the following table. In what follows, to simplify our calculation, we always use focal-length-of-standard-lens/1000 (i.e., 0.01mm for 990/995 and 0.05mm for 35mm).
| |
Diameter | |
| Format | General Use | Critical Application |
| 990/995 | 0.01mm | 0.006mm |
| 35mm | 0.05mm | 0.03mm |
| 6×6 cm | 0.08mm | 0.048mm |
| 4×5 inch | 0.15mm | 0.09mm |
The hyperfocal distance of a lens at a given focal length and aperture is calculated as follows. Note that the diameter of maximum permissible circle of confusion has to be chosen properly because the same lens used for a different image size gives a different diameter value.
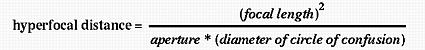
From this formula, we learn the following:
| Aperture | F2.8 | F5.6 | F8.0 | F11.0 |
| 995 @ 8mm | 2286 | 1143 | 800 | 582 |
| 35mm lens @ 38mm | 10314 | 5157 | 3610 | 2625 |
In fact, it is not difficult to verify that under this setting, the 35mm lens has a hyperfocal distance 4.5 times farther than that of 995. This explains partially that why images obtained with 995 always look sharper than those using 35mm lenses.
Depth of field is bounded by two distance measures: near and far, where near is the closest distance (to the camera) that subjects appear to be sharp and far is the shortest distance beyond which subjects look out-of-focus (or longest distance within which subjects appear to be in-focus). Thus, subjects with subject distances between near and far appear sharp on the resulting image. Of course, near must be less than far, and subject distances lies in between. The following shows the computation formulae.

Variables involved are focal length, subject distance (i.e., the distance between the subject and the camera), and hyperfocal distance. Note that aperture does not occur explicitly because it is used in the computation of hyperfocal distance. Therefore, we should not naively conclude that aperture is not used in the computation of depth of field.
There is one more important note. The subject distance does not have to be larger than the hyperfocal distance, because once we focus at the hyperfocal distance (i.e., subject distance = hyperfocal distance), we will have maximum depth of field, and near is half of the hyperfocal distance and far is at infinity.
Let us take a look at an example. Let the 995 use focal length 8mm (38mm, 35mm equivalent) at aperture F5.6. Note that the hyperfocal distance is 1143mm from the above table. If the lens is focused at 100mm (10cm), we have near = 48mm and far = 109mm; if the lens is focused at 1000mm (1m), we have near = 535mm and far = 7570mm. On the other hand, if the lens is a 35mm lens of focal length 38mm (equivalent to 995's 8mm) at the same aperture F5.6, the above table gives the hyperfocal distance 5157mm. If the lens is focused at 100mm (assuming it is possible), we have near = 99mm and far = 101mm; if the lens is focused at 1000mm, we have near = 842mm and far = 1229mm. The following table summarizes these information:
| |
Subject dist = 100mm | Subject Dist = 1000mm | ||||
| Camera | Near | Far | Length | Near | Far | Length |
| 995 @ 8mm and F5.6 | 48 | 109 | 61 | 535 | 7570 | 7035 |
| 35mm lens @ 38mm and F5.6 | 99 | 101 | 2 | 842 | 1229 | 387 |
| All values have unit mm |
From this table, it is easily seen that 995's short focal length produces a much longer area within which subjects appear sharp than an equivalent 35mm lens can produce. This is why images obtained from a 995 appear to be sharper. The crucial part is image size which makes the diameter of maximum permissible circle of confusion much smaller than the 35mm counterpart! This is also the reason that you cannot obtain a blurred background that is usually produced by a 35mm lens using larger apertures.