An ACM SIGCSE '99 Workshop

Time: Wednesday, March 24, 7:00PM to 10:00PM
Place: University of New Orleans Downtown campus

Teaching Curve and Surface Design in
Computer Graphics and Related Courses

Computer graphics instructors frequently skip the curves and surfaces chapters due to the problem of "too much mathematics". Fortunately, with our tools DesignMentor, we can take an intuitive approach, avoid the use of the involved mathematics, and get to the core of curve and surface design quickly. These tools have been classroom tested by our junior and senior students and the results have been very successful.

In this workshop all four types of parametric curves and surfaces (e.g., Bézier, rational Bézier, B-spline and NURBS) will be covered. Our discussion starts with the hierarchy of these curves and surfaces:

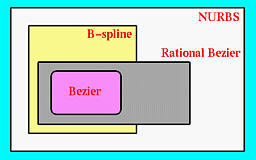
For each curve type, we shall discuss the meaning and the merit of its definition and important and fundamental properties:

• The definition of each curve.
• Important properties of each curve, which include the convex hull property, partition of unity, affine and/or projective invariance, local modification scheme and curve tracing. The following shows the computation steps of de Casteljau's and de Boor's algorithms for computing a point on a Bézier and a B-spline curve. The yellowish polygons are the convex hulls at a particular point on the curve and the line segments are the de Casteljau's and de Boor's nets.

• Basic shape modification techniques. These include changing the position of a control point, the value of the weight of a control point, and the value of a knot. The local modification scheme, which states that modifying the above mentioned quantities will only affect the curve locally, will also be discussed. The following figures show the effect of changing the position of a selected control point. It is clear that the left part of the curve does not change even though the position of the selected control point is changed drastically.
  

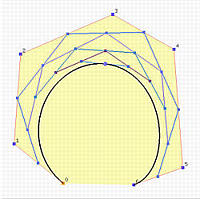
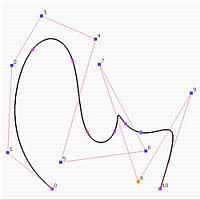
  The following shows the effect of changing the weight of a selected control point. The weight of the selected control point is 1. The left figure shows the result of increasing the weight to 5 (the curve is pulled toward the selected control point), and the right figure shows the result of decreasing the weight to 0.2 (the curve is pushed away from the selected control point).

  

• Fundamental algorithms. We shall discuss three extremely important fundamental algorithms, namely: knot insertion - inserting a new knot into the knot vector of a B-spline or a NURBS curve, degree elevation - increasing the degree of a curve by one, and curve subdivision - dividing a curve into two segments. These algorithms perform some modification to the defining parameters of a curve without changing its shape. The following shows the effect of inserting a new knot 0.25 into the knot vector of the left curve. The right figure is the result. Please note that the shape of the curve does not change. The only change is the three marked control points being replaced by four new control points.
  

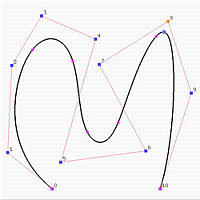
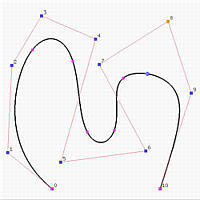
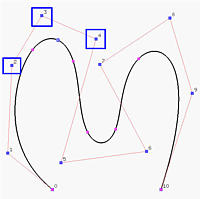
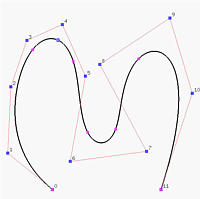
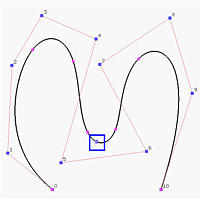
  The following shows the effect of subdividing the left curve at 0.45 into two curve segments, each of which has its own control points and knot vector. Thus, one can modify each component without affecting the other.

  

For the surface part, we shall start with the meaning of tensor product surfaces and focus on B-spline and NURBS surfaces. Almost all properties and algorithms for curves have natural and easy extensions to surfaces. For example, increasing (resp., decreasing) the weight of a selected control point will pull (resp., push) the surface toward (resp., away) from that control point. The following figures illustrate the effect of increasing the weight of the selected control point from 1 to 10. Both figures show the control points and control nets of the surfaces.

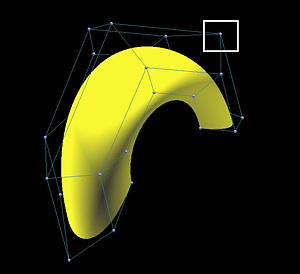
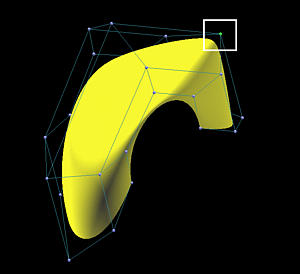
The most interesting application of the theory is the cross section technique. This technique reduces the design of a surface to the design of a few curves, and hence simplifies the whole design process. The cross section design technique requires one or more profile curves and a trajectory curve. The surface is constructed by sliding the profile curves, possibly with transformations (i.e., rotation and scaling), along the trajectory curve. Many classical surfaces can be constructed this way. This includes ruled surfaces, surfaces of revolution, swung surfaces and skinned surfaces. All of them will be discussed in some detail.

In our system, the input curves are NURBS ones and the output is a NURBS surface. The following shows the generation of a hyperboloid of one sheet as a ruled surface from two circles:

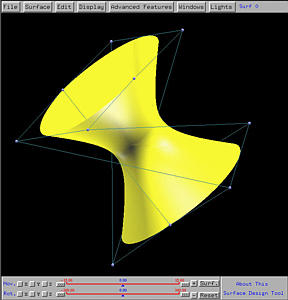
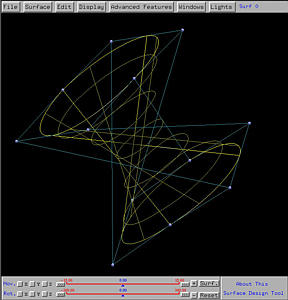
The following shows the construction of a vase as a surface of revolution from its profile curve:

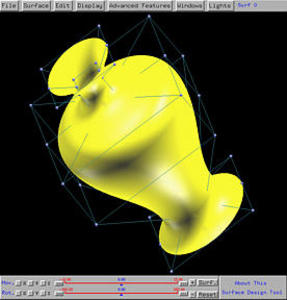
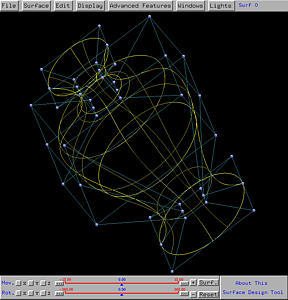
The following is a swung surface. It is constructed by swinging an up-side-down omega symbol about a squarish curve. As a result, the up-side-down omega curve provides the profile in the vertical direction, while the squarish curve gives the shape of the horizontal direction.

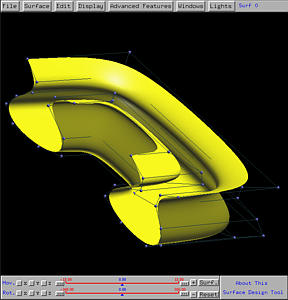
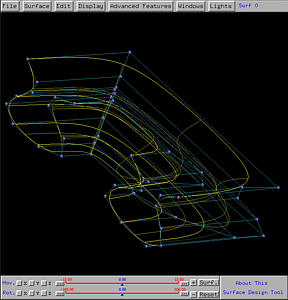
All figures shown on this page are screenshots of DesignMentor, which is available free and will be distributed at the workshop. If you are interested, please visit our site listed below to download a beta version. Currently, it is available on Sun, SGI and Linux (x86) platforms. Windows 95/NT versions are under development and will be available soon.

Check the following for additional information

Course Information: CS390 Introduction to Computing with Geometry

Curve System Manual

Surface System Manual

Visit the Geometric Computing Group and Download a Copy of DesignMentor

Author's Page

Dr. Ching-Kuang Shene

Dr. John L. Lowther

Other Pages

Michigan Technological University

Department of Computer Science

Department of Computer Science Course Information

Acknowledgments

This project and its accompanying software tools development are supported by the National Science Foundation under grant number CCR-9696084 (formerly CCR-9410707) and DUE-9653244, and by a Michigan Research Excellence Fund 1998-1999.

This page has been accessed times
since January 1, 1999.