Kasiski's Method

Kasiski suggested that one may look for repeated fragments in the ciphertext and compile a list of the distances that separate the repetitions. Then, the keyword length is likely to divide many of these distances. More precisely, Kasiski observed the following [KASISKI1863, KULLBACK1976}:

• If a repeated substring in a plaintext is encrypted by the same substring in the keyword, then the ciphertext contains a repeated substring and the distance of the two occurences is a multiple of the keyword length.
• Not every repeated string in the ciphertext arises in this way; but, the probability of a repetition by chance is noticeably smaller. See [POMMERENING2006] for a simple and interesting discussion.

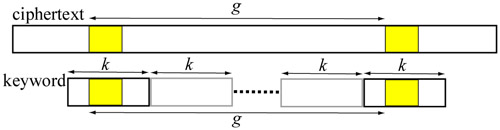
Consider the following example encrypted by the keyword ION. The substring BVR in the ciphertext repeats three times. The first two are encrypted from THE by ION. Since the keyword ION is shifted to the right repeatedly, the distance between the B in the first occurrence of BVR and the second is a multiple of the keyword length 3. The second and the third occurences of BVR tell a different story. They are encrypted from THE and NIJ using different portions of the keyword (i.e., ION and ONI) and the distance between the two B's in the second and third BVR may not be a multiple of the keyword length. Therefore, even we find repeated substrings, the distance between them may or may not be a multiple of the length of the keyword and the repetitions may just be purely by chance.

A long ciphertext may have a higher chance to see more repeated substrings and a short plaintext encrypted with relatively long keyword may produce a ciphertext in which no repetition can be found. Additionally, long repeated substrings in a ciphertext are not likely to be by chance, whereas short repeated substrings may appear more often and some of which may be purely by chance. The following example shows the encryption of Michigan Technological University with keyword boy. There is no repeated substring of length at least 2. Of course, Kasiski's method fails.

MICHI GANTE CHNOL OGICA LUNIV ERSIT Y
BOYBO YBOYB OYBOY BOYBO YBOYB OYBOY B
NWAIW EBBRF QFOCJ PUGDO JVBGW SPTWR Z

Consider a longer plaintext. The following is a quote from Charles Antony Richard Hoare (Tony Hoare or C. A. R. Hoare), the 1980 ACM Turing Award winner, on software design:

There are two ways of constructing a software design: 
One way is to make it so simple that there are obviously 
no deficiencies, and the other way is to make it so complicated 
that there are no obvious deficiencies. 
The first method is far more difficult.

After removing spaces and punctuation and converting to upper case, we have the following:

THERE ARETW OWAYS OFCON STRUC TINGA SOFTW AREDE SIGNO NEWAY 
ISTOM AKEIT SOSIM PLETH ATTHE REARE OBVIO USLYN ODEFI CIENC 
IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA 
RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF 
ICULT

Then, the above is encrypted with the 6-letter keyword SYSTEM as follows:

LFWKI MJCLP SISWK HJOGL KMVGU RAGKM KMXMA MJCVX WUYLG GIISW
ALXAE YCXMF KMKBQ BDCLA EFLFW KIMJC GUZUG SKECZ GBWYM OACFV
MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM
JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD
AVYXL

The following has the plaintext, keyword and ciphertext aligned together. The texts in blue mark the repeated substrings of length 8. These are the longest substrings of length less than 10 in the ciphertext. The plaintext string THEREARE appears three times at positions 0, 72 and 144. The distance between two occurences is 72. The repeated keyword and ciphertext are SYSTEMSY and LFWKIMJC, respectively. Therefore, these three occurences are not by chance and 72 is a multiple of the keyword length 6.

THERE ARETW OWAYS OFCON STRUC TINGA SOFTW AREDE SIGNO NEWAY
SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY
LFWKI MJCLP SISWK HJOGL KMVGU RAGKM KMXMA MJCVX WUYLG GIISW

ISTOM AKEIT SOSIM PLETH ATTHE REARE OBVIO USLYN ODEFI CIENC
STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST
ALXAE YCXMF KMKBQ BDCLA EFLFW KIMJC GUZUG SKECZ GBWYM OACFV

IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA
EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM
MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM

RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF
SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY
JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD

ICULT
STEMS
AVYXL

The next longest repeating substring WMLA in the ciphertext has length 4 and occurs at positions 108 and 182. The distance between these two positions is 74. At position 108, plaintext EOTH is encrypted to WMLA using SYST. At position 182, plaintext ETHO is encrypted to WMLA using STEM. In this case, even through we find repeating substrings WMLA, they are not encrypted by the same portion of the keyword and they come from different plaintext sections. As a result, this repetition is a pure chance and the distance 74 is unlikely to be a multiple of the keyword length.

IESAN DTHEO THERW AYIST OMAKE ITSOC OMPLI CATED THATT HEREA
EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY STEMS YSTEM
MQKYF WXTWM LAIDO YQBWF GKSDI ULQGV SYHJA VEFWB LAEFL FWKIM

RENOO BVIOU SDEFI CIENC IESTH EFIRS TMETH ODISF ARMOR EDIFF
SYSTE MSYST EMSYS TEMSY STEMS YSTEM SYSTE MSYST EMSYS TEMSY
JCFHS NNGGN WPWDA VMQFA AXWFZ CXBVE LKWML AVGKY EDEMJ XHUXD

ICULT
STEMS
AVYXL

There are five repeating substrings of length 3. They are MJC at positions 5 and 35 with a distance of 30, ISW at positions 11 and 47 (distance = 36), KMK at positions 28 and 60 (distance = 32), VMQ at positions 99 and 165 (distance = 66), and DAV at positions 163 and 199 (distance = 36). The following table is a summary. Note that the repeating ciphertext KWK is encrypted from two plaintext sections GAS and SOS with keyword portions of EMS and SYS, respectively. Therefore, this is a pure chance.

The following table shows the distances and their factors. Since a distance may be a multiple of the keyword length, a factor of a distance may be the length of the keyword. If a match is by pure chance, the factors of this distance may not be factors of the keyword length. In general, a good choice is the largest one that appears most often. Note that longer repeating substrings may offer better choices because these matches are less likely to be by chance.

The following table shows the distances and all factors no higher than 20. The last row of the table has the total count of each factor. It is clear that factors 2, 3 and 6 occur most often with counts 6, 4 and 4, respectively. Since keyword length 2 is too short to be used effectively, lengths 3 and 6 are more reasonable. As a result, we may use 3 and 6 as the initial estimates to recover the keyword and decrypt the ciphertext.

If we are convinced that some distances are likely not to be by chance, we may compute the greatest common divisor (GCD) of these distances and use it as a possible keyword length. As mentioned earlier, distances 74 and 32 are likely to be by chance and the remaining distances are 72, 66, 36 and 30. Their GCD is GCD(72, 66, 36, 30) = 6. Since we know the keyword SYSTEM, 6 is the correct length. If we only have a ciphertext in hand, we have to do some guess work.

Example 1

VVQGY TVVVK ALURW FHQAC MMVLE HUCAT WFHHI PLXHV UWSCI GINCM
UHNHQ RMSUI MHWZO DXTNA EKVVQ GYTVV QPHXI NWCAB ASYYM TKSZR
CXWRP RFWYH XYGFI PSBWK QAMZY BXJQQ ABJEM TCHQS NAEKV VQGYT
VVPCA QPBSL URQUC VMVPQ UTMML VHWDH NFIKJ CPXMY EIOCD TXBJW
KQGAN

A search reveals the following repeating substrings and distances:

The following table shows the distances and their factors. The most common factors between 2 and 20 are 3, 4, 6, 8 and 9. They all appear to be reasonable and other methods may be needed to narrow down the choice. Note that 2 is excluded because it is too short for pratical purpose. ♦

References

• [KASISKI1863] Friedrich W. Kasiski, Die Geheimschriften und die Dechiffrirkunst, Mittler und Sohn, Berlin, 1863. (An unabridged facsimile version was published by Adamant Media Corporation in 2006.)
• [KULLBACK1976] Solomon Kullback, Statistical Methods in Cryptanalysis, Aegean Park Press, 1976. (This book was originally published in 1938 by the Government Printing Office.)
• [POMMERENING2006] Klaus Pommerening, Kasiski's Test: Couldn't the Repetitions be by Accident?, Cryptologia, Vol. 30 (2006), No. 4 (October), pp. 346-352.