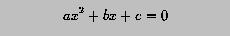
Given a quadratic equation as follows:
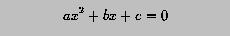
if b*b-4*a*c is non-negative, the roots of the equation can be solved with the following formulae:
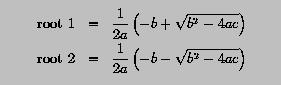
Write a program to read in the coefficients a, b and c, and compute and display the roots. If the discriminant b*b - 4*a*c is negative, the equation has complex root. Thus, this program should solve the equation if the discriminant is non-negative and show a message otherwise.
![]()
! ---------------------------------------------------
! Solve Ax^2 + Bx + C = 0 given B*B-4*A*C >= 0
! Now, we are able to detect complex roots.
! ---------------------------------------------------
PROGRAM QuadraticEquation
IMPLICIT NONE
REAL :: a, b, c
REAL :: d
REAL :: root1, root2
! read in the coefficients a, b and c
READ(*,*) a, b, c
WRITE(*,*) 'a = ', a
WRITE(*,*) 'b = ', b
WRITE(*,*) 'c = ', c
WRITE(*,*)
! compute the square root of discriminant d
d = b*b - 4.0*a*c
IF (d >= 0.0) THEN ! is it solvable?
d = SQRT(d)
root1 = (-b + d)/(2.0*a) ! first root
root2 = (-b - d)/(2.0*a) ! second root
WRITE(*,*) 'Roots are ', root1, ' and ', root2
ELSE ! complex roots
WRITE(*,*) 'There is no real roots!'
WRITE(*,*) 'Discriminant = ', d
END IF
END PROGRAM QuadraticEquation
Click here to download this program.
1.0 5.0 2.0 a = 1. b = 5. c = 2. Roots are -0.438447237 and -4.561553
1.0 2.0 5.0 a = 1. b = 2. c = 5. There is no real roots! Discriminant = -16.
| b*b - 4.0*a*c >= 0.0 | computes the real roots |
| there is no real roots |