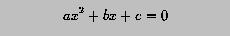
Quadratic Equation Solver - Revisited

Problem Statement

Given a quadratic equation as follows:

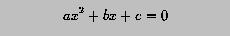
if b*b-4*a*c is non-negative, the roots of the equation can be solved with the following formulae:

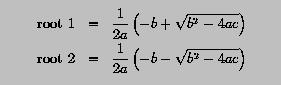
Write a program to read in the coefficients a, b and c, and solve the equation. Note that a quadratic equation has repeated root if b*b-4.0*a*c is equal to zero.

However, if a is zero, the equation becomes a linear one whose only solution is -c/b if b is not zero. Otherwise, if b is zero, two cases are possible. First, if c is also zero, any number can be a solution because all three coefficients are zero. Otherwise, the equation c = 0 cannot have any solution.

This program should handle all cases.

Solution

! ---------------------------------------------------
!   Solve  Ax^2 + Bx + C = 0 given B*B-4*A*C >= 0
!   Now, we are able to detect the following:
!    (1) unsolvable equation
!    (2) linear equation
!    (3) quadratic equation
!        (a) distinct real roots
!        (b) repeated root
!        (c) no real roots
! ---------------------------------------------------

PROGRAM  QuadraticEquation
   IMPLICIT  NONE

   REAL  :: a, b, c
   REAL  :: d
   REAL  :: root1, root2

!  read in the coefficients a, b and c

   READ(*,*)  a, b, c
   WRITE(*,*) 'a = ', a
   WRITE(*,*) 'b = ', b
   WRITE(*,*) 'c = ', c
   WRITE(*,*)

   IF (a == 0.0) THEN              ! could be a linear equation
      IF (b == 0.0) THEN           ! the input becomes c = 0
         IF (c == 0.0) THEN        ! all numbers are roots
            WRITE(*,*)  'All numbers are roots'
         ELSE                      ! unsolvable
            WRITE(*,*)  'Unsolvable equation'
         END IF
      ELSE                         ! linear equation
         WRITE(*,*)  'This is linear equation, root = ', -c/b
      END IF
   ELSE                            ! ok, we have a quadratic equation
      d = b*b - 4.0*a*c
      IF (d > 0.0) THEN            ! distinct roots?
         d     = SQRT(d)
         root1 = (-b + d)/(2.0*a)  ! first root
         root2 = (-b - d)/(2.0*a)  ! second root
         WRITE(*,*)  'Roots are ', root1, ' and ', root2
      ELSE IF (d == 0.0) THEN      ! repeated roots?
         WRITE(*,*)  'The repeated root is ', -b/(2.0*a)
      ELSE                         ! complex roots
         WRITE(*,*)  'There is no real roots!'
         WRITE(*,*)  'Discriminant = ', d
      END IF
   END IF

END PROGRAM  QuadraticEquation

Click here to download this program.

Program Input and Output

Since we have been doing the quadratic part in several similar examples, the following concentrates on the order part of the program.

If the input to the program consists of 0.0, 1.0 and 5.0, we have the following output. Since a is zero, this could be a linear equation. Since b=1.0, it is a linear equation 1.0*x + 5.0 = 0.0 with the only root -5.0/2.0=-5.0.
```
0.0  1.0  5.0

a = 0.E+0
b = 1.
c = 5.

This is linear equation, root = -5.
```
If the input to the program consists of 0.0, 0.0 and 0.0, we have the following output. Since all coefficients are zero, any number is a root.
```
0.0  0.0  0.0

a = 0.E+0
b = 0.E+0
c = 0.E+0

All numbers are roots
```
If the input to the program consists of 0.0, 0.0 and 4.0, we have the following output. Since the equation becomes 4.0 = 0.0, which is impossible. Therefore, this is not a solvable equation.
```
0.0  0.0  4.0

a = 0.E+0
b = 0.E+0
c = 4.

Unsolvable equation
```

Discussion

Here is the box trick of this program. It is more complex than all previous versions of quadratic equation solvers.

Let us start with linear equations.

a = 0	it could be a linear equation
	a quadratic equation

Since we have learned to do the quadratic part, we shall do the linear equation part first. To be a linear equation, b cannot be zero and this has to be addressed in the upper rectangle:

a = 0	b = 0	need to know if c is zero
		the equation is linear *bx+c=0**
	a quadratic equation

If c is zero, then every number is a root and we have:

a = 0	b = 0	c = 0	every number is a root
			this equation is not solvable
		the equation is linear *bx+c=0**
	a quadratic equation

To complete the bottom rectangle, let us take the box from previous example. The final result is:

a = 0	b = 0	c = 0	every number is a root
			this equation is not solvable
		the equation is linear *bx+c=0**
	*bb - 4.0ac ? 0.0**	>	computes the real roots
		=	computes the repeated root
		>	no real root

The above program is written based on this logic.