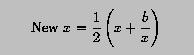
Computing the Square Root of a Positive Number

Problem Statement

The square root of a positive number b can be computed with Newton's formula:

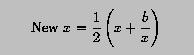
where x above starts with a "reasonable" guess. In fact, you can always start with b or some other value, say 1.

With b and a guess value x, a new guess value is computed with the above formula. This process continues until the new guess value and the current guess value are very close. In this case, either one can be considered as an approximation of the square root of b.

Write a program that reads in a REAL value and a tolerance, and computes the square root until the absolute error of two adjacent guess values is less than the tolerance value.

Solution

! ---------------------------------------------------------
! This program uses Newton's method to find the square
! root of a positive number.  This is an iterative method
! and the program keeps generating better approximation
! of the square root until two successive approximations
! have a distance less than the specified tolerance.
! ---------------------------------------------------------

PROGRAM  SquareRoot
   IMPLICIT  NONE

   REAL    :: Input, X, NewX, Tolerance
   INTEGER :: Count

   READ(*,*)  Input, Tolerance

   Count = 0                            ! count starts with 0
   X     = Input                        ! X starts with the input value
   DO                                   ! for each iteration
      Count = Count + 1                 !    increase the iteration count
      NewX  = 0.5*(X + Input/X)         !    compute a new approximation
      IF (ABS(X - NewX) < Tolerance)  EXIT   ! if they are very close, exit
      X = NewX                          !    otherwise, keep the new one
   END DO

   WRITE(*,*)  'After ', Count, ' iterations:'
   WRITE(*,*)  '  The estimated square root is ', NewX
   WRITE(*,*)  '  The square root from SQRT() is ', SQRT(Input)
   WRITE(*,*)  '  Absolute error = ', ABS(SQRT(Input) - NewX)

END PROGRAM  SquareRoot

Click here to download this program.

Program Input and Output

If the input are 10.0 for b and 0.00001 for the tolerance, the following output shows that it requires 6 iterations to reach an approximation of square root of 10. Comparing the result with the one obtained from Fortran intrinsic function SQRT(), the absolute error is zero.

After 6 iterations:
  The estimated square root is 3.1622777
  The square root from SQRT() is 3.1622777
  Absolute error = 0.E+0

If the input are 0.5 for b and 0.00001 for the tolerance, it takes 4 iterations to reach an approximation of the square root of 0.5. The value from using Fortran intrinsic function SQRT() is 0.707106769 and again the absolute error is 0.

After 4 iterations:
  The estimated square root is 0.707106769
  The square root from SQRT() is 0.707106769
  Absolute error = 0.E+0

Discussion

This program uses X to hold the input value for b and uses NewX to hold the new guess value. The initial guess is the input value.
From the current guess, using Newton's formula, the new guess is compared as
```
NewX  = 0.5*(X + Input/X)
```
Then, the absolute error of X and NewX is computed. If it is less than the tolerance value, EXIT the loop and display the results. Otherwise, the current guess is replaced with the new guess and go back for the next iteration.