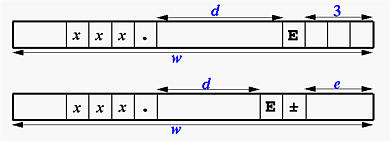
REAL Output: The E Descriptor

The Ew.d and Ew.dEe descriptors are for
REAL output. The printed numbers will be in an exponential form.
The general form of these descriptors are discussed below. There are two
more forms, ESw.d and
ENw.d, which will be discussed at the
bottom of this page.
rEw.d and
rEw.dEe
The meaning of r, w, d and
e are:
- E is for REAL numbers in exponential forms.
- w is the width of field, which indicates that
a real number should be printed with w positions.
- To print a number in an exponential form, it is first converted to
a normalized form
s0.xxx...xxx×10sxx,
where s is the sign of the number and the
exponent and x is a digit. For example,
12.345, -12.345, 0.00123 and -0.00123
are converted to 0.12345×102,
-0.12345×102, 0.123×10-2 and
-0.123×10-2.
- The Ew.d descriptor generates real numbers in
the following form:

Of these w positions, the last three are for the
exponent, including its sign, the middle d
positions are for the number in normalized form. Therefore,
excluding the exponent part, there are w-4
positions for printing the digits of the normalized number.
In fact, you can consider the normalized number is printed with
Fw-4.d. The above figure also includes
a 0 and a decimal point. If the number is negative, we
must also include its sign. Hence, 4+3=7 positions are not
available for printing the normalized number and, as a result,
when you use the E edit descriptor,
w must be greater than or
equal to d+7; otherwise, your number
may not be printed properly and all w positions will
be filled with asterisks.
- The Ew.dEe descriptor generates real numbers
in the following form:

As you can see, the only difference is that the exponent part now
has e positions. If your data has an exponent
larger than 99 or less than -99, Ew.d will not be
able to print it properly because there are only two positions
for the exponent (therefore, all w positions will
be filled with asterisks). As shown in the figure, in
addition to the d positions for the normalized
number and e positions for the exponent, we need
four more positions for printing the sign in the exponent,
a decimal point, a leading 0 and the character E.
Moreover, if the number is negative, a sign before the 0
is needed. This means that
w must be greater than or equal to
d+e+5.
- r is the repetition indicator, which gives
the number of times the edit descriptor should be repeated.
For example, 3E20.7E2 is equivalent to
E20.7E2, E20.7E2, E20.7E2.

Examples
In the following table, the WRITE statements use different E
edit descriptors to print the value of 3.1415926. The
WRITE statements are shown in the left and their corresponding
output, all using 12 positions, are shown in the right.

- The first example uses E12.5 to print 3.1415926.
This number is first converted to 0.31415926×101.
Therefore, the normalized number is 0.31415926 and the exponent
is 1. The exponent part is printed as E+01.
Since we have only 5 positions for printing 0.31415926 which has
8 digits, the sixth one will be rounded to the fifth and the
result is 0.31416.
- The second example uses E12.3E4 to print the same number.
This E descriptor indicates that four positions are for
the exponent and, as a result, the printed exponent part is
E+0001.
- The last example is obvious. However, if the number is
changed to -3.1415926, the result will be 12 asterisks, since
there is no position for the sign of the number.

Editor Descriptor ESw.d and
ESw.dEe
Scientists write the exponential form in a slightly different way.
This ES edit descriptor is for printing a real number in scientific
form, which has a non-zero digit as the integral part. If the number is a
zero, then all digits printed will be zero. The following shows the
printed form:
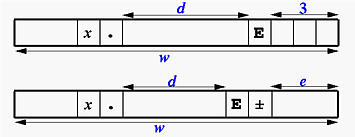
If you understand the form of normalized number, you can just shift the
decimal point to the right one position and decrease the exponent by one.
The result is in scientific form.
For example, if the number is 34.5678, it has a normalized form
0.345678×102. Now shifting the decimal point to the right
one position gives 3.45678×101. The following shows the
output printed with ES12.3E3:


Editor Descriptor ENw.d and
ENw.dEe
Engineers write the exponential form in yet another way. In an engineering
form, the exponent is always a multiple of three, and the printed number
always has no more than three and at least one non-zero digits. For
example, suppose the given number is 1234.567. The integral part has
four digits and the exponent is zero. To convert this number to an
engineering form, the decimal point should be shifted to the left three
positions. Thus, the given number has a new form
1.234567×103. Similarly, if the given number is
0.00001234567, shifting the decimal point to the right three positions
gives 0.01234567×10-3. However, this is not yet in the
engineering form, because the integral part is still zero. Therefore,
we need to shift the decimal point to the right three positions again and
this gives 12.34567×10-6. Now, the number is in
engineering form.
The following shows the output of ENw.d and
ENw.dEe. For ENw.d, it requires
4 positions for the exponent, d positions for the fractional
part of the number, 3 positions for the integral part, one position for the
decimal point, and one position for the possible sign. It requires
at least d+9 positions and consequently
for ENw.d, w must be
larger than or equal to d+9. The same counting
yields that for ENw.dEe,
w must be larger than or equal to d+e+7
.