Heron's Formula for Computing Triangle Area - Revisited

Problem Statement

Given a triangle with side lengths a, b and c, its area can be computed using the Heron's formula:

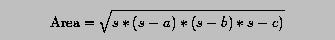
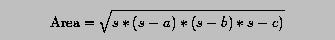
where s is the half of the perimeter length:

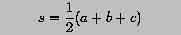
In order for a, b and c to form a triangle, two conditions must be satisfied. First, all side lengths must be positive:

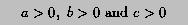
Second, the sum of any two side lengths must be greater than the third side length:

Write a program to read in three real values and use a function for testing the conditions and another function for computing the area. Should the conditions fail, your program must keep asking the user to re-enter the input until the input form a triangle. Then, the other function is used to compute the area.

Solution 

! --------------------------------------------------------------------
!    This program uses Heron's formula to compute the area of a
! triangle.  It "contains" the following functions;
!    (1)  LOGICAL function TriangleTest() -
!         this function has three real formal arguments and tests
!         to see if they can form a triangle.  If they do form a
!         triangle, this function returns .TRUE.; otherwise, it
!         returns .FALSE.
!    (2)  REAL function TriangleArea() -
!         this functions has three real formal arguments considered
!         as three sides of a triangle and returns the area of this
!         triangle.
! --------------------------------------------------------------------

PROGRAM  HeronFormula
   IMPLICIT  NONE

   REAL :: a, b, c, TriangleArea

   DO
      WRITE(*,*)  'Three sides of a triangle please --> '
      READ(*,*)   a, b, c
      WRITE(*,*)  'Input sides are ', a, b, c
      IF (TriangleTest(a, b, c))  EXIT  ! exit if not a triangle
      WRITE(*,*)  'Your input CANNOT form a triangle.  Try again'
   END DO

   TriangleArea = Area(a, b, c)
   WRITE(*,*)  'Triangle area is ', TriangleArea

CONTAINS

! --------------------------------------------------------------------
! LOGICAL FUNCTION  TriangleTest() :
!    This function receives three REAL numbers and tests if they form
! a triangle by testing:
!    (1)  all arguments must be positive, and
!    (2)  the sum of any two is greater than the third
! If the arguments form a triangle, this function returns .TRUE.;
! otherwise, it returns .FALSE.
! --------------------------------------------------------------------

   LOGICAL FUNCTION  TriangleTest(a, b, c)
      IMPLICIT  NONE

      REAL, INTENT(IN) :: a, b, c
      LOGICAL          :: test1, test2

      test1 = (a > 0.0) .AND. (b > 0.0) .AND. (c > 0.0)
      test2 = (a + b > c) .AND. (a + c > b) .AND. (b + c > a)
      TriangleTest = test1 .AND. test2  ! both must be .TRUE.
   END FUNCTION  TriangleTest

! --------------------------------------------------------------------
! REAL FUNCTION  Area() :
!    This function takes three real number that form a triangle, and
! computes and returns the area of this triangle using Heron's formula.
! --------------------------------------------------------------------

   REAL FUNCTION  Area(a, b, c)
      IMPLICIT  NONE

      REAL, INTENT(IN) :: a, b, c
      REAL             :: s

      s    = (a + b + c) / 2.0
      Area = SQRT(s*(s-a)*(s-b)*(s-c))
   END FUNCTION  Area

END PROGRAM  HeronFormula
Click here to download this program.

Program Input and Output

The following is the output from the above program. 
Three sides of a triangle please -->
-3.0  4.0  5.0
Input sides are -3.,  4.,  5.
Your input CANNOT form a triangle.  Try again
Three sides of a triangle please -->
1.0  3.0  4.0
Input sides are 1.,  3.,  4.
Your input CANNOT form a triangle.  Try again
Three sides of a triangle please -->
6.0  8.0  10.0
Input sides are 6.,  8.,  10.
Triangle area is 24.

Discussion