Heron's Formula for Computing Triangle Area Using External Functions

Problem Statement

We have seen Heron's formula for computing triangle area using internal functions. This problem uses the same idea; but the program should use an internal subroutine.

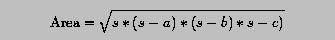
Given a triangle with side lengths a, b and c, its area can be computed using the Heron's formula:

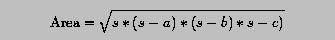
where s is the half of the perimeter length:

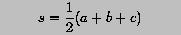
In order for a, b and c to form a triangle, two conditions must be satisfied. First, all side lengths must be positive:

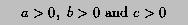
Second, the sum of any two side lengths must be greater than the third side length:

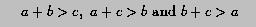
Write a program to read in three real values and use an internal subroutine to compute the triangle area. This subroutine should tell the main program if the area computation is successful.

Solution 

! --------------------------------------------------------------------
! PROGRAM  HeronFormula:
!    This program contains one subroutine that takes three REAL values
! and computes the area of the triangle bounded by the input values.
! --------------------------------------------------------------------

PROGRAM  HeronFormula
   IMPLICIT  NONE

   REAL    :: Side1, Side2, Side3       ! input values
   REAL    :: Answer                    ! will hold the area
   LOGICAL :: ErrorStatus               ! return status

   READ(*,*)  Side1, Side2, Side3
   CALL  TriangleArea(Side1, Side2, Side3, Answer, ErrorStatus)
   IF (ErrorStatus) THEN                ! if error occurs in subroutine
      WRITE(*,*)  "ERROR: not a triangle"    ! display a message
   ELSE                                 ! otherwise, display the area
      WRITE(*,*)  "The triangle area is ", Answer
   END IF

CONTAINS

! --------------------------------------------------------------------
! SUBROUTINE  TriangleArea():
!    This subroutine takes three REAL values as the sides of a
! triangle.  Then, it tests to see if these values do form a triangle.
! If they do, the area of the triangle is computed and returned with
! formal argument Area and .FALSE. is returned with Error.  Otherwise,
! the area is set to 0.0 and .TRUE. is returned with Error.
! --------------------------------------------------------------------

   SUBROUTINE  TriangleArea(a, b, c, Area, Error)
      IMPLICIT  NONE

      REAL, INTENT(IN)     :: a, b, c   ! input sides
      REAL, INTENT(OUT)    :: Area      ! computed area
      LOGICAL, INTENT(OUT) :: Error     ! error indicator

      REAL                 :: s
      LOGICAL              :: Test1, Test2

      Test1 = (a > 0) .AND. (b > 0) .AND. (c > 0)
      Test2 = (a+b > c) .AND. (a+c > b) .AND. (b+c > a)
      IF (Test1 .AND. Test2) THEN       ! a triangle?
         Error = .FALSE.                ! yes.  no error
         s     = (a + b + c)/2.0        ! compute area
         Area  = SQRT(s*(s-a)*(s-b)*(s-c))
      ELSE
         Error = .TRUE.                 ! not a triangle
         Area  = 0.0                    ! set area to zero
      END IF
   END SUBROUTINE  TriangleArea

END PROGRAM  HeronFormula
Click here to download this program.

Program Input and Output

The following is the output from the above program for input 3.0, 5.0 and 7.0. 
The triangle area is 6.49519062

Discussion