Computing Means - Revisited (Again)

Problem Statement

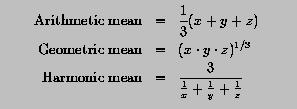
The arithmetic, geometric and harmonic means of three positive numbers are defined by the following formulas:

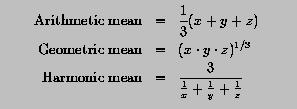
Write a program to read three positive numbers and use a single internal subroutine to compute the arithmetic, geometric and harmonic means.

Solution

! ----------------------------------------------------------
!    This program contains one subroutine for computing the
! arithmetic, geometric and harmonic means of three REALs.
! ----------------------------------------------------------

PROGRAM  Mean6
   IMPLICIT  NONE

   REAL :: u, v, w
   REAL :: ArithMean, GeoMean, HarmMean

   READ(*,*)  u, v, w

   CALL  Means(u, v, w, ArithMean, GeoMean, HarmMean)

   WRITE(*,*) "Arithmetic Mean = ", ArithMean
   WRITE(*,*) "Geometric Mean  = ", GeoMean
   WRITE(*,*) "Harmonic Mean   = ", HarmMean

CONTAINS

! ----------------------------------------------------------
! SUBROUTINE  Means():
!    This subroutine receives three REAL values and computes
! their arithmetic, geometric, and harmonic means.
! ----------------------------------------------------------

   SUBROUTINE  Means(a, b, c, Am, Gm, Hm)
      IMPLICIT  NONE

      REAL, INTENT(IN)  :: a, b, c
      REAL, INTENT(OUT) :: Am, Gm, Hm

      Am = (a + b + c)/3.0
      Gm = (a * b * c)**(1.0/3.0)
      Hm = 3.0/(1.0/a + 1.0/b + 1.0/c)
   END SUBROUTINE  Means

END PROGRAM  Mean6

Program Input and Output

Arithmetic Mean = 5.66666651
Geometric Mean  = 5.24148321
Harmonic Mean   = 4.80000019