Computing Mean, Variance and Standard Deviation

Problem Statement

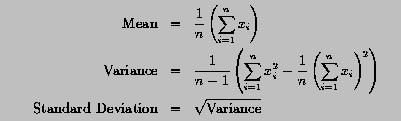
Given n data items x1, x2, ..., xn, the mean, variance and standard deviation of these data items are defined as follows:

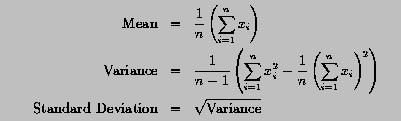
Write a program that reads in an unknown number of data items, one on each line, counts the number of input data items and computes their mean, variance and standard deviation.

Solution

! --------------------------------------------------------------------
! PROGRAM  MeanVariance:
!    This program reads in an unknown number of real values and
! computes its mean, variance and standard deviation.  It contains
! three subroutines:
!    (1)  Sums()     - computes the sum and sum of squares of the input
!    (2)  Result()   - computes the mean, variance and standard
!                      deviation from the sum and sum of squares
!    (3)  PrintResult() - print results
! --------------------------------------------------------------------

PROGRAM  MeanVariance
   IMPLICIT   NONE

   INTEGER :: Number, IOstatus
   REAL    :: Data, Sum, Sum2
   REAL    :: Mean, Var, Std

   Number = 0                           ! initialize the counter
   Sum    = 0.0                         ! initialize accumulators
   Sum2   = 0.0

   DO                                   ! loop until done
      READ(*,*,IOSTAT=IOstatus)  Data   ! read in a value
      IF (IOstatus < 0)  EXIT           ! if end-of-file reached, exit
      Number = Number + 1               ! no, have one more value
      WRITE(*,*)  "Data item ", Number, ": ", Data
      CALL  Sums(Data, Sum, Sum2)       ! accumulate the values
   END DO

   CALL  Results(Sum, Sum2, Number, Mean, Var, Std)  ! compute results
   CALL  PrintResult(Number, Mean, Var, Std)         ! display them

CONTAINS

! --------------------------------------------------------------------
! SUBROUTINE  Sums():
!    This subroutine receives three REAL values:
!    (1)  x      - the input value
!    (2)  Sum    - x will be added to this sum-of-input
!    (3)  SumSQR - x*x is added to this sum-of-squares
! --------------------------------------------------------------------

   SUBROUTINE  Sums(x, Sum, SumSQR)
      IMPLICIT  NONE
      REAL, INTENT(IN)    :: x
      REAL, INTENT(INOUT) :: Sum, SumSQR

      Sum    = Sum + x
      SumSQR = SumSQR + x*x
   END SUBROUTINE  Sums

! --------------------------------------------------------------------
! SUBROUTINE  Results():
!    This subroutine computes the mean, variance and standard deviation
! from the sum and sum-of-squares:
!    (1) Sum       - sum of input values
!    (2) SumSQR    - sun-of-squares
!    (3) n         - number of input data items
!    (4) Mean      - computed mean value
!    (5) Variance  - computed variance
!    (6) StdDev    - computed standard deviation
! --------------------------------------------------------------------

   SUBROUTINE  Results(Sum, SumSQR, n, Mean, Variance, StdDev)
      IMPLICIT  NONE

      INTEGER, INTENT(IN) :: n
      REAL, INTENT(IN)    :: Sum, SumSQR
      REAL, INTENT(OUT)   :: Mean, Variance, StdDev

      Mean = Sum / n
      Variance = (SumSQR - Sum*Sum/n)/(n-1)
      StdDev   = SQRT(Variance)
   END SUBROUTINE

! --------------------------------------------------------------------
! SUBROUTINE  PrintResults():
!    This subroutine displays the computed results.
! --------------------------------------------------------------------

   SUBROUTINE  PrintResult(n, Mean, Variance, StdDev)
      IMPLICIT  NONE

      INTEGER, INTENT(IN) :: n
      REAL, INTENT(IN)    :: Mean, Variance, StdDev

      WRITE(*,*)
      WRITE(*,*) "No. of data items  = ", n
      WRITE(*,*) "Mean               = ", Mean
      WRITE(*,*) "Variance           = ", Variance
      WRITE(*,*) "Standard Deviation = ", StdDev
   END SUBROUTINE  PrintResult

END PROGRAM  MeanVariance

Program Input and Output

Data item 1: 5.
Data item 2: 2.
Data item 3: 6.
Data item 4: 8.
Data item 5: 4.5
Data item 6: 7.

No. of data items  = 6
Mean               = 5.41666651
Variance           = 4.44166565
Standard Deviation = 2.10752606

Discussion

• The mean program has a DO-EXIT-END DO. For each iteration, an input value is read into Data. Note that IOSTAT= is used in the READ statement. Thus, if the value of IOstatus is negative, end-of-file is reached and the execution exits the DO-loop. Otherwise, the main program calls subroutine Sums() to add the input value Data to Sum and the square of Data to Sum2.

  After reaching the end of file, the EXIT brings the execution to the second CALL. It calls subroutine Results() to compute the mean, variance and standard deviation from Sum and Sum2.

  Finally, subroutine PrintResult() is called to display the result.

• Subroutine Sums() receives an input value from x and adds its value to Sum and its square to SumSQR. Why are Sum and SumSQR declared with INTENT(INOUT)?
• Subroutine Results() computes the mean, variance and standard deviation using Sum, SumSQR and n.
• Subroutine PrintResult() displays the results.