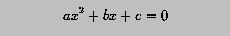
Given a quadratic equation as follows:
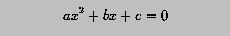
if b*b-4*a*c is non-negative, the roots of the equation can be solved with the following formulae:
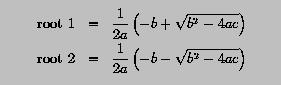
Write a program to read in the coefficients a, b and c,
and uses an internal subroutine to solve the equation. Note that a
quadratic equation has repeated root if b*b-4.0*a*c is equal to zero.
![]()
! --------------------------------------------------------------------
! PROGRAM QuadraticEquation:
! This program calls subroutine Solver() to solve quadratic
! equations.
! --------------------------------------------------------------------
PROGRAM QuadraticEquation
IMPLICIT NONE
INTEGER, PARAMETER :: NO_ROOT = 0 ! possible return types
INTEGER, PARAMETER :: REPEATED_ROOT = 1
INTEGER, PARAMETER :: DISTINCT_ROOT = 2
INTEGER :: SolutionType ! return type variable
REAL :: a, b, c ! coefficients
REAL :: r1, r2 ! roots
READ(*,*) a, b, c ! read in coefficients
CALL Solver(a, b, c, r1, r2, SolutionType) ! solve it
SELECT CASE (SolutionType) ! select a type
CASE (NO_ROOT) ! no root
WRITE(*,*) "The equation has no real root"
CASE (REPEATED_ROOT) ! repeated root
WRITE(*,*) "The equation has a repeated root ", r1
CASE (DISTINCT_ROOT) ! distinct roots
WRITE(*,*) "The equation has two roots ", r1, " and ", r2
END SELECT
CONTAINS
! --------------------------------------------------------------------
! SUBROUTINE Solver():
! This subroutine takes the coefficients of a quadratic equation
! and solve it. It returns three values as follows:
! (1) Type - if the equation has no root, a repeated root, or
! distinct roots, this formal arguments returns NO_ROOT,
! REPEATED_ROOT and DISTINCT_ROOT, respectively.
! Note that these are PARAMETERS declared in the main
! program.
! (2) Root1 and Root2 - if there is no real root, these two formal
! arguments return 0.0. If there is a repeated
! root, Root1 returns the root and Root2 is zero.
! Otherwise, both Root1 and Root2 return the roots.
! --------------------------------------------------------------------
SUBROUTINE Solver(a, b, c, Root1, Root2, Type)
IMPLICIT NONE
REAL, INTENT(IN) :: a, b, c
REAL, INTENT(OUT) :: Root1, Root2
INTEGER, INTENT(OUT) :: Type
REAL :: d ! the discriminant
Root1 = 0.0 ! set the roots to zero
Root2 = 0.0
d = b*b - 4.0*a*c ! compute the discriminant
IF (d < 0.0) THEN ! if the discriminant < 0
Type = NO_ROOT ! no root
ELSE IF (d == 0.0) THEN ! if the discriminant is 0
Type = REPEATED_ROOT ! a repeated root
Root1 = -b/(2.0*a)
ELSE ! otherwise,
Type = DISTINCT_ROOT ! two distinct roots
d = SQRT(d)
Root1 = (-b + d)/(2.0*a)
Root2 = (-b - d)/(2.0*a)
END IF
END SUBROUTINE Solver
END PROGRAM QuadraticEquation
Click here to download this program.
3.0 6.0 2.0 The equation has two roots -0.422649741 and -1.57735026
1.0 -2.0 1.0 The equation has a repeated root 1.
1.0 1.0 1.0 The equation has no real root