Studying cloud physics and chemistry is much, much easier if you can create a cloud in the lab. Claudio Mazzoleni, Lynn
Mazzoleni, Raymond Shaw and I
have developed a chamber that combines the ability to create clouds
with the capacity to generate well-characterized, reproducible
turbulence. It's called the Pi Chamber because of the internal volume
of 3.14 cubic meters with the cylindrical insert in place. (It was also
delivered to Michigan Tech on March 14, but that was just a
coincidence.)The pressure range is 1 to 0.1 atmospheres and the temperature span is +50 to -55 Celsius, which covers most of the troposphere. We can also control the temperature of the floor, ceiling and walls independently, which means we can set up conditions that give us Rayleigh-Benard convection. We've held a mixing cloud in the chamber for over 10 hours.
We have shown that aerosol-cloud interactions may help to open the bottleneck between condensational growth and runaway collision-coalescence (here and here). We've also done some work with mixed phase clouds.
The Pi Chamber page is here.
A video with a short overview of the chamber.
A video of a mixing cloud in the chamber.
First article, describing the chamber.
See Publications page for complete listing.
Heterogeneous Freezing
Water exists in the atmosphere as a vapor, liquid, and crystal (ice). The details of how water is transformed from a vapor to a liquid, and then subsequently to a solid also has important implications for weather and climate.
We can usually predict the number of liquid water cloud droplets fairly well, because we understand the basic phyiscal and chemical principles that govern the process. (If organic compounds are involved, the accuracy of the prediction may suffer because we don't know some of the properties of the compounds or the resulting solution as well as we would like.)
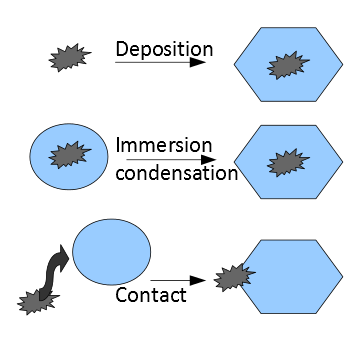In contrast, prediction of the number of ice crystals that form is much
less certain because the process (or processes) that lead to freezing
are not as well understood. The schematic to the right illustrates
various ways that a pre-exisiting aerosol particle can catalyze
freezing.One way to try to understand this process is to conduct experiments. Another is to simulate the behavior of water in contact with a surface. You would like to compare those two approaches, but it is quite difficult in many cases. Natural surfaces are complicated by the presence of atomic scale roughness, defects, and other imperfections. While those types of features can be included in simulations, you can never be sure that the imperfections that you model are actually the ones present on the surface in your experiments. Sapna Sarupria and I are attempting to overcome this difficulty by investigating the properties of water on mica. I am performing experiments while Sapna is using advanced simulation techniques to understand the structure and dynamics of water interacting with mica. Why mica? Because when you peel a sheet of mica apart you get two nearly atomically smooth surfaces. (No defects!) We think that we can reasonably compare experiments and simulations of this system.
Contact Freezing
If a particle is immersed within a droplet, the characteristic freezing temperature is typically lower than if that same particle were at the surface of the droplet. (See the last row in the schematic above.) Why is that? There are some good guesses out there, but no one has really nailed it yet. Claudio Mazzoleni and I collaborated on a project to investigate contact freezing. We have developed a technique to measure it, and have shown that for temperatures between about -15 and -22 C, contact freezing is more likely than immersion freezing for every substance we've tested (mostly mineral dusts). In collaboration with Jennifer Becker, we also tested some bacteria and found that even bacteria which are not ice positive can be effective contact freezing nuclei.
We have also shown that you can persuade water to freeze if you drop salt on it! That's surprising because salt dissolved in water will lower the freezing point. We did some prelimary tests where we cooled a droplet to -15, for example, then just dropped table salt on it. It froze! Apparently, just the impact was enough to catalyze the phase transition. We then came up with a technique to test this more systematically. We thought that maybe the freezing was because a lot of salts are endothermic upon dissolution, cooling the water. Maybe the water got cold enough for freezing to take place before the ions from the dissolved salt diffused into the volume. But then we tested NaOH. That's exothermic upon dissolution. The truth is, I told Joseph to test this one just for the sake of completeness. I knew that we wouldn't see freezing. But Joseph came back the next day and said... "It freezes." It's fun when nature surprises you. Eventually we saw that the threshhold freezing temperature correlated with the density of the salt, suggesting that it is the kinetic energy of the impact that controls freezing. We were also able to use the timescales for the propagation of a sound wave through the test droplet and the diffusion of heat and ions to place limits on the timescale in which the nucleation event takes place. Our best estimate is currently 10 nanoseconds.
Microstructure of Ice
This started because Alex Kostinski and I were talking about a class I was teaching as we walked home together. I had assigned the students in the class to calculate the entropy of liquid water at room temperature. I had given them a table of heat capacities for ice and for liquid water. When I had done the calculation, I had been a little surprised at just how linear the entropy is from about 1 Kelvin up to the melting point. As I discussed the problem with Alex, we moved on to the fact that freezing of supercooled water is irreversible (in the thermodynamic sense, of course). Does that have consequences?
It does. The latent heat of freezing is actually lower when supercooled water freezes as compared to the reversible phase transition. (Recall that the phase transition is only reversible on the phase boundary.) We predicted, based on that argument, that ice created from deeply supercooled water should have more defects than if the freezing starts from a higher temperature.