Negative Refraction Gives Rise to the Klein Paradox [Jun 1, 2009]

Negative refraction of electromagnetic waves (left) and relativistic spin-zero particles (right). The latter was generated from the former by an underlying mathematical relation.
We introduced in relativistic quantum mechanics the negative refraction phenomenon for the first time, which was previously shown only in the classical electrodynamics and acoustic domains. Our results were published in Physical Review A [1]. First experimental verification of electromagnetic negative refraction in metamaterials was achieved in 2001 in our campus (University of California, San Diego) [2]. Metamaterials potentially lead to the applications superior to conventional devices including compact antennas for mobile stations, imaging beyond the diffraction limit, and high-resolution radars, not to mention the anomalous wave propagation in fundamental optics.
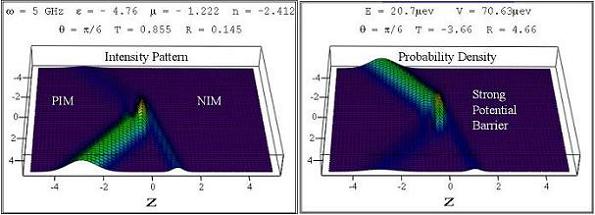
In an entirely different domain, in Phys. Rev. A we reported how the LHMs could indeed simulate the negative refraction of spin-zero particles interacting with a strong potential barrier. Hence, they give rise to the Klein paradox--a counterintuitive phenomenon in relativistic quantum mechanics.
We explained the underlying physics of the similar wave propagation behaviors in the Klein-Gordon and the Maxwellian pictures. By taking the three spatial coordinates into account [3], the generation of scalar particles in the presence of a strong Klein step potential [4-6] has been considered. We considered two-dimensional (2D) scattering from a semi-infinite Klein step potential. Hence, the negative refraction was treated explicitly in our Phys. Rev. A article first, inspired by the works about its optical counterpart, LHM [7,8-10]. It is amazing that the 2D case not only verifies the Klein paradox existing in one dimension, but it also shows the negative refraction of matter waves.
In the territory of electronics, also inspired by LHMs, negative refraction was recently predicted theoretically in a Science paper by Cheianov et al. [11] in a monolayer of graphite (graphene). Graphene not only leads to the focusing of electrons [11] similar to the perfect optical lens, but also exhibits the Klein paradox [12,13]. However, no link between the Klein paradox and the negative refraction has been found in graphene.
Our work has implications to the analog quantum simulations of many exotic phenomena in quantum electrodynamics with relatively simple optical benchtop experiments and metamaterial designs on demand.
References
[1] D. O. Guney and D. A. Meyer, Negative refraction gives rise to the Klein paradox, Phys. Rev. A 79, 063834 (2009).
[2] R. A. Shelby, D. R. Smith, S. Schultz, Experimental verification of a negative index of refraction, Science 292, 77 (2001).
[3] S. P. Kim and D. N. Page, Schwinger pair production via instantons in strong electric fields, Phys. Rev. D 65, 105002 (2002).
[4] G.-J. Ni, W. Zhou, and J. Yan, Klein paradox and antiparticle, arXiv:quant-ph/9905044.
[5] H. Nitta, T. Kudo, and H. Minowa, Motion of a wave packet in the Klein paradox, Am. J. Phys. 67, 966 (1999).
[6] A. Calogeracos and N. Dombey, Klein tunneling and the Klein paradox, Int. J. Mod. Phys. A 14, 631 (1999).
[7] V. G. Veselago, The electrodynamics of substances with simultaneously negative values of epsilon and mu, Sov. Phys. Usp. 10, 509 (1968).
[8] P. M. Valanju, R. M. Walser, and A. P. Valanju, Wave refraction in negative-index media: always positive and veery inhomogeneous, Phys. Rev. Lett. 88, 187401 (2002).
[9] D. R. Smith, D. Schurig, and J. B. Pendry, Negative refraction of modulated electromagnetic waves, Appl. Phys. Lett. 81, 2713 (2002).
[10] S. Foteinopoulou, E. N. Economou, and C. M. Soukoulis, Refraction in media with a negative refractive index, Phys. Rev. Lett. 90, 107402 (2003).
[11] V. V. Cheianov, V. Falíko, and B. L. Altshuler, The Focusing of Electron Flow and a Veselago Lens in Graphene p-n Junctions, Science 315, 1252 (2007).
[12] M. I. Katsnelson, Graphene: carbon in two dimensions, Mater. Today 10, 20 (2007).
[13] M. I. Katsnelson, K. S. Novoselov, and A. K. Geim, Chiral tunnelling and the Klein paradox in graphene, Nat. Phys. 2, 620 (2006).