Loss-Free Metamaterials without Gain Medium [Jul 17, 2015]
Metamaterials have led to previously unthought of applications such as a flat lens [1,2], perfect lens [3], hyperlens [4-7], ultimate illusion optics [8-10], perfect absorber [11,12], optical analog simulators [13,14], enhanced photovoltaics [15], and more recently in quantum information processing [16,17]. Despite tremendous progress in theory and experimental realizations, the major current challenges seem to further delay the metamaterial era to come. Perhaps the most critical challenge is how to avoid optical losses—especially in large-volume structures. The performance of devices utilizing metamaterials dramatically degrades at optical frequencies due to significant Ohmic losses arising from the metallic constituents. The strategies proposed to mitigate the losses include passive reduction and active compensation schemes. Active compensation of losses using a gain medium has emerged as the most promising strategy to avoid the deleterious impacts of losses on metamaterial devices. Although important progress has been made in theory [18-22] and experiments [18,19,23-26], the viability of active compensation of loss by gain medium is questionable [18] for practical applications such as diffraction-unlimited flat lens.
We discovered a novel optical amplification technique to compensate and control losses in metamaterials. Our results are published in Jul 17 issue of Physical Review Letters [27]. Our amplification scheme is ideally suited for compensating losses in metamaterials operating in the visible spectrum and is fundamentally different from major amplification schemes based on stimulated optical emission, Raman scattering, and optical parametric amplification. It does not require gain medium, interaction with phonons, or any nonlinear medium, and it operates at room temperature. Our technique relies on the constructive interference of externally injected SPPs within the metamaterial to coherently amplify the domestic SPPs of the metamaterial. The amplified SPPs are then coupled into the free space at the output port of the metamaterial. We have shown that this proposed scheme, referred to as the plasmon injection (PI or Π) scheme, provides loss-free optical metamaterials without using an optical gain providing medium (see Figure below).

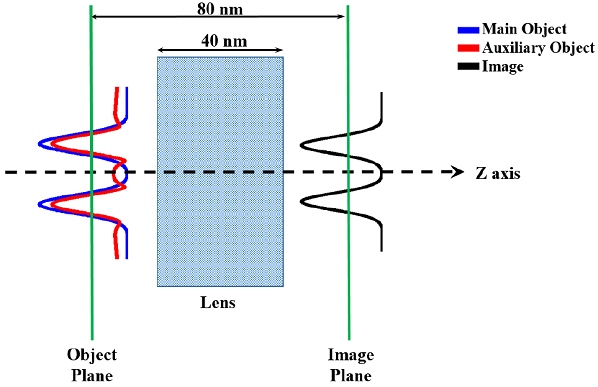
Setup for the Π scheme assisted imaging. Coherent superposition of the main object to be imaged (i.e., referred to as A in the text) and the auxiliary object (i.e., referred to as B in the text) in the object plane results in a loss compensated image in the image plane. The thickness of the lens in the present example is 40nm. The distance between the object and image planes is 80nm.
Our work received wide media coverage and picked up by NSF. See for example,
- Bringing Back the Magic in Metamaterials, Allison Mills, Michigan Tech News (Jul 21, 2015).
- “Perfect Lens” Breakthrough Could Turn Your Smartphone Into An Ultra-Powerful Microscope, Jonathan O'Callaghan, IFL Science (Jul 20, 2015)
- Scientists Get Closer to Creating the “Perfect Lens” with Metamaterials, Technology.Org (Jul 20, 2015).
- The perfect lens: Bringing back the magic in metamaterials, ScienceDaily (Jul 17, 2015).
References
[1] V. G. Veselago, Sov. Phys. Usp. 10, 509 (1968).
[2] T. Xu, A. Agrawal, M. Abashin, K. J. Chau, and H. J. Lezec, Nature 497, 470 (2013).
[3] J. B. Pendry, Phys. Rev. Lett. 85, 3966 (2000).
[4] Z. Liu, H. Lee, Y. Xiong, C. Sun, and X. Zhang, Science 315, 1686 (2007).
[5] X. Zhang and Z. Liu, Nat. Mater. 7, 435 (2008).
[6] R. Junsuk, Z. Ye, Y. Xiong, X. Yin, Z. Liu, H. Choi, G. Bartal, and X. Zhang, Nat. Commun. 1, 143 (2010).
[7] J. Sun, M. I. Shalaev, and N. M. Litchinitser, Nat. Commun. 6, 7201 (2015).
[8] J. B. Pendry, D. Schurig, and D. R. Smith, Science 312, 1780 (2006).
[9] U. Leonhardt, Science 312, 1777 (2006).
[10] D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, Science 314, 977 (2006).
[11] N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith, and W. J. Padilla, Phys. Rev. Lett. 100, 207402 (2008).
[12] K. Aydin, V. E. Ferry, R.M. Briggs, and H. A. Atwater, Nat. Commun. 2, 517 (2011).
[13] D. O. Guney and D. A. Meyer, Phys. Rev. A 79, 063834 (2009).
[14] D. A. Genov, S. Zhang, and X. Zhang, Nat. Phys. 5, 687 (2009).
[15] A. Vora, J. Gwamuri, N. Pala, A. Kulkarni, J. M. Pearce, and D. O. Guney, Sci. Rep. 4, 4901 (2014).
[16] M. A. al Farooqui, J. Breeland, M. I. Aslam, M. Sadatgol, S. K. Ozdemir, M. Tame, L. Yang, and D. O. Guney, Opt. Express 23, 17941 (2015).
[17] M. Asano, M. Bechu, M. Tame, S. K. Ozdemir, R. Ikuta, D. O. Guney, T. Yamamoto, L. Yang, M. Wegener, and N. Imoto, arXiv: 1507.07948.
[18] C. M. Soukoulis and M. Wegener, Science 330, 1633 (2010).
[19] C. M. Soukoulis and M. Wegener, Nat. Photonics 5, 523 (2011).
[20] A. Fang, T. Koschny, and C. M. Soukoulis, Phys. Rev. B 82, 121102(R) (2010).
[21] S.Wuestner, A. Pusch, K. L. Tsakmakidis, J. M. Hamm, and O. Hess, Phys. Rev. Lett. 105, 127401 (2010).
[22] A. Fang, Z. Huang, T. Koschny, and C. M. Soukoulis, Opt. Express 19, 12688 (2011).
[23] E. Plum, V. A. Fedotov, P. Kuo, D. P. Tsai, and N. I. Zheludev, Opt. Express 17, 8548 (2009).
[24] N. Meinzer, M. Ruther, S. Linden, C. M. Soukoulis, G. Khitrova, J. Hendrickson, J. D. Olitzky, H.M. Gibbs, and M. Wegener, Opt. Express 18, 24140 (2010).
[25] S. Xiao, V. P. Drachev, A. V. Kildishev, X. Ni, U. K. Chettiar, H.-K. Yuan, and V. M. Shalaev, Nature (London) 466, 735 (2010).
[26] D. Y. Fedyanin, A. V. Krasavin, A. V. Arsenin, and A. V. Zayats, Nano Lett. 12, 2459 (2012).
[27] M. Sadatgol, S. K. Ozdemir, L. Yang, and D. O. Guney, Phys. Rev. Lett. 115, 035502 (2015).