Surface Plasmon Driven Negative Index Metamaterials
Abstract: In this project we investigate the interaction of Surface Plasmon Polariton (SPP) and Localized Surface Plasmon (LSP) and develop strategies to develop low-loss metamaterials that can operate at optical frequencies. Prelimanary studies show that the interaction of the SPPs of a thin metal film and LSPs of nearby periodic nano-structures can be utilized to realize negative index metamaterials in the visible spectrum.
Keywords: Metamaterials, Plasmonics
Collaborators: Costas Soukoulis (Ames Laboratory), Thomas Koschny (Ames Laboratory), Philip Evans (Oak Ridge National Laboratory)
Support: NSF, ONR (current); DOE, AFOSR, ORAU, ORNL (past)
Metamaterials and plasmonics are two rapidly growing areas of research motivated by their potential applications relevant to defense, security, communications, computing, energy, and health. Interplay between metamaterials and surface plasmons can lead to superior applications, such as ultra-high-resolution imaging and high-precision lithography. Metamaterials are man-made, usually periodic structures, with subwavelength feature sizes. Given the capability to tailor the underlying effective electromagnetic constitutive parameters (ε and μ) of metamaterials almost arbitrarily [1], one can envision a wide range of interesting applications as varied as perfect lenses [2], invisibility cloaks [3], quantum levitation [4], compact antennas [5], and optical analog simulators [6,7]. On the other hand, plasmonic waveguides, resonators, beam splitters, and interferometers can provide high-density integration of optical circuits with broadband operation [8]. Surface plasmons, key to these miniaturized devices, are collective electronic charge oscillations residing usually at the metal-dielectric interfaces [9,10]. Surface plasmon polaritons (SPPs) are the surface modes excited by the interaction of surface plasmons with photons. Their dispersion can be controlled by metamaterial surfaces [11,12]. Surface plasmons cannot interact directly with free-space photons, owing to the momentum mismatch. Common approaches to facilitate this interaction are attenuated total reflection [13–15], which makes use of evanescent coupling of total internally reflected photons to surface plasmons, gratings, or nanostructures introduced on or in the vicinity of metal surfaces [16,17].
Surface Plasmon Driven Metamaterial Resonators
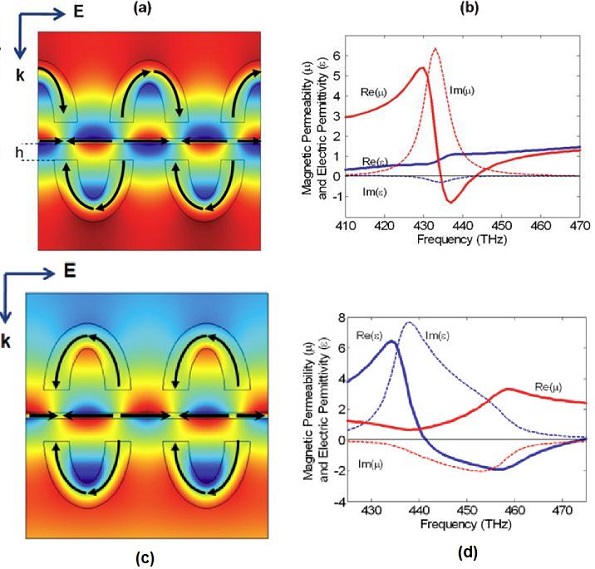
Although reducing the geometric dimensions of conventional metamaterials can lead to higher operating frequency, it cannot be scaled to arbitrarily high operating frequencies [18–20]. This is not only owing to difficulty in fabrication, but also there is a physical limit that prohibits further scaling. At substantially high frequencies the effective mass of electrons becomes important. This breaks the linear scaling and, hence, the operating frequency saturates. Our plasmonic approach in this project has opened the possibility to scale the operating frequencies to visible frequencies and beyond. It is also worth mentioning that previously proposed excitations of surface plasmons using nanostructures rely on electric coupling of the incident field [16,17]. Here, in addition to electric excitation [see Fig. 1(a) and (b)], we have also shown the magnetic excitation [see Fig. 1(c) and (d)] of surface plasmons on thin metal film. This can facilitate the designs of impedance-matched metamaterials for highly demanded applications, in particular, high-efficiency solar energy concentration, high-resolution imaging [2,21], and high-precision lithography [22].

Figure 1 Surface plasmon coupled metallic U-shaped nanostructures as a magnetic resonator. (a) Surface plot shows the magnetic-field distribution and the black arrows show the direction of currents under normal plane-wave incidence. The incident field is polarized in the horizontal direction to couple to the structure, which is translation invariant in the direction of the magnetic field. The separation between the U’s and the thin metal film is h=7.5 nm. The thickness of the thin film is 2.5 nm. The thickness of the U’s is 11 nm and is uniform along their arms. The vertical distance between the tip of the U’s and the film surface is 38 nm. The length of the unit cell along the direction of propagation is 102.76 nm. All metals are gold and described by the Drude model with the plasma frequency fp =2175 THz and the collision frequency fc =6.5 THz. The background is polyimide with the relative permittivity εr =3.5. Surface plasmon coupling to the U’s leads to a net magnetic moment. (b) Retrieved effective relative permittivity ε and permeability μ using the homogeneous effective-medium approximation. μ is negative over a bandwidth of ~9 THz. (c) Surface plasmon coupled metallic U-shaped nanostructures as an electric resonator. The separation between the U’s and the thin metal film is h=10 nm. Surface plasmon coupling to the U’s results in a net electric moment. (d) Retrieved effective ε and μ using the homogeneous effective-medium approximation. ε is negative over a bandwidth of ~32 THz.
Acknowledgments
We collaborate with Costas Soukoulis (Ames Laboratory), Thomas Koschny (Ames Laboratory), Philip Evans (Oak Ridge National Laboratory).
This project is currently funded in part by the National Science Foundation (NSF) under grant ECCS-1202443 and ONR (award N00014-15-1-2684). In the past, the project was supported by the US Department of Energy (Basic Energy Sciences) and partially by AFOSR.
References
[1] D. O. Guney, Th. Koschny,M. Kafesaki, and C.M. Soukoulis, Opt. Lett. 34, 506 (2009).
[2] J. B. Pendry, Phys. Rev. Lett. 85, 3966 (2000).
[3] D. Schurig, J. J. Mock, B. J. Justice, S. A. Cummer, J. B. Pendry, A. F. Starr, and D. R. Smith, Science 314, 977 (2006).
[4] U. Leonhardt and T. G. Philbin, New J. Phys. 9, 254 (2007).
[5] I. Bulu, H. Caglayan, K. Aydin, and E. Ozbay, New J. Phys. 7, 223 (2005).
[6] D. O. Guney and D. A. Meyer, Phys. Rev. A 79, 063834 (2009).
[7] D. A. Genov, S. Zhang, and X. Zhang, Nat. Phys. 5, 687 (2009).
[8] S. I. Bozhevolnyi, V. S. Volkov, E. Devaux, J.-Y. Laluet, and T. W. Ebbesen, Nature (London) 440, 508 (2006).
[9] R. H. Ritchie, Phys. Rev. 106, 874 (1957).
[10] E. N. Economou, Phys. Rev. 182, 539 (1969).
[11] R. Ruppin, Phys. Lett. A 277, 61 (2000).
[12] R. Ruppin, J. Phys.: Condens. Matter 13, 1811 (2001).
[13] A. Otto, Z. Phys. 216, 398 (1968).
[14] A. Otto, Z. Phys. 219, 227 (1969).
[15] B. Wang, W. Dai, A. Fang, L. Zhang, G. Tuttle, Th. Koschny, and C. M. Soukoulis, Phys. Rev. B 74, 195104 (2006).
[16] A. Ghoshal and P. G. Kik, J. Appl. Phys. 103, 113111 (2008).
[17] A. Ghoshal and P. G. Kik, Appl. Phys. Lett. 94, 251102 (2009).
[18] J. Zhou, Th. Koschny, M. Kafesaki, E. N. Economou, J. B. Pendry, and C. M. Soukoulis, Phys. Rev. Lett. 95, 223902 (2005).
[19] M. W. Klein, C. Enkrich, M. Wegener, C. M. Soukoulis, and S. Linden, Opt. Lett. 31, 1259 (2006).
[20] D. O. Guney, Th. Koschny, and C. M. Soukoulis, Phys. Rev. B 80, 125129 (2009).
[21] Th. Koschny, R. Moussa, and C. M. Soukoulis, J. Opt. Soc. Am. B 23, 485 (2006).
[22] T. Xu, Y. Zhao, J. Ma, C. Wang, J. Cui, C. Du, and X. Luo, Opt. Express 16, 13579 (2008).