Klein Paradox
Abstract: Quantum simulations is one of the main applications proposed for quantum computers. Direct simulations of, for example, an n-qubit system requires an exponential amount of space in the memory of a classical computer, which renders determining the dynamical evolution of the system intractable. Programmable 'analog' quantum computer, however, could simulate the behavior of any quantum system on demand. In this project we, particularly, explore the Klein paradox and related problems in QED and propose metamaterials as a means to simulate such systems.
Keywords: Klein Paradox, Metamaterials, Quantum Simulations
Collaborators: David A. Meyer (UC San Diego)
Support: NSA, ARDA, ARO (past)
In 1968, Veselago [1] demonstrated that the refractive index (n) of materials should be negative when permittivity (epsilon) and permeability (mu) are simultaneously negative. In his paper, Veselago called such materials left-handed materials (LHMs) and treated them purely formally, since no such materials had been discovered or created at that time. Nonetheless, he gave a number of arguments about how one should look for such materials. He pointed out that the Doppler effect, Cerenkov radiation, and even Snell's law are inverted. He also considered some questions related with the physical realization of materials with epsilon < 0 and mu < 0. His work undoubtedly raised interest in the phenomena of LHMs.
It has been demonstrated that an effective LHM, which consists of periodic array of split ring resonators (SRRs) and continuous wires manifests n < 0 for a certain frequency region in the microwave regime, which then leads to anomalous electromagnetic wave propagation [2-3].
An experimental verification of a negative index has been established by R. A. Shelby et al [4]. Subsequently, we have observed [5] that there is a situation in relativistic quantum theory that also results in similar anomalous wave propagation. The interaction of a relativistic quantum particle with a strong step potential displays a peculiar phenomenon, known as the Klein paradox. One interesting outcome of the paradox is classically forbidden transmission through strong potential barrier, where the height of the barrier is larger than the total energy of the incident particle. Furthermore, negative transmittance is compensated by the reflectance exceeding unity to conserve the probability. This is the essence of the Klein paradox. The paradox is resolved by employing the notion of particle-antiparticle pair production due to the strong potential. The antiparticles create a negative charged current moving away from the interface, while the particles are reflected and combined with the incident beam leading to a positively charged current moving towards the interface. As a result of this fact, group and phase velocities in the potential step become antiparallel, which results in negative refraction in two dimensions [5], analogous to the peculiar refraction phenomenon in LHMs.
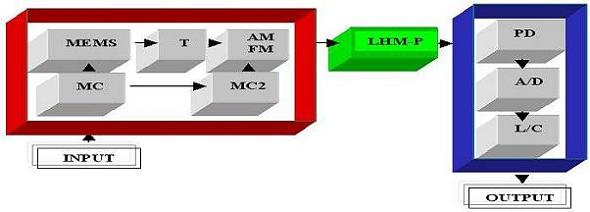
In this project we explore the analogy between LHMs and the Klein paradox mentioned above. As part of our effort we have shown that the spatial profile of the antiparticle wavefunction (or probability density) in the Klein potential could be reproduced in LHM using a TM-polarized electric field in the form of an electric field (or intensity) distribution. Figure 1 shows the block diagram of an optoelectronic simulator to emulate the Klein paradox as shown in Figure 2, where the wave propagation in the LHM is transformed into equivalent Klein problem.

Figure 1 Block diagram for the simulator. The quantum problem is defined and pre-processed in the first block and then sent to the second block. Having been solved there, it is post-processed in the third block, before obtaining output in Figure 2. The simulator mainly consists of microcontrollers (MC), microelectromechanical systems (MEMS) actuator, transmitters (T), amplitude (AM) and frequency modulators (FM), LHM, photodetectors, analog to digital converters (A/D) and logic circuits (L/C).
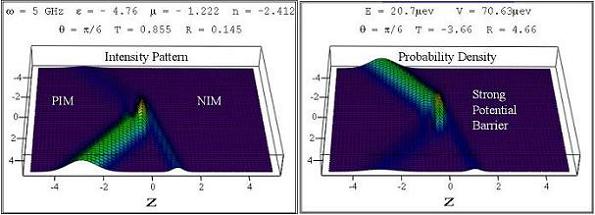
Figure 2 Simulator in Figure 1 emulates the Klein paradox by exploiting the analogous wave propagation in LHMs. It transforms the electromagnetic negative refraction (left) into negative refraction of spin-zero particles (right).
Comparing the cost for a typical high energy physics experiment with that of the optoelectronics experiment, such a processor is priceless provided that the these transformations are extended and/or shaped according to the need. In this project, we do not propose how to simulate a specific relativistic quantum field theory scenario, but rather present a proof-of-principle basic approach for using LHMs to simulate a general class of problems, some of which have (or might have) arisen in connection with the Klein paradox. This kind of simulating device, performing operations based on the mathematical connection between these two systems, could also be helpful in controlling some related quantum processes in real time, such as controlling pair production rate and distribution. Such optical devices and phenomena can be analog processors and motivating guides for the quantum world.
Our project was in part supported by the National Security Agency (NSA) and Advanced Research and Development Activity (ARDA) under Army Research Office (ARO) grant.
References
[1] V. G. Veselago, The electrodynamics of substances with simultaneously negative epsilon and mu, Sov. Phys. Usp. 10, 509 (1968).
[2] D R Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser, S. Schultz, Composite medium with simultaneously negative permeability and permittivity, Phys. Rev. Lett. 84, 4184 (2000).
[3] D. R. Smith, N. Kroll, Negative refractive index in left-handed materials, Phys. Rev. Lett. 85, 2933 (2000).
[4] R. A. Shelby, D. R. Smith, S. Schultz, Experimental verification of a negative index of refraction, Science 292, 77 (2001).
[5] D. O. Guney and D. A. Meyer, Negative refraction gives rise to Klein paradox, Phys. Rev. A 79, 063834 (2009).