Return
to Homework page | Return
to CM3110 Homepage
Homework 3
CM3110
-
Geankoplis 2.10-1 (Calculate viscosity from Hagen-Poiseuille equation).
SOLUTION
-
Using the microscopic momentum balance, calculate the velocity profile
and shear stress profile for steady Poiseuille flow in a tube. The
problem is the same as that which we solved in class using shell balances.
The solution is the same as that which we obtained using shell balances.
-
Using the microscopic momentum balance, calculate the velocity profile
and shear stress profile for steady state flow of an incompressible, power-law
fluid down an inclined plane (similar to the problem we did in class but
this time with the power-law equation instead of Newton's law of viscosity).
Use the same coordinate system as we did in class. You may assume the flow
is well developed, and you may neglect edge effects. The inclined plane
makes an angle b with gravity. SOLUTION
-
Geankoplis 3.8-8, Flow between two rotating coaxial cylinders. (Note:
the differential equation of momentum he refers to is the Navier-Stokes
equation). SOLUTION
-
In class I showed the plots of the solution for Poiseuille flow (pressure-driven
flow) in a tube of a power-law fluid. The complete solution is:
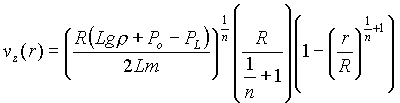 .
.
-
Non-dimensionalize this equation, i.e., cast it in the form
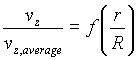 .
.
-
Using a computer (for example, Excel, Matlab, Mathematica), plot the non-dimensional
velocity function versus the non-dimensional radius for n=1, 0.8,
0.6, 0.4, and 0.2.
-
What is the effect of the power-law index, n, on the shape of the
non-dimensional velocity?
-
What is the solution for vz(r) when n=0?
SOLUTION
-
Geankoplis 2.5-1 (Calculate Reynolds number for flow of milk in a pipe).
SOLUTION
-
HONORS Problem: The equations of motion (components of the vector differential
momentum balance equation) in terms of stresses (txy,
txx,
txz,
etc.) are useful in dimensional analysis of the behavior of non-Newtonian
fluids. Show for the power-law, non-Newtonian fluid that the dimensionless
groups obtained by writing the equations of motion in dimensionless form
are
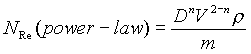 and
and 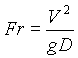 .
.
SOLUTION
Return
to Homework page | Return
to CM3110 Homepage
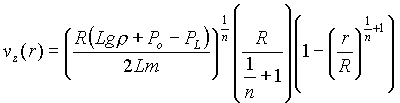 .
.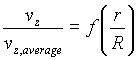 .
.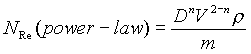 and
and 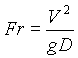 .
.