Return
to Homework page | Return
to CM3110 Homepage
Homework 3
CM3110 Transport Processes I
Dr. F. A. Morrison
- Geankoplis 3rd edition 2.10-1. Viscosity may be determined
for a
liquid by subjecting it to Poiseuille flow in a tube. In a
horizontal tube of
length 0.1585m and of diameter 2.222mm a fluid is made to flow under a
pressure drop of 131 mm water. The flow rate under these
conditions
at steady state is 5.33 X 10-7 m3/s. The
density
of the fluid is 912 kg/m3 and the density of water is 996
kg/m3.
Calculate the viscosity of the fluid; give your answer in Pa s. SOLUTION
- Using the microscopic momentum balance, calculate the velocity
profile
and shear stress profile for steady Poiseuille flow in a tube.
The
problem is the same as that which we solved in class using shell
balances.
The solution is the same as that which we obtained using shell balances.
- Using the microscopic momentum balance, calculate the velocity
profile
and shear stress profile for steady state flow of an incompressible,
power-law
fluid down an inclined plane (similar to the problem we did in class
but
this time with the power-law equation instead of Newton's law of
viscosity).
Use the same coordinate system as we did in class. You may assume the
flow
is well developed, and you may neglect edge effects. The inclined plane
makes an angle b with gravity. SOLUTION
- Calculate the steady state velocity profile and shear stress
profile
for
the flow of an incompressible, Newtonian fluid between two concentric
cylinders
when both cylinders are rotating. The radius of the inner
cylinder
is R1, and it is moving with an angular velocity of w1.
The radius of the outer cylinder is R2, and it is moving
with
an angular velocity of w2.
The cylinders are long, and we can therefore neglect the effects of the
open top and of the bottom on the flow. SOLUTION
- In class I showed the plots of the solution for Poiseuille flow
(pressure-driven
flow) in a tube of a power-law fluid. The complete solution is:
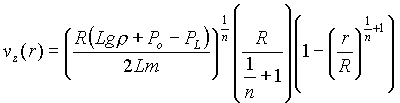 .
.
- Non-dimensionalize this equation, i.e., cast it in the
form
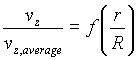 .
.
- Using a computer (for example, Excel, Matlab, Mathematica),
plot the
non-dimensional
velocity function versus the non-dimensional radius for n=1,
0.8,
0.6, 0.4, and 0.2.
- What is the effect of the power-law index, n, on the
shape of
the
non-dimensional velocity?
- What is the solution for vz(r) when n=0?
SOLUTION
- Geankoplis 3rd edition 2.5-1 Whole milk at 293K having a density
of
1030
kg/m3 and viscosity of 2.12 cp is flowing at the rate of
0.605
kg/s in a glass pipe having a diameter of 63.5 mm. a) What
is the Re number for this flow? Is the flow laminar or
turbulent?
b) Calculate the flow rate and average velocity needed for a
Reynolds
number of 2100. SOLUTION
- HONORS Problem: The equations of motion (components of the vector
differential
momentum balance equation) in terms of stresses (txy,
txx, txz,
etc.) are useful in dimensional analysis of the behavior of
non-Newtonian
fluids. Show for the power-law, non-Newtonian fluid that the
dimensionless
groups obtained by writing the equations of motion in dimensionless
form
are
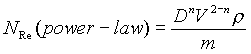 and
and 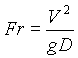 .
.
SOLUTION
Return
to Homework page | Return
to CM3110 Homepage
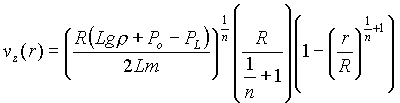 .
.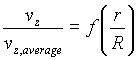 .
.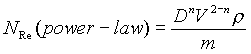 and
and 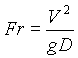 .
.