Homework 6
CM3110
-
Geankoplis 4.1-1, page 317 (Calculate the heat flux through the walls of
a cold room). SOLUTION
-
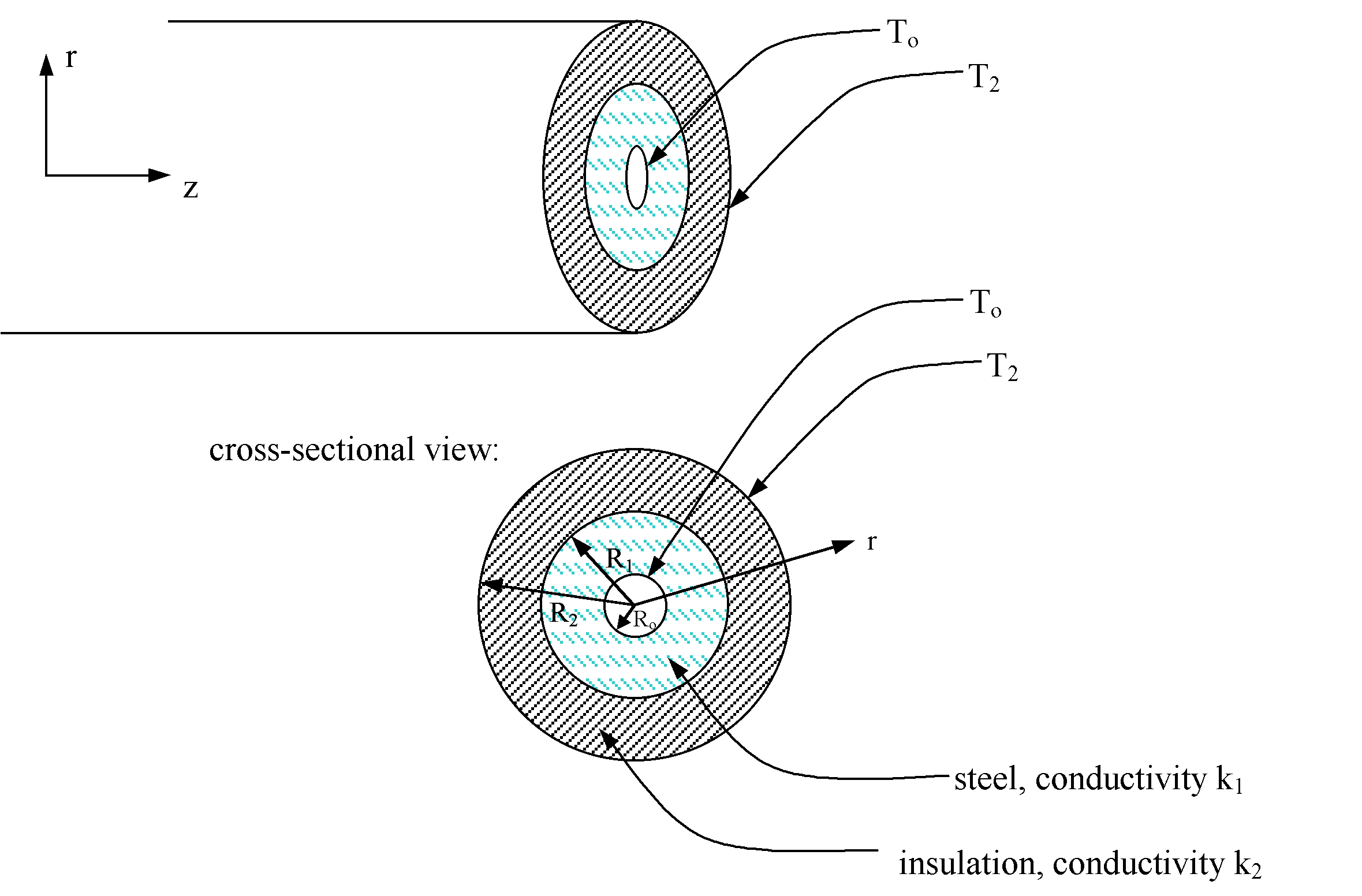
The inside wall of an insulated pipe is held at To and the surface
on the outside wall of the insulation is held at T2, where To
>
T2 (see below). Assuming that the pipe is very long and that
there is no heat loss out the ends of the pipe, calculate the steady state
temperature profile in the radial direction. Hint: within each material,
solve for T(r) the same way as we did in class. To solve for the unknown
temperature, match the solutions at the boundaries, i.e. heat flux is the
same in both materials at r = R1. SOLUTION
-
Geankoplis 4.2-1 (In radial heat flux in a pipe, if the thermal conductivity
varies linearly with temperature, show that the result for heat flux is
the same as the result obtained for constant thermal conductivity if the
value of conductivity used is the average of the values obtained at the
boundaries, km = 0.5(k(T1)+k(T2).). SOLUTION
-
Geankoplis 4.2-2 (An example of the result in problem 4.2-1 above, using
numbers). SOLUTION
-
Geankoplis 4.3-2 (Design question: calculate the thickness of insulation
given a maximum heat flux). SOLUTION
-
Geankoplis 4.3-6 (Calculate heat flux from a window/wall using heat-transfer-coefficient
boundary conditions, i.e. Newton's law of cooling). SOLUTION

