Faith A. Morrison
CM3110 notes
Fall 1998, modified September 24, 1999 and February 5, 2001
For some problems we do not need the velocity profile or information about the details of the flow to get the information we need. For these problems we do macroscopic balances, rather than the previous microscopic balances (Navier-Stokes, continuity equation).
There are three types of macroscopic balances: mass, momentum, and energy. In this handout, I discuss the macroscopic mass and momentum balances. There is a handout available on the web that discusses energy balances of all types (see http://www.chem.mtu.edu/~fmorriso/cm310/e_balance.html or energy.ps).
Macroscopic mass balance
The macroscopic mass balance is simple and perhaps obvious:
(net flow out) = (rate of depletion) (1)
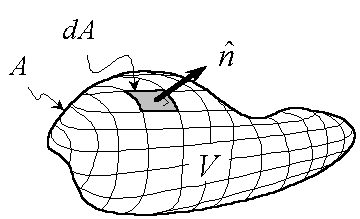
The thing to notice is that since velocity, v, and density, r, are functions of position inside the flow (e.g. velocity depends on radius), when written on the usual microscopic volume (shown below), the word-equation above becomes

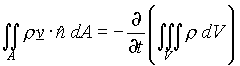 (2)
(2)
where A is the total area bounding control volume V, ![]() is
the outwardly pointing unit normal vector associated with piece of
surface
element dA, r is density and is a
function
of position, v is the velocity vector which is a
function
of position, t is time, and dV is a differential volume
element.
The left-hand side gives the net outflow of mass through the area A,
while the right-hand side gives the rate of change of mass in the
volume
V.
The negative sign on the right-hand side turns the expression into the
rate of depletion (instead of the rate of increase) of mass.
is
the outwardly pointing unit normal vector associated with piece of
surface
element dA, r is density and is a
function
of position, v is the velocity vector which is a
function
of position, t is time, and dV is a differential volume
element.
The left-hand side gives the net outflow of mass through the area A,
while the right-hand side gives the rate of change of mass in the
volume
V.
The negative sign on the right-hand side turns the expression into the
rate of depletion (instead of the rate of increase) of mass.
On the left-hand side, the different terms inside the integral combine to give,
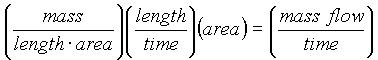 (3)
(3)
where the length/time of interest is the magnitude of the velocity
that
transports material out of the volume V. The vector velocity, v,
however, is not necessarily perpendicular to the surface, dA,
and
it is only the component of the velocity that is perpendicular to
the
surface dA that results in material being transported out of V.
The component of the velocity that is parallel to the surface dA
only carries material parallel to the surface. The component of v
perpendicular to the surface dA is given by ![]() (see
figure below).
(see
figure below).
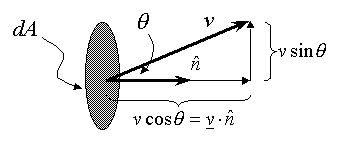
When the density is constant across the surface dA it can be
removed to the outside of the integrals in equation (2). Also, when v
is perpendicular to dA, ![]() (cos(0)
=1; cos(p)=-1). Finally, at steady
state,
the right-hand side of equation (2) becomes zero.
(cos(0)
=1; cos(p)=-1). Finally, at steady
state,
the right-hand side of equation (2) becomes zero.
A common case is when there is one inflow area, one outflow area, density is constant, and v is perpendicular to dA at both the inflow and the outflow areas. This case is shown below:
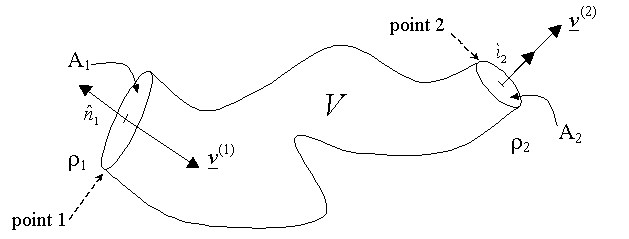
where v(1) is the vector velocity at surface A1 and v(2) is the vector velocity at surface A2.
For the case shown above at steady-state, where flow in occurs across a surface A1 and flow out occurs across a surface A2 (for example upstream and downstream positions of a pipe), the macroscopic balance in equation (2) becomes,
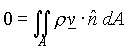 (4)
(4)
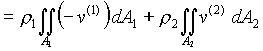 (5)
(5)
where v(1) is the magnitude of the velocity at surface 1, and v(2) is the magnitude of the velocity at surface 2. From calculus we know that the definition of the average of a two-dimensional function, f, is given by (see web page http://www.chem.mtu.edu/~fmorriso/cm310/FAQ1_page1.html for details on this):
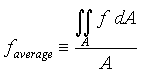 (6)
(6)
Therefore, the average values of v(1) and v(2), ![]() and
and ![]() ,
are given by
,
are given by
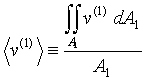 (7)
(7)
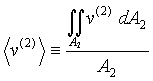 (8)
(8)
and the macroscopic mass balance of equation (5) becomes,
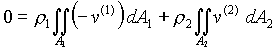 (9)
(9)
![]() (10)
(10)
which is the same as saying mass flow in equals mass flow out.
This simple equation is what we would have written down as step one under most circumstances. The purpose of showing this formal derivation is to highlight the assumptions made:
Assumptions:
Macroscopic momentum balance
The momentum balance on an arbitrary volume in a flowing fluid is
 (11)
(11)
Writing these terms in mathematical form, we get the momentum version of equation (2):
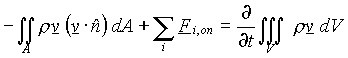 (12)
(12)
where Fi,on are all the forces acting on the fluid in volume V, and all other symbols were defined previously. Recall that the momentum balance gives a vector equation, and each term of equation (12) is a vector.
We will now write ![]() ,
where v is the magnitude of v, and define the
unit
vector
,
where v is the magnitude of v, and define the
unit
vector ![]() as the unit
vector
in the direction of v,
as the unit
vector
in the direction of v, ![]() .
With these changes, equation (12) becomes
.
With these changes, equation (12) becomes
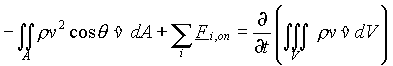 (13)
(13)
If we now make some of the same assumptions as were made in the derivation of the macroscopic mass balance, i.e.
Assumptions:
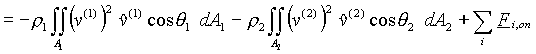 (15)
(15)
If the unit vectors ![]() and
and ![]() are
assumed not to vary over surfaces A1 and A2
respectively, then the cosq terms
and
the unit vectors themselves can come out of the integrals. What remains
in the integrals can be related to the average of the squares of the
velocities
over the two surfaces:
are
assumed not to vary over surfaces A1 and A2
respectively, then the cosq terms
and
the unit vectors themselves can come out of the integrals. What remains
in the integrals can be related to the average of the squares of the
velocities
over the two surfaces:
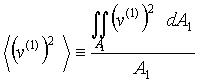 (16)
(16)
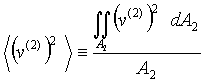 (17)
(17)
Substituting these definitions into equation (15), we obtain,
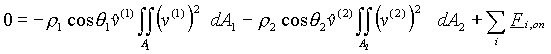 (18)
(18)
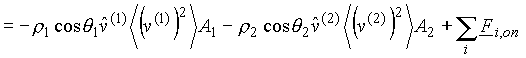 (19)
(19)
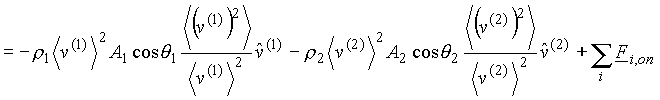 (20)
(20)
If we define m as the mass flow rate, then ![]() and
and ![]() .
The parameter b is defined for any velocity
magnitude v as
.
The parameter b is defined for any velocity
magnitude v as
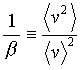 (21)
(21)
Thus, equation (20) becomes,
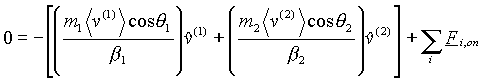 (22)
(22)
Note that this is still a vector equation. We can write three scalar
equations from this, one each for the x-, y-, and z-components.