CM3110 Fall 2006 Dr. Faith Morrison

October 26, 2006

1. When we wish to solve for a velocity profile in a flow, what balances will we employ?
2. Why are there three components to the microscopic momentum balance?
3. When we choose a control volume for performing a microscopic balance, which direction(s) must be chosen to be small, i.e. of differential length?
4. When we write the stress as t₂₁, what is the direction of the flux? what is the direction of the momentum?
5. Indicate the direction of the flux of momentum on the following drawings (the direction of the flux, not the direction of the momentum):

 
 
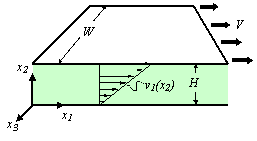
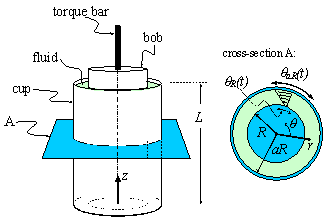
11. What is a Venturi meter?  What is an orifice meter?
12. What is Reynolds number? Where does it come from
13. What is Fanning friction factor? Where did we derive it from?
14. What is the frictional loss as a function of flow rate, Q, in a piping system that has 21 ft of straight pipe, two 90^o elbows and a gate valve?

23. What is the pressure at the bottom of each of the tanks shown above? Write your answer in terms of the variables and values given.
24. Referring to the figure below, derive an equation that relates P₁ to the variables listed for the manometer shown. Also, is r_A larger or smaller than r_f? How do you know?

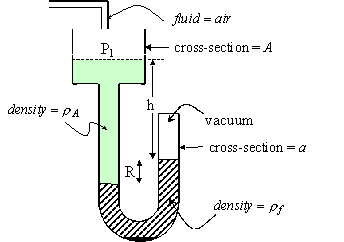
25. What is the point of designing a manometer to have a large well on one or both sides? (see figure above in last problem)
26. Calculate the velocity profile for the laminar flow of two layers of Newtonian fluid (see figure below). The bottom fluid has viscosity m₁, and the top fluid has viscosity m₂; both fluids are incompressible, and the flow is at steady state. The flow is driven by the motion of the top wall which moves at velocity V.

27. What is shear rate?
28. How is the viscosity different for a Newtonian fluid and a non-Newtonian fluid?
29. Does Newton's Law of Viscosity apply to a non-Newtonian fluid?
30. What is a power-law fluid? What is a Bingham plastic or Bingham fluid?
31. Calculate the velocity profile for the flow of a power-law, generalized Newtonian fluid down an inclined plane. The geometry and flow conditions are the same as the example we did in class except that the fluid is not Newtonian but rather is a power-law, non-Newtonian fluid.
32. Give an example of a non-Newtonian fluid.
33. You have a Newtonian fluid and a non-Newtonian fluid that have the same viscosities at low shear rates. Which will be easier to stir at high rates? Why?
34. What is yield stress?
35. What are the units of viscosity?
36. What is the defining equation of viscosity?
37. What is the vector force on a vertical wall when a jet of water flowing at 25m/s impinges on the wall? Assume that the stream splits in two streams that follow the wall, one going up and the other going down.
38. The mechanical energy balance is given below. What type of energy is associated with each term of the mechanical energy balance?




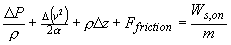
39. What type of momentum transfer is associated with each term of the macroscopic momentum balance?
40. Why is the macroscopic momentum balance a vector equation? Why is the mechanical energy balance a scalar equation?
41. What is a vector? What is a scalar?
42. What is a coordinate system?
43. The Navier-Stokes (microscopic momentum balance for Newtonian fluids) equation has three components. What balance does each of the components of the Navier-Stokes equation represent individually?
44. The equation of motion was given to you in two different forms (think of the handout with the components of the equation of motion). When would you use the version with stresses in it (on the front of the handout) and when would you use the Navier-Stokes version (on the back of the handout)?
45. What is the equation of continuity? What balance does it represent?
46. I want to calculate the force on a 70^o elbow when fluid is flowing in it. What balance will I need to apply?
47. What is the meaning of the parameter alpha that appears in the mechanical energy balance?
48. What is the meaning of the parameter beta that appears in the macroscopic momentum balance?

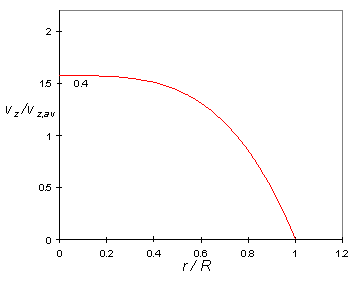
50. For pressure-driven flow in a tube (Poiseuille flow), the velocity profile of a fluid is observed to be as shown in the figure above. Is the fluid Newtonian or non-Newtonian?
51. What is an open system? What is a closed system?
52. What is stress? What is momentum flux? How are they related?
53. What is the point of non-dimensionalization?
54. What is scale-up?
55. Where does the mechanical energy balance come from?
56. What is the difference between the microscopic momentum balances and the macroscopic momentum balance?
57. What is Froude number? Where does it come from?
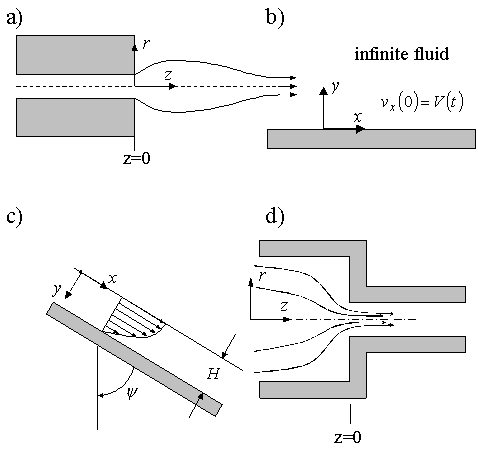
58. Write down the boundary conditions for the following flows:
59. If a sphere falls at a terminal velocity of 0.001m/s in water at room temperature, what is the drag force on the sphere?
60. The pressure drop across a packed bed of void fraction 0.45 is 12 psi.  The bed is 1m long.  What is the flow rate in the bed?
61. What is the Ergun equation?
62. An oil flows in a pipe of diameter 1" at 1 gal/min.  What is the pressure drop across the pipe?
63. Two pipes are connected in series.  The first is 1" in diameter and 40ft long, and the second is 0.5 " in diameter and 100ft long.  The upstream pressure is 60psig.  What is the flow rate through the device? (requires iteration)
    
64. What is void fraction?
65. If the velocity field in a flow of a power-law fluid is v_1=65 x_2 mm/s, v_2=0, v3_0, what is the shear stress in this flow?  You may leave the parameters m and n in your final answer.
66. What is form drag?  (flow on a sphere)
67. Calculate the velocity profile for steady pressure-driven flow of an incompressible power-law fluid in a tube.
68. Calculate the velocity profile for steady pressure-driven flow of an incompressible power-law fluid in a wide slit.
69. Calculate the velocity profile for steady pressure-driven flow of an incompressible Newtonian fluid in a slit.
70. Calculate the velocity profile for steady pressure-driven flow of an incompressible Newtonian fluid in a slit that is tilted 45 degrees upward.
71. Calculate the velocity profile for steady gravity-driven flow of an incompressible Newtonian fluid in a slit, i.e. the slit points downward.