February 15, 1999

If you have a nonlinear model with adjustable parameters and some data you would like to fit the model to, the Excel^® Solver option is a very nice way to carry out the fit. I would like to thank Michael Hickner MTU'99 for showing me how to do this.

As an example, consider the Carreau-Yasuda model for viscosity of a non-Newtonian fluid:

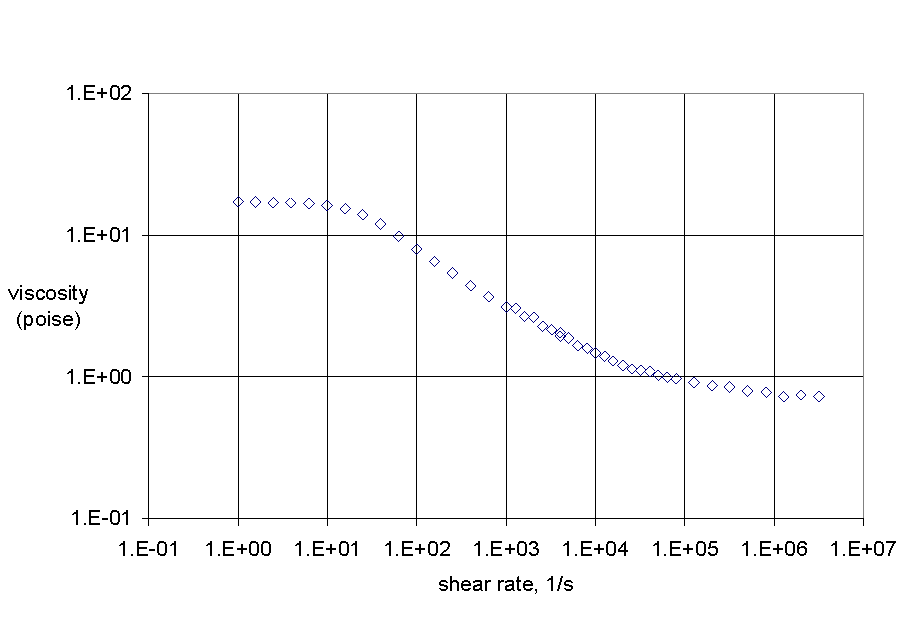
This model has 5 adjustable parameters, a, l, n, h_o, and . We would like to fit this model to some data of viscosity (h) as a function of shear rate (). Some trial data are given below and are plotted in Figure 1.

Figure 1: Plot of the example data given above for viscosity as a function of shear rate.

We begin by arranging the data in an Excel^® spreadsheet. We will use two columns, one for shear rate and one for viscosity. We now need to create a column that has a predicted value of viscosity calculated from the model above. We will put the five parameters into the spreadsheet and enter the formula for the model by referencing to the cells containing the model parameters. In our example, we will put the four parameters into cells F1 through F5. Since we do not know the values of any of our parameters, we will start with some guesses; I find that for some problems the guesses have to be pretty good ones.

Our Excel spreadsheet now looks like this:

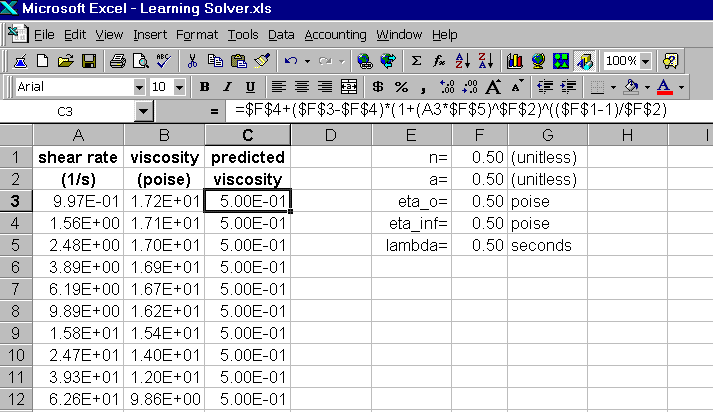
The Solver function in Excel^® is set up to minimize or maximize a cell in a spreadsheet. We will have Solver minimize the sum of the squares of the deviations between the actual viscosity data and the predicted values of viscosity. We create a column called Error that contains the differences between columns C and B, squared. Now we add up all the values in the Error column (column D) and put that value in cell F9.

To invoke Solver, we go to the Tools pull-down menu and choose Solver. The Solver dialog box asks for the following information:

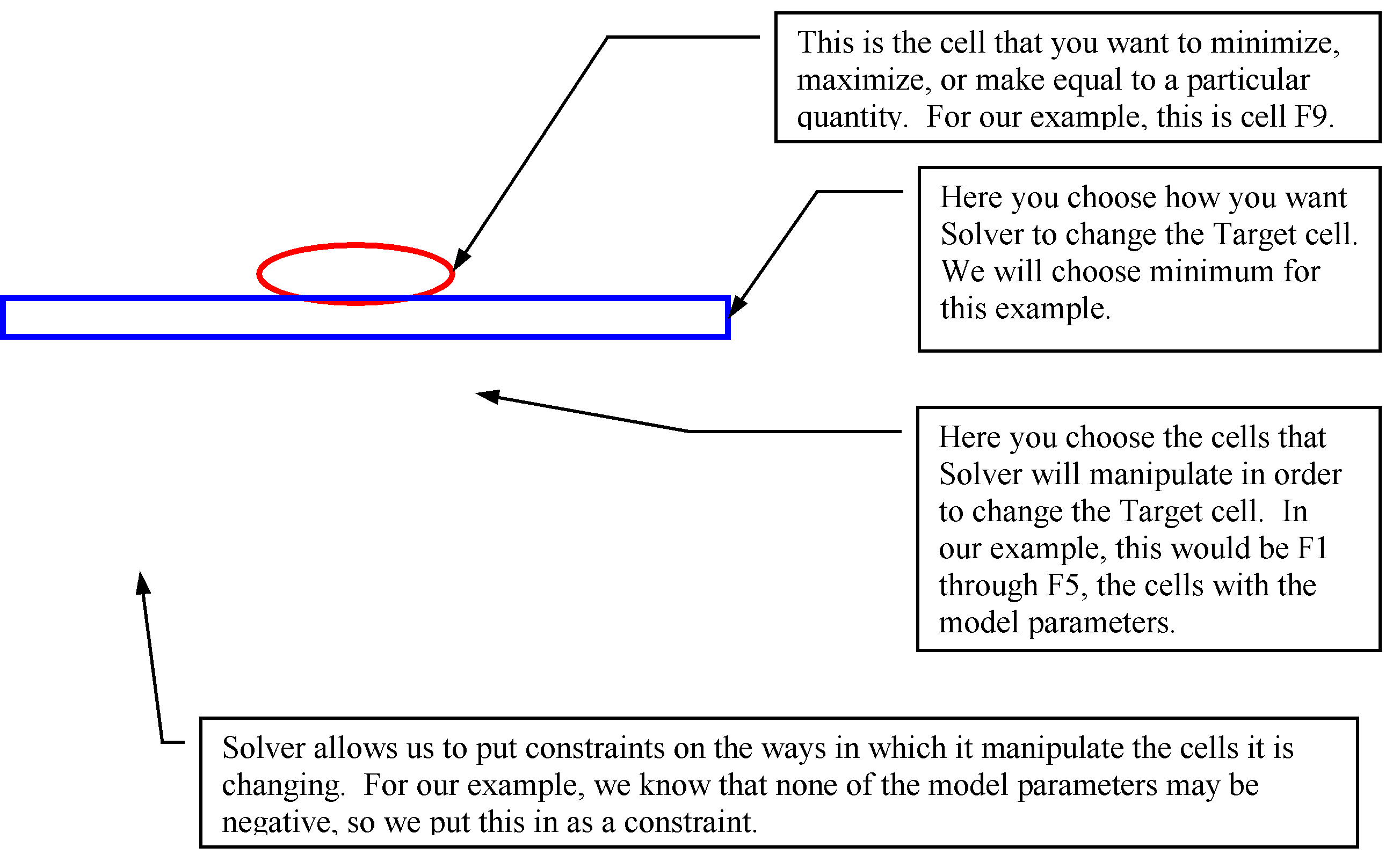
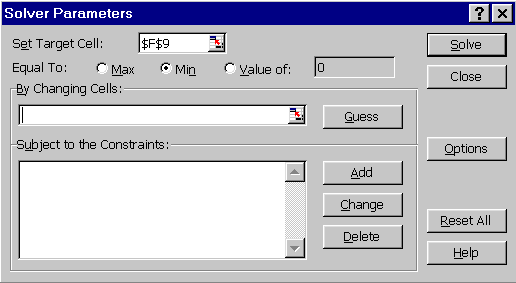
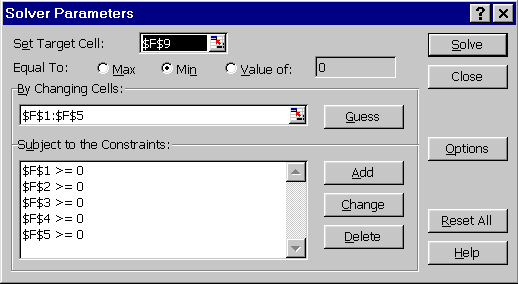
When we have finished inputting the choices for our example problem, the Solver box looks as follows:

Before solving, we need to consider the criteria that Solver will use to know when the solution is good enough. These parameters are accessible by choosing the Options button in the Solver window. The default tolerance is rather mild (5%), and I suggest you change this or run Solver more than once.

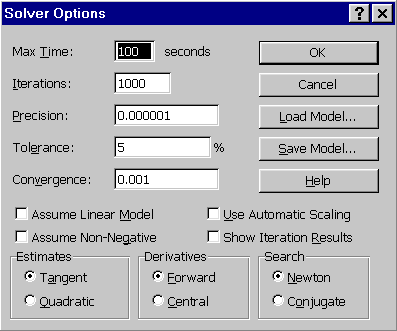
Once the Solver options are set to your satisfaction (we will change the tolerance to 0.1% and the convergence to 0.0001), click OK. To solve, we click on the button in the main Solver window. If the search is successful, the spreadsheet will appear as follows:

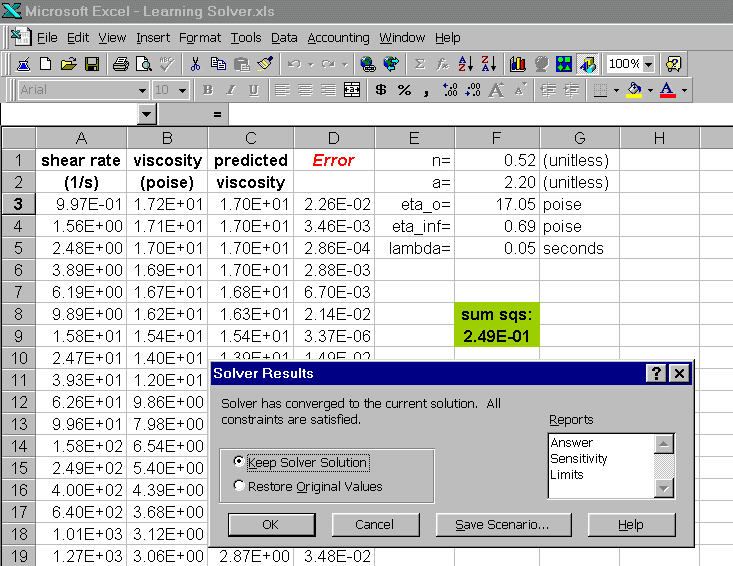
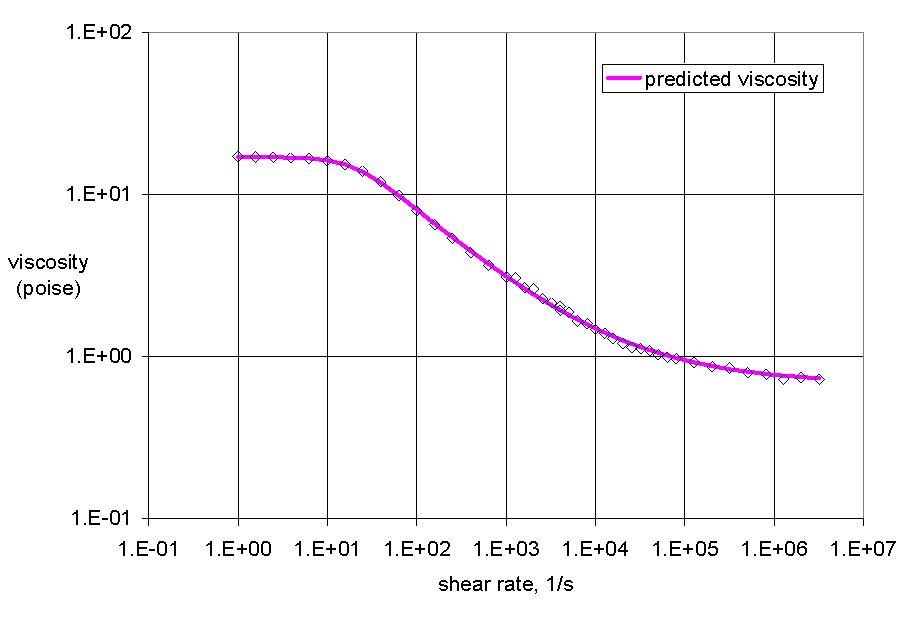
Solver has replaced our initial guesses with optimized values (see cells F1 through F5), and the dialog box gives us the option of saving that solution or restoring the original values. To check if the solution is the best possible, you can keep the solver solution and run solver again; this will run another minimization using the values from the last search as the guesses for the new search. If the optimized parameters do not change, you have arrived at the best answers. For our example, we can check the goodness-of-fit by plotting the predicted viscosity with the data. The plot below shows that the fit is very good.

Figure 2: Comparison of the model fit to the experimental data for the example given in the text.

More in-depth information about Solver can be found by trying out the various buttons or by consulting the help menu in Excel^®.