Project 3 - Logic

Food is good AND ghosts are bad,
Spock would be so proud
Introduction
In this project, you will use/write simple Python functions that generate logical sentences describing Pacman physics, aka pacphysics, and the game Clue. You will use a SAT solver, pycosat, to solve the logical inference tasks associated with planning (generating action sequences to reach goal locations) and playing Clue.
As in previous programming assignments, this assignment includes an autograder for you to grade your answers on your machine. This can be run with the command:
python autograder.py The code for this project consists of several Python files, some of which you will need to read and understand in order to complete the assignment, and some of which you can ignore. You can download all the code and supporting files as a zip archive:logic.zip.
| Files you’ll edit | |
logicPlan.py |
Where you will put your code for the various logical agents (Q1-4). |
liars.py |
Where you will put your code for the Liars logic question (Q5). |
cluedo.py |
Where you will put your code for the Clue logic questions (Q6-10). |
| Files you might want to look at | |
logic.py |
Propsitional logic code originally from https://code.google.com/p/aima-python/ with modifications for our project. There are several useful utility functions for working with logic in here. |
logicAgents.py |
The file that defines in logical planning form the two specific problems that Pacman will encounter in this project. |
pycosat_test.py |
Quick test main function that checks that the pycosat module is installed correctly. |
cluedo_game.py |
Implements running the cluedo game. Has helper functions such as printNotepad that may be helpful in your debugging. |
game.py |
The internal simulator code for the Pacman world. The only thing you might want to look at in here is the Grid class. |
cnf.py |
Tests for satisfiability with the pycosat SAT solver. |
| Files you can ignore: | |
pacman.py |
The main that runs Pacman games. |
logic_util.py |
Utility functions for logic.py |
util.py |
Utility functions primarily for other projects. |
autograder.pygrading.pyprojectParams.pylogicTestClasses.pysubmission_autograder.pytest_cases/testClasses.pytestParser.py |
Files related to autograder infrastructure for Project 2: test and solution files, test classes, parse autograder test and solution files, etc. |
graphicsDisplay.pygraphicsUtils.pytextDisplay.py |
Graphics for Pacman, Support for Pacman graphics, ASCII graphics for Pacman |
ghostAgents.py |
Agents to control ghosts |
keyboardAgents.py |
Keyboard interfaces to control Pacman |
layout.pylayouts/ |
Code for reading layout files and storing their contents |
agents.py |
Classes on general pacman agents |
Files to Edit: You will fill in portions of logicPlan.py, liars.py and cluedo.pyduring the assignment. Please do not change the other files in this distribution or submit any of our original files other than this file.
Evaluation: Your code will be autograded for technical correctness. Please do not change the names of any provided functions or classes within the code, or you will wreak havoc on the autograder. However, the correctness of your implementation – not the autograder’s judgements – will be the final judge of your score. If necessary, I will review and grade assignments individually to ensure that you receive due credit for your work.
Academic Dishonesty: I will be checking your code against other submissions in the class for logical redundancy. If you copy someone else’s code and submit it with minor changes, I will know. The code to detect this is extremely hard to fool, so please don’t try. I trust you all to submit your own work only; please don’t let me down. If you do copy someone else’s code, I will pursue the strongest consequences available to me – see the syllabus.
Getting Help: You are not alone! If you find yourself stuck on something, contact Dr. Brown for help. Office hours, and the discussion forum are there for your support; please use them. If you can’t make my office hours, let me know and I will schedule more. These projects should be rewarding and instructional, not frustrating and demoralizing.
Discussion: Please post to the discussion post about general questions, for all the class to see (and help in answering). Specific or detailed questions about your solution, can be posted privately to the instructional staff.
Propositional Logic
In this section, we give a brief overview of propositional logic (a.k.a. Boolean logic and sentential logic). For a more complete introduction, see Chapter 7 of your textbook and lecture materials.
Propositional logic is a simple logic based upon the Boolean values true and false. Many programmers will find propositional logic intuitive from exposure to Boolean types and logical operators which occur frequently in programming.
In discussing a logic, one needs to address both the syntax (structure) and the semantics (meaning) of the language. Just as the syntax of a programming language defines rules for what constitutes a well-formed program, the syntax of a logical language defines rules for what constitutes a well-formed sentence of the logic. Just as programming language specifications help the programmer understand the expected behavior of a program, the semantics of a logical language define the meaning of well-formed sentences of the logic. We will present the syntax and semantics of propositional logic one simple piece at a time.
The atomic sentence is the simplest fundamental unit of the language. The syntax of an atomic sentence is either the constant true, the constant false, or a symbol. Each symbol is associated with a statement which can be true or false. For example, $pi_{wh}$ may symbolize the statement that “The Mrs. White player is holding the Lead Pipe card.” This statement may be true or false. In general, $c_p$ will symbolize the statement “The card $c$ is in place $p$.”
Often, the symbols used for atomic sentences are capital alphabetic characters $A$,$B$,$C$,…,$Z$, but we are free to choose whichever symbols are convenient. However, just as with commenting variables in a program, it is important to attach meanings to these symbols to ground them in the reality they represent.
Example Problem: Suppose that liars always speak what is false, and truth-tellers always speak what is true. Further suppose that Amy, Bob, and Cal are each either a liar or truth-teller. Amy says, “Bob is a liar.” Bob says, “Cal is a liar.” Cal says, “Amy and Bob are liars.” Which, if any, of these people are truth-tellers?
The atomic sentences for this problem are as follows:
- $A$ - Amy is a truth-teller
- $B$ - Bob is a truth-teller
- $C$ - Cal is a truth-teller
Negation ($\neg$, “not”): More complex sentences may be built from these. The negation of $A$, denoted $\neg A$ (read “not” $A$), means the opposite of $A$, and thus means “Amy is not a truth-teller.” Given our constraint that Amy is either a truth-teller or liar, this also means “Amy is a liar.” The negation operator $\neg$ operates on a single sentence, negating its meaning. Thus for propositional logic sentence $S$, $\neg S$ has the opposite truth value. We may thus express the semantics of $\neg$ in a truth table:
| $s$ | $\neg s$ |
|---|---|
| false | true |
| true | false |
A literal is an atomic sentence or its negation. For example, $A$, $\neg A$, $B$, $\neg B$, $C$, and $\neg C$ are all literals.
Conjunction ($\wedge$ “and”): We have seen how “Amy is a liar.” can be represented as $\neg A$. Similarly, “Bob is a liar.” can be represented as $\neg B$. To say “Amy and Bob are liars.” is to say that both $\neg A$ and $\neg B$ are true. We denote this conjunction of sentences as $\neg A \wedge \neg B$ (read “not A and not B”). If either or both of the two subsentences $\neg A$ or $\neg B$ are false, then the conjunction is false as well. The semantics of $\wedge$ for sentences $S_1$ and $S_2$ are thus expressed in this truth table:
| $S_1$ | $S_2$ | $S_1 \wedge S_2$ |
|---|---|---|
| false | false | false |
| false | true | false |
| true | false | false |
| true | true | true |
Disjunction ($\vee$ “or”): Suppose that you are playing Miss Scarlett and Mrs. White suggests that Colonel Mustard committed the murder with the knife in the hall. Mr. Green refutes this suggestion by privately showing one of the cards Mustard, Knife, or Hall privately to Mrs. White. You hold the Mustard card. Thus you know that Mr. Green has either the Knife card or the Hall card. We may represent this knowledge as the disjunction $kn_{gr} \vee ha_{gr}$ (read ‘‘$kn_{gr}$ or $ha_{gr}$’’). If either or both of the two subsentences $\neg A$ or $\neg B$ are true, then the disjunction is true as well. The semantics of $\vee$ for sentences $S_1$ and $S_2$ are thus expressed in this truth table:
| $S_1$ | $S_2$ | $S_1 \vee S_2$ |
|---|---|---|
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | true |
Conditional ($\Rightarrow$ “implies”): In our truth-teller and liar example, Amy says “Bob is a liar.”. If Amy is a truth-teller ($A$), then we know that Bob is a liar ($\neg B$). We may represent this knowledge as the conditional (a.k.a. implication) $A \Rightarrow \neg B$ (read “A implies not B”). If the first subsentence $S_1$, the antecedent, is true, and the second subsentence $S_2$, the consequent, is false, then the conditional is false. Otherwise, it is true. The semantics of $\Rightarrow$ for sentences $S_1$ and $S_2$ are thus expressed in this truth table:
| $S_1$ | $S_2$ | $S_1 \Rightarrow S_2$ |
|---|---|---|
| false | false | true |
| false | true | true |
| true | false | false |
| true | true | true |
Biconditional ($\Leftrightarrow$ “if and only if”): In the previous example, $A \Rightarrow \neg B$ is not the only fact we represent from Amy saying that Bob is a liar. We also know that if we find that Bob is, in fact, a liar, then Amy must be a truth-teller. That is $\neg B \Rightarrow A$. Combining these facts in a conjunction, we fully represent the knowledge as ($A \Rightarrow \neg B$) $\wedge$ ($\neg B \Rightarrow A$). This conjunction of two conditionals with antecedents and consequents reversed has a more compact representation as the biconditional $A \Leftrightarrow \neg B$. If the first subsentence $S_1$ and the second subsentence $S_2$ have the same truth value, the biconditional is true. Otherwise, it is false. The semantics of $\Leftrightarrow$ for sentences $S_1$ and $S_2$ are thus expressed in this truth table:
| $S_1$ | $S_2$ | $S_1 \Leftrightarrow S_2$ |
|---|---|---|
| false | false | true |
| false | true | false |
| true | false | false |
| true | true | true |
As with arithmetic expressions, there is an order of precedence of the operators. The negation operator ($\neg$) has highest precedence, followed by $\wedge$, $\vee$, $\Rightarrow$, and $\Leftrightarrow$. Thus,
\[\begin{aligned} \neg A \wedge B & \text{ means }\quad (\neg A) \wedge B \\ A \vee B \Leftrightarrow C & \text{ means}\quad (A \vee B) \Leftrightarrow C \\ \neg A \vee B \wedge C & \text{ means}\quad (\neg A) \vee (B \wedge C) \end{aligned}\]Here, we’ve used parentheses to clarify operator grouping, but parentheses may also be used to group operations as desired (e.g. $\neg (A \wedge B)$), or improve readability (e.g. $(A \wedge B) \vee (C \wedge D) \vee (E \wedge F )$).
The set of sentences that represent our knowledge is called our knowledge base. For example, the knowledge base for our liars and truth-tellers problem is:
\[\{ A \Leftrightarrow \neg B, B \Leftrightarrow \neg C, C \Leftrightarrow \neg A \wedge \neg B \}\]Note that these sentences could all be combined with conjunction in a single sentence which expresses all knowledge of the knowledge base:
\[(A \Leftrightarrow \neg B) \;\wedge\; (B \Leftrightarrow \neg C) \;\wedge\; (C \Leftrightarrow \neg A \wedge \neg B )\]If we think of our atomic sentence symbols as boolean variables, then an assignment to all variables would be called a truth assignment. A truth assignment which makes a sentence $s$ true is said to satisfy $s$. This satisfying truth assignment is also called a model of $s$.
Another way to think about it is that each truth assignment is a “world”, and that the models of $s$ are “possible worlds”. If and only if $s$ has a model, $s$ is said to be satisfiable. If and only if $s$ has no model, $s$ is said to be unsatisfiable. If and only if every truth assignment is a model of $s$, then $s$ is said to be valid or a tautology.
Now let us consider two sentences $S_1$ and $S_2$. We say that $S_1$ entails $S_2$, denoted $S_1 \models S_2$,
if and only if every model of $S_1$ is also a model of $S_2$. Sometimes this is expressed by saying that “$S_2$ logically follows from $S_1$”. Two sentences $S_1$ and $S_2$ are logically equivalent if and only if $S_1 \models S_2$ and $S_2 \models S_1$.
Conjunctive Normal Form (CNF)
Propositional knowledge which is expressed as a conjunction of disjunctions of literals is said to be in conjunctive normal form (CNF). Recall that a literal is an atomic sentence or a negated atomic sentence. A disjunction (or) of literals is often referred to as a clause. Conjunctive normal form is a conjunction (and) of such clauses.
Any sentence can be converted to CNF. We will describe the steps of this process and show how the liar and truth-teller example knowledge base may be converted to CNF.
- Eliminate $\Leftrightarrow$. Replace each occurrence of $S_1 \Leftrightarrow S_2$ with the equivalent $(S_1 \Rightarrow S_2) \wedge (S_2 \Rightarrow S_1)$. Thus, the knowledge base
may be rewritten as
\[\{ (A \Rightarrow \neg B) \wedge (\neg B \Rightarrow A), (B \Rightarrow \neg C) \wedge (\neg C \Rightarrow B), (C \Rightarrow \neg A \wedge \neg B) \wedge (\neg A \wedge \neg B \Rightarrow C) \}\]We noted before that the set of knowledge base sentences could all be combined with conjunction in a single equivalent sentence. At any time, we can use this equivalence in the opposite direction to separate conjunctions into separate sentences of the knowledge base:
\[\{ A \Rightarrow \neg B, \neg B \Rightarrow A, B \Rightarrow \neg C, \neg C \Rightarrow B, C \Rightarrow \neg A \wedge \neg B, \neg A \wedge \neg B \Rightarrow C \}\]- Eliminate $\Rightarrow$. Replace each occurrence of $S_1 \Rightarrow S_2$ with the equivalent $\neg S_1 \vee S_2$. With such replacements, our knowledge base becomes:
- Move $\neg$ inward. In CNF, negation ($\neg$) only occurs in literals before atomic sentence symbols. All occurrences of $\neg$ can either be negated or “moved” inward towards the atomic sentences using three equivalences:
Using these equivalences, our knowledge base is rewritten:
\[\{ \neg A \vee \neg B, B \vee A, \neg B \vee \neg C, C \vee B, \neg C \vee \neg A \wedge \neg B, A \vee B \vee C \}\]- Distribute $\vee$ over $\wedge$. That is move disjunction ($\vee$) inward while moving conjunction ($\wedge$) outward to form a conjunction of disjunctions. This is accomplished through distributivity of $\vee$:
Thus, we can rewrite our knowledge base:
\[\{ \neg A \vee \neg B, B \vee A, \neg B \vee \neg C, C \vee B, (\neg C \vee \neg A) \wedge (\neg C \vee \neg B), A \vee B \vee C \}\]or
\[\{ \neg A \vee \neg B, B \vee A, \neg B \vee \neg C, C \vee B, \neg C \vee \neg A, \neg C \vee \neg B, A \vee B \vee C \}\]This is sometimes more compactly expressed as a set of a set of literals, where the sets of literals are implicitly understood as clauses (disjunctions) and the set of these is implicitly understood as the knowledge base, a conjunction of known sentences:
\[\{ \{\neg A, \neg B \}, \{ B, A\}, \{ \neg B, \neg C\}, \{ C, B \}, \{ \neg C, \neg A \}, \{ \neg C, \neg B \}, \{ A, B, C \} \}\]It is important to note that a model in CNF is a truth assignment that makes at least one literal in each clause true.
Resolution Theorem Proving
Consider the two clauses, $B \vee A$ or ${B,A}$ and $\neg B \vee \neg C$ or ${\neg B,\neg C}$ of our example CNF knowledge base. The first reads, “Bob is a truth-teller or Amy is a truth-teller.” The second reads, “Bob is not a truth-teller or Cal is not a truth-teller.” Consider what happens according to Bob’s truthfulness:
- Bob is not a truth-teller. The second clause is satisfied. The first clause is satisfied if and only if Amy is a truth-teller.
- Bob is a truth-teller. The first clause is satisfied. The second clause is satisfied if and only if Cal is not a truth-teller.
Since one case or the other holds, we know in any model of both clauses that Amy is a truth-teller or Cal is not a truth-teller. In other words, from clauses $B \vee A$ and $\neg B \vee \neg C$, we can derive the clause $A \vee \neg C$ and add it to our knowledge base. This is a specific application of the resolution rule.
In general, we can express the resolution rule as follows: Given a clause $l_1 \vee l_2 \vee \ldots \vee l_n \vee A$ and $l_1 \vee l_2 \vee \ldots \vee l_n \vee \neg A$, we can derive the clause $l_1 \vee l_2 \vee \ldots \vee l_n$. If $A$ is false, one of the other first clause literals must be true. If $A$ is true, one of the other second clause literals must be true. Since $A$ must be either true or false, then at least one of all the other $n$ literals must be true.
Not all possible resolution rule derivations are useful. Consider what happens when we apply the resolution rule to the first two clauses of our example knowledge base. From $\neg A \vee \neg B$ and $B \vee A$, we can derive either $\neg A \vee A$ or $\neg B \vee B$ depending on which atomic sentence we use for the resolution. In either case, we derive a tautology. The clause $\neg A \vee A$ is always true. It reads “Amy is not a truth-teller or Amy is a truth-teller.”
In order to direct our derivations towards a simple goal, we will perform proof by contradiction. The basis of this style of proof is the fact that $S_1 \models S_2$ if and only if $(S_1 \wedge \neg S_2)$ is unsatisfiable. Put another way, every truth assignment that makes $S_1$ true also makes $S_2$ true if and only if there exists no truth assignment where $S_1$ is true and $S_2$ is false.
The application of this principle is simple. Suppose that sentence $S_1$ represents our knowledge base, and that we wish to wish to prove that sentence $S_2$ follows from $S_1$. We simply add $\neg S_2$ to our knowledge base and seek to derive a contradiction. We take what we believe must follow, and prove it by showing that the opposite causes a contradiction. This approach is not only effective in human argument, but is important for automated theorem proving as well.
Let us use this approach to prove that Cal is a liar ($\neg C$). In addition to the knowledge base, we assume the negation of what we wish to prove ($\neg \neg C$, that is $C$). We will number our clauses to the left. To the right, we will list the clause numbers used to derive the clause by resolution.
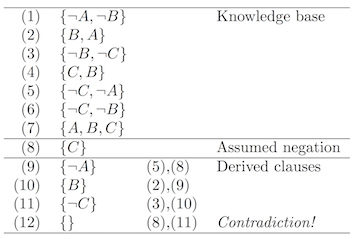
Recall that at least one literal of each clause must be true for a truth assignment to be a model. This last empty clause has no literals at all and represents a clear contradiction. To see why, consider the resolution that led to it. In (10) and (11) we declare a fact and its negation to be true. The resolution rule leaves us no literals to be made true to satisfy these clauses. A clause with no literals is thus logically equivalent to false. Since we hold each clause to be true, we have in effect shown that false is true. This is a contradiction. Thus it cannot be the case that ${C}$ is true as we had assumed. Thus ${\neg C}$ logically follows from our knowledge base.
It should be noted that an unsatisfiable knowledge base will derive an empty clause without any need of assumption. One can thus prove any sentence using proof by contradiction and starting with a contradictory knowledge base.
If one cannot derive a contradiction in this manner, then there is a satisfying truth assignment for the knowledge base and the assumed negation of the hypothesis one sought to prove.
For practice, the reader should perform two resolution proofs by contradiction that
- Amy is a liar, and
- Bob is a truth-teller.
When we derive a sentence $S_2$ from sentence $S_1$, we denote it $S_1 \models S_2$. A proof procedure that derives only what is entailed is called sound. A proof procedure that can derive anything that is entailed is called complete. Resolution theorem proving is both sound and complete.
Part 1: Pacman
The Expr Class
In the first part of this project, you will be working with the Expr class defined in logic.py to build propositional logic sentences. An Exprobject is implemented as a tree with logical operators ($\wedge$, $\vee$, $\neg$, $\rightarrow$, $\leftrightarrow$) at each node and with literals (A, B, C) at the leaves. The sentence
would be represented as the tree.
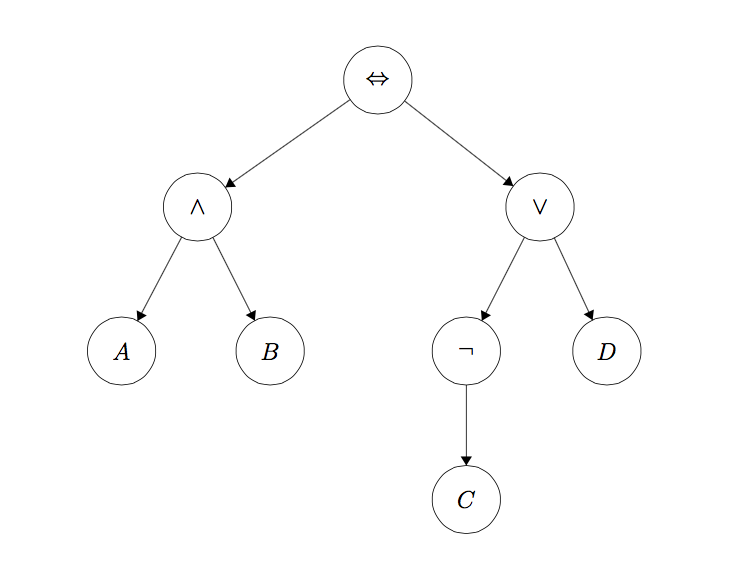
To instantiate a symbol named ‘A’, call the constructor like this:
A = Expr('A')
The Expr class allows you to use Python operators to build up these expressions. The following are the available Python operators and their meanings:
~A: $\neg A$A & B: $A \wedge B$A | B: $A \vee B$A >> B: $A \rightarrow B$A % B: $A \leftrightarrow B$
So to build the expression $A \wedge B$, you would type this:
A = Expr('A')
B = Expr('B')
a_and_b = A & B
(Note that A to the left of the assignment operator in that example is just a Python variable name, i.e. symbol1 = Expr('A') would have worked just as well.)
One last important thing to note is that typing in A & B & C will give the expression ((A & B) & C). If instead you want (A & B & C), as you will for these problems, use conjoin, which takes a list of expressions as input and returns one expression that is the conjunction of all the inputs. Even though both expressions are logically equivalent, it is generally neater to use conjoin everywhere you can, because it is easier to read your knowledge base for debugging when your expression tree is more flat and does not have many layers of nested parentheses. The & operator in Python is a binary operator and builds an unbalanced binary tree if you chain it several times, whereas conjoin builds a tree that is one level deep with all the inputs extending directly from the & operator at the root. disjoin is similarly defined for |. The autograder for Question 1 will require that you use conjoin and disjoin wherever possible, instead of chaining several & operators or several | operators. If you keep with this convention for later problems, it will help with debugging because you will get more readable expressions.
There is additional, more detailed documentation for the Expr class in logic.py.
Tips
- When creating a symbol with
Expr, it must start with an upper case character. You will get non-obvious errors later if you don’t follow this convention. - Be careful about combining
Exprinstances. For example, if you intend to create the expressionx = Expr('A') & Expr('B'), you don’t want to accidentally typex = Expr('A & B'). The former will be a logical expression of the symbol ‘A’ and the symbol ‘B’, while the latter will be a single symbol (Expr) named ‘A & B’.
SAT Solver Setup
A SAT (satisfiability) solver takes a logic expression which encodes the rules of the world and returns a model (true and false assignments to logic symbols) that satisfies that expression if such a model exists. To efficiently find a possible model from an expression, we take advantage of the pycosat module, which is a Python wrapper around the picoSAT library.
Unfortunately, this requires installing this module/library on each machine.
To install this software on your conda env, please follow these steps:
- Activate your conda env (if your env is called
(cs4811)):
(base) [lebrown@c28-112a-01 logic]$ conda activate cs4811- Install pycosat: On command line run:
(cs4811) [lebrown@c28-112a-01 logic]$ conda install pycosatTesting pycosat installation:
After unzipping the project code and changing to the project code directory, run:
(cs4811) [lebrown@c28-112a-01 logic]$ python pycosat_test.pyThis should output:
[1, -2, -3, -4, 5].
Please let us know if you have issues with this setup. This is critical to completing the project, and we don’t want you to spend your time fighting with this installation process.
Q1 (2 pts): Logic Warm-up
This question will give you practice working with the Expr data type used in the project to represent propositional logic sentences. You will implement the following functions in logicPlan.py:
sentence1(): Create oneExprinstance that represents that the following three sentences are true. Do not do any logical simplification, just put them in a list in this order, and return the list conjoined. Each element of your list should correspond to each of the three sentences.
sentence2(): Create oneExprinstance that represents that the following four sentences are true. Again, do not do any logical simplification, just put them in a list in this order, and return the list conjoined.
sentence3(): Using thePropSymbolExprconstructor, create symbolsPacmanAlive[0],PacmanAlive[1],PacmanBorn[0], andPacmanKilled[0](see below for an examplePropSymbolExprinstantiation), and create oneExprinstance which encodes the following three English sentences as propositional logic in this order without any simplification:- Pacman is alive at time 1 if and only if he was alive at time 0 and he was not killed at time 0 or he was not alive at time 0 and he was born at time 0.
- At time 0, Pacman cannot both be alive and be born.
- Pacman is born at time 0.
findModel(sentence): Useto_cnfto convert the input sentence into Conjunctive Normal Form (the form required by the SAT solver). Then pass it to the SAT solver usingpycoSATto find a satisfying assignment to the symbols insentence, i.e., a model. A model is a dictionary of the symbols in your expression and a corresponding assignment of True or False. You can test your code onsentence1(),sentence2(), andsentence3()by opening an interactive session in Python and runningfindModel(sentence1())and similar queries for the other two. Do they match what you thought?
For the later problems in the project, we will have symbols with names like P[3, 4, 2], which represents Pacman being at position (3, 4) at time 2, and we will use them in logic expressions like the above in place of A, B, C, D. The PropSymbolExpr constructor is a useful tool for creating symbols like P[3, 4, 2] that have numerical information encoded in their name. For example, to obtain the symbol P[3,4,2], you would type PropSymbolExpr('P', 3, 4, 2).
Are sentence1(), sentence2(), and sentence3() satisfiable? If so, try to find a satisfying assignment. (This is not graded, but is a good self-check to make sure you understand what’s happening here.)
Before you continue, try instantiating a small sentence, e.g. $A \wedge B \rightarrow C$, and call to_cnf on it. Inspect the output and make sure you understand it (refer to AIMA section 7.5.2 for details on the algorithm to_cnf implements).
To test and debug your code run:
python autograder.py -q q1Q2 (3 pts): Logic Workout
Implement the following three logic expressions in logicPlan.py:
atLeastOne(literals): Return a single expression (Expr) in CNF that is true only if at least one expression in the input list is true. Each input expression will be a literal.atMostOne(literals): Return a single expression (Expr) in CNF that is true only if at most one expression in the input list is true. Each input expression will be a literal. HINT: Useitertools.combinations. If you have n literals, and at most one is true, your resulting CNF expression should be a conjunction of $\binom{n}{2}$ clauses.exactlyOne(literals): Return a single expression (Expr) in CNF that is true only if exactly one expression in the input list is true. Each input expression will be a literal. If you decide to call your previously implementedatLeastOneandatMostOne, callatLeastOnefirst to pass our autograder for q3.
Each of these methods takes a list of Expr literals and returns a single Expr expression that represents the appropriate logical relationship between the expressions in the input list. An additional requirement is that the returned Expr must be in CNF (conjunctive normal form). You may NOT use the to_cnf function in your method implementations (or any of the helper functions logic.eliminate_implications, logic.move_not_inwards, and logic.distribute_and_over_or).
When implementing your planning agents in the later questions, you will not have to worry about CNF until right before sending your expression to the SAT solver (at which point you can use findModel from question 1). to_cnf implements the algorithm from section 7.5.2 in AIMA. However, on certain worst-case inputs, the direct implementation of this algorithm can result in an exponentially sized sentences. In fact, a certain non-CNF implementation of atMostOne is one such worst case. So if you find yourself needing the functionality of atLeastOne, atMostOne, or exactlyOne for a later question, make sure to use the functions you’ve already implemented here to avoid accidentally coming up with that non-CNF alternative and passing it to to_cnf. If you do this, your code will be so slow that you can’t even solve a 3x3 maze with no walls.
You may utilize the logic.pl_true function to test the output of your expressions. pl_true takes an expression and a model and returns True if and only if the expression is true given the model.
To test and debug your code run:
python autograder.py -q q2Q3 (3 pts): Pacphysics and Satisfiability
In this question, you will implement the basic pacphysics logical expressions, as well as learn how to prove where pacman is and isn’t by building an appropriate knowledge base (KB) of logical expressions.
Implement the following functions in logicPlan.py:
pacphysics_axioms: Here, you will add the following axioms topacphysics_sentences. For a given timestep t:- For all (x, y) in
all_coords, add the following implication (if-then form): if a wall is at (x, y), then Pacman is not at (x, y, t) - Pacman is at exactly one of the non_outer_wall_coords at timestep t.
- Pacman takes exactly one of the four actions in DIRECTIONS at timestep t.
- Add each of the sentences above to
pacphysics_sentences.
- For all (x, y) in
check_location_satisfiability: Given a transition (x0_y0, action0, x1_y1, action1) and aproblem, you will write a function that will return a tuple of two models(model1, model2).model1will attempt to prove that givenx0_y0, action0, action1, Pacman is at (x1, y1) at time t = 1.model2will attempt to prove that givenx0_y0, action0, action1, Pacman is NOT at (x1, y1) at time t = 1.- To implement this problem, you will need to add the following expressions to your KB in order:
- At t = 0:
- Add to KB: Pacman’s current location (x0, y0)
- Add to KB:
pacphysics_axioms(...) - Add to KB: Pacman takes
action0 - Add to KB:
allLegalSuccessorAxioms(t+1, ...)
- At t = 1:
- Add to KB:
pacphysics_axioms(...) - Add to KB: Pacman takes
action1
- Add to KB:
- At t = 0:
If you are stuck on check_location_satisfiability, think back on how to prove a knowledge base entails some query q: we prove that $KB \wedge \neg q$ is unsatisfiable. Likewise, to prove some query q is false given a knowledge base, we prove $KB \wedge q$ is unsatisfiable. Thus, your two models should both call findModel, but one on KB $\wedge$ (Pacman at (x1, y1)), and the other on KB $\wedge \neg$ (Pacman at (x1, y1)).
Prop Symbol Names (Important!): For the rest of the project, please use the following variable naming conventions:
PropSymbolExpr(pacman_str, x, y, t): whether or not Pacman is at (x, y) at time tPropSymbolExpr(wall_str, x, y): whether or not a wall is at (x, y)PropSymbolExpr(action, t): whether or not pacman takes actionactionat time t, whereactionis an element ofDIRECTIONS
For the variable that encodes whether or not Pacman is at (x, y) at time t, write the code PropSymbolExpr(pacman_str, x, y, t). For the variable that encodes whether or not a wall is at (x, y), write the code PropSymbolExpr(wall_str, x, y).
Transition Models: In this project, we will use a transition models:
allLegalSuccessorAxioms: This transition model assumes that all actions taken are valid (no action brings pacman onto a square with walls). We will use this function to generate our successor axioms for most of the project, because it is lightweight and improves runtime.
To test and debug your code run:
python autograder.py -q q3Q4 (4 pts): Path Planning with Logic
Pacman is trying to find the end of the maze (the goal position). Implement the following method using propositional logic to plan Pacman’s sequence of actions leading him to the goal:
positionLogicPlan(problem): Given an instance oflogicPlan.PlanningProblem, returns a sequence of action strings for the Pacman agent to execute.
You will not be implementing a search algorithm, but creating expressions that represent pacphysics for all possible positions at each time step. This means that at each time step, you should be adding general rules for all possible locations on the grid, where the rules do not assume anything about Pacman’s current position.
You will need to code up the following sentences for your knowledge base, in the following pseudocode form:
- Add to KB: Initial knowledge: Pacman’s initial location at timestep 0
- for t in range(50) [Autograder will not test on layouts requiring $\geq$ 50 timesteps]
- Add to KB: Initial knowledge: Pacman can only be at
exactlyOneof the locations innon_wall_coordsat timestep t. - Is there a satisfying assignment for the variables given the knowledge base so far?
UsefindModeland pass in the Goal Assertion andKB.- If there is, return a sequence of actions from start to goal using
extractActionSequence. - Here, Goal Assertion is the expression asserting that Pacman is at the goal at timestep t.
- If there is, return a sequence of actions from start to goal using
- Add to KB: Pacman takes exactly one action per timestep.
- Add to KB: Transition Model sentences: call
pacmanSuccessorStateAxioms(...)for all possible pacman positions innon_wall_coords.
- Add to KB: Initial knowledge: Pacman can only be at
Test your code on smaller mazes using:
python pacman.py -l maze2x2 -p LogicAgent -a fn=plppython pacman.py -l tinyMaze -p LogicAgent -a fn=plpTo test and debug your code run:
python autograder.py -q q4Note that with the way we have Pacman’s grid laid out, the leftmost, bottommost space occupi-able by Pacman (assuming there isn’t a wall there) is (1, 1), as shown below (not (0, 0)).
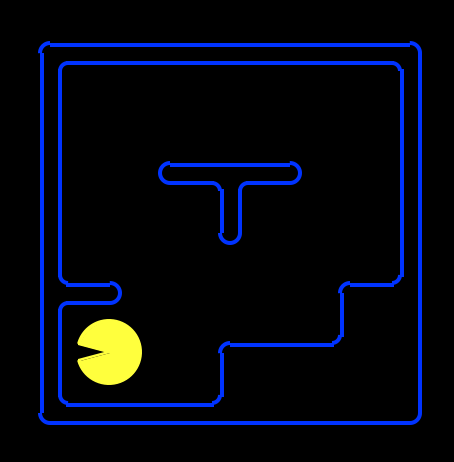
Hint: If you are stuck, try re-reading AIMA chapter 7.7, “Agents Based on Propositional Logic.”
Debugging hints:
- If you’re finding a length-0 or a length-1 solution: is it enough to simply have axioms for where Pacman is at a given time? What’s to prevent him from also being in other places?
- Coming up with some of these plans can take a long time. It’s useful to have a print statement in your main loop so you can monitor your progress while it’s computing.
- If your solution is taking more than a couple minutes to finish running, you may want to revisit implementation of
exactlyOneandatMostOne(if you rely on those), and ensure that you’re using as few clauses as possible.
Part 2: Liars
Q5 (3 pts): Liars and Truth-Tellers
This problem is from the Ontario Mathematical Gazette 22.1.1. Consider and encode the following problem.
The salt has been stolen! Well, it was found that the culprit was either the Caterpillar, Bill the Lizard or the Cheshire Cat. The three were tried and made the following statements in court: CATERPILLAR: Bill the Lizard ate the salt. BILL THE LIZARD: That is true! CHESHIRE CAT: I never ate the salt.
As it happened, at least one of them lied and at least one told the truth. Who ate the salt?
For Question 5, you will fill in five methods in liars.py. Each method corresponds to one of the five axioms described by the problem:
- CATERPILLAR statement
- BILL THE LIZARD statement
- CHESHIRE CAT statement
- at least one of them lied and at least one of them told the truth
- one of them ate the salt.
Use the following encoding of the propositions:
- Let
1be CATERPILLAR tells the truth - Let
2be BILL THE LIZARD tells the truth - Let
3be CHESHIRE CAT tells the truth - Let
4be CATERPILLAR ate the salt - Let
5be BILL THE LIZARD ate the salt - Let
6be CHESHIRE CAT ate the salt
Your program is expected to return a nested list representing the CNF form of the statement.
Clauses (disjunctions) are specified as a list of integer literals, each representing a propositional variable. If the integer is positive, we are referring to the literal directly. If the integer is negative, we treat it as the not of the literal. The clause ``The CATERPILLAR does not tell the truth or BILL THE LIZARD does not tell the truth’’ would be represented by the python list [-1, -2].
Clauses are then combined together as a list. A knowledge base with the sentence above combined with another sentence, ‘‘CATERPILLAR ate the salt or CHESHIRE CAT did not eat the salt’’ would be: [[-1, -2], [4, -6]]. The return value for a CNF statement will always be a nested list of depth two.
Grading: The autograder will test each axiom and will ensure that the axioms have a correct structure and use the correct atomic statements. Finally, the autograder will test the inference of the entailment statement (KB entails 1, KB entails -1, KB entails 2, etc.) to ensure that the axioms are correct.
python autograder.py -q q5Part 3: Clue
Clue (also known as Cluedo in some regions) is a mystery-themed game of deduction. The goal of the game is to be the first player to correctly name the contents of a case file: the murder suspect, the weapon used, and the room the murder took place in. There are 6 possible suspects, 6 possible weapons, and 9 possible rooms, each of which are pictured on a card. One card of each type is chosen randomly and placed in a “case file” envelope without being revealed to any player. All other cards are dealt out face-down to the players. Each player takes on the identity of one of the suspects.
Each player thus begins with private knowledge: that their dealt cards are not in the case file. As the game proceeds, players suggest possible suspect, weapon, and room combinations, and other players refute these suggestions by privately revealing such cards to the suggester. This type of game is called a knowledge game, and the basic knowledge of the game may be expressed using propositional logic.
Reasoning about Clue
In this section, we describe the skeleton implementation of cluedo.py which maintains a knowledge base of Clue game information. Portions of the implementation which supply clauses to the autograder are deliberately left unimplemented as exercises for you. When these portions are implemented, expert deductions can be made about the game.
In cluedo.py, there is a class which encapsulates the card identifiers we will be used. We also provide you with static methods which should be used to translate card identifiers to the corresponding integer identifiers:
1
2
3
4
5
6
suspects = ["mu", "pl", "gr", "pe", "sc", "wh"]
weapons = ["kn", "ca", "re", "ro", "pi", "wr"]
rooms = ["ha", "lo", "di", "ki", "ba", "co", "bi", "li", "st"]
caseFile = "cf"
hands = suspects + [caseFile]
cards = suspects + weapons + rooms
- suspects a list of symbols representing the suspects
- weapons a list of symbols representing the weapons
- rooms a list of symbols representing the rooms
- caseFile the symbol representing the case file
- hands a list of all the hands (all the locations that a card can be)
- cards a list of all the cards
For our purpose, we assume that all games of Clue have six players, and each player takes on the role of one of the suspects. Also, the suspects list is given in turn order.
The symbols used to represent cards and players are, for the most part, the first two letters of their names, as shown in the following table:
| Players/Suspects | Weapons | Rooms |
Col. Mustard mu |
Knife kn |
Hall ha |
Prof. Plum pl |
Candlestick cs |
Lounge lo |
Mr. Green gr |
Revolver re |
Dining Room di |
Mrs. Peacock pe |
Rope ro |
Kitchen ki |
Miss Scarlett sc |
Lead Pipe pi |
Ballroom ba |
Mrs. White wh |
Wrench wr |
Conservatory co |
Billiard Room bi |
||
Case File cf |
Library li |
|
Study st |
The next functions use the indices (position numbers) of these symbols in their respective lists to compute unique literal integers for clauses.
There is an atomic sentence for each place and card pair. Each Clue atomic sentence $c_p$ symbolizes the statement “The card $c$ is in place $p$.”. We assign an integer to each sentence using the functions:
def getIdentifierFromIndicies(hand,card)
def getIdentifierFromNames(hand,card)
For example, consider the atomic sentence $pi_{wh}$. The player Mrs. White (“wh”) has index 2. The lead pipe card (“pi”) has index 10. There are 21 cards. Therefore, the integer corresponding to the atomic sentence $c_p$ is $2 \times 21 + 10 + 1 = 53$. Each atomic sentence has a unique number.
Q6 (1 pts): Initial Hand
At the beginning of the game, the player is dealt a hand (set) of cards. This is private information the player has about what is not in the case file. Before the beginning of the game, we use the hand function to note that the given cards are in the possession of that player.
deal(player,cards):Grading: The autograder will ensure that the dealt cards correspond to the correct facts in the knowledge base.
python autograder.py -q q6Q7 (4 pts) Game Axioms in KB
Now we come to the portions of the cluedo.py that are the core of the cludeo part of the project. Here you must consider the knowledge to be represented, and construct a list of suitable clauses for the SAT-solver.
The knowledge you will encode falls into four categories:
- Each card is in at least one place. That is, each card is in a player’s hand or the case file. We do not allow the possibility that a card was accidentally left in the box.
axiom_card_exists() - Each card is in at most one place, (if a card is one place, it cannot be in another place) Since there is only one of each card, the fact that it is in one place means in cannot be in another place. For each pair of places, it cannot be in both.
axiom_card_unique() - At least one card of each category is in the case file. We choose one card at random from each category to be placed in the case file. For example, at least one of the weapon cards is in the case file.
axiom_casefile_exists() - At most one card of each category is in the case file (no two cards in each category are in the case file) Since only one card from each category is placed in the case file, we cannot, for example, have both the Pipe
piand Wrenchwrin the case file. For each pair of cards within a category, at least one of the two must not be in the case file.
axiom_casefile_unique()
You should seek to represent some of these facts on paper in propositional logic and convert them to CNF in order to gain a good understanding of what clauses need to be constructed.
HINT: Also think back to Question 2 and your responses there.
Grading: The autograder will test each axiom and will ensure that the axioms have a correct structure and use the correct atomic statements. This does not necessarily mean that the axioms are exactly correct (this will be verified later in Question 10).
python autograder.py -q q7Q8 (4 pts) Game Play - Suggest
Earlier, we noted that the turn order of the players list is important. The suggest function is where this information is used. In the game of Clue, a player may suggest a suspect, a weapon, and a room, upon entering that room on the board. Since the board movement is irrelevant to the deduction, we will not detail the circumstances of a suggestion here.
When a suggestion of three cards is made, the player to the left of the suggester (clockwise) checks their private cards to see if any of the cards are part of the suggestion. If so, the player must refute the suggestion by privately showing one of these refuting cards to the suggester. If not, the player states that they cannot refute the suggestion, and attention then turns to the next player clockwise. The next player does the same, either refuting or not, and this continues clockwise until the first possible refutation, or until all other players have stated that they cannot refute the suggestion.
Suppose all six players are playing with the following turn order: Scarlett, Mustard, White, Green, Peacock, Plum. There are three cases which can occur which will affect the type of knowledge we can from the suggestion:
-
The meaning of the function call
suggest("sc", "wh", "pi", "ha", "pe", "ha")is as follows:suggesterMiss Scarlett suggested that Mrs. White committed the murder with the lead pipe in the hall (parameterscard1,card2, andcard3). This was refuted byrefuterMrs. Peacock, who showed Scarlett the hall card (cardShown).
Consider that we learn much more than the fact that Mrs. Peacock has the hall card. After Scarlett suggested {wh,pi,ha}, all players between Scarlett and the refuter Peacock must have been unable to refute the suggestion. Thus, we also learn that these players, Mustard, White, and Green, do not have any of these cards. The knowledge we gain from a suggestion is both negative, which players do not have the suggested cards, and positive, which card a player has. -
In many cases, a player does not get to see the card that is shown to refute the suggestion. In this case, the
cardShownparameter is given the valueNone. Consider the function callsuggest("wh", "mu", "re", "ba", "pe", None). White suggests that Mustard committed the murder with the revolver in the ballroom. Peacock refutes the suggestion by showing a card privately to White, but the player (Scarlett) does not get to see this card. In this case, we learn that Green does not have these cards. We also learn that Peacock has at least one of these cards. The information gained is similar to the previous case. The difference is that at least one of the three suggested cards must be in the refuter’s hand. -
In some cases, there may not be a refuter at all. This is indicated by having the
refuterparameter with the valueNone. (ThecardShownparameter should then also beNone.) If no player can refute the suggestion, we simply gain information that all players except the suggester do not have the suggested cards. The suggester is never part of the refutation.
Implementing suggest, you must bear all of these cases in mind. Detailed rules to Clue may be found at the Hasbro website and at Wikipedia.
suggest(suggester,card1,card2,card3,refuter,cardShown):Grading: The autograder will ensure that the uncovered facts and knowledge by the suggestion are added to the knowledge base
python autograder.py -q q8Q9 (2 pts) Game Play - Accuse
The winner of Clue is the first player to correctly make an accusation (not a suggestion) naming the three cards in the case file. Each player can make an accusation on any one turn, and checks the correctness of the declared accusation by privately looking in the case file. An accusation can only be made once, as the player either wins or loses depending on the correctness of the accusation. (If a player loses through incorrect accusation, the player continues to refute suggestions by other players, but may no longer take part in play otherwise.)
Consider the example function call accuse("sc, "pe", "pi", "bi", True).
-
This represents the fact that the
accuserScarlett accused Mrs. Peacock of committing the murder with the pipe in the billiard room, and that this accusation is correct (parameterisCorrectisTrue). From a correct accusation, we gain knowledge that these three cards (parameterscard1,card2, andcard3) are in the case file. -
Now consider what happens when the accusation is not correct. Suppose we have the function call
accuse("sc", "pe", "pi", "li", False). Then we learn that at least one of the three cards of the accusation is not in the case file. In implementing accuse, the programmer must handle both of these cases.
Note further that whether the accusation is correct or not, one can deduce that the accuser does not have in hand any of the cards involved in the accusation. A player might suggest cards that are in hand in order to throw others off the trail, but a false accuse results in losing the game.
accuse(accuser,card1,card2,card3,isCorrect):Grading: The autograder will ensure that the uncovered facts and knowledge by the suggestion are added to the knowledge base.
python autograder.py -q q9Q10 (4 pts) Game Play - Full Game
Finally, a full game of Clue is played out accordingly using the specification in cluedo_game.py. This simulates a full game, with the agent taking the role of Ms. Scarlett. This will combine the implementations from the past four questions in order to test if correct deductions can be made on the whole.
Grading: The auto-grader simulates the game is described in the play_cluedo function and checks if the final casefile deduction is correct.
python autograder.py -q q10The game can also be run directly, with debugging output:
python cluedo_game.pyYou are free to modify this code as you wish for your debugging purposes. The printNotebook method might be helpful for debugging the deductions made throughout the game. However, the autograder is configured to use cluedo_game.py directly, so any changes will be reflected in the autograder output. Instead, I recommend that you copy cluedo_game.py and make modifications in the copy.
Submission
You’re not done yet!
Create a single zip-file: project3.zip, that contains the three code files: logicPlan.py, liars.py, and cluedo.py as well as your group information file: group.txt. Submit this zip-file on Canvas .
The file group.txt should be structured as follows:
- a group of size 1
Jane Doe, jdoe1
- a group of size 2
Sherlock Holmes, sholmes John Watson, jwatson
- a group of size 3
Hermione Granger, hgranger Harry Potter, hpotter Ronald Weasley, rweasley