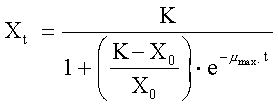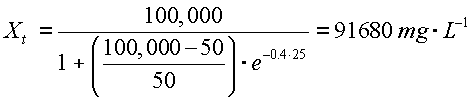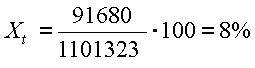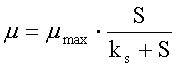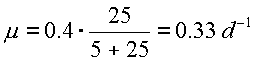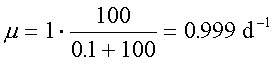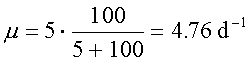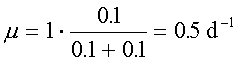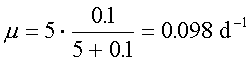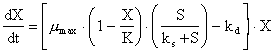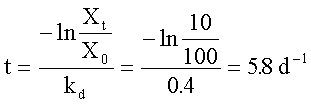CE3501 Environmental Engineering Fundamentals
Environmental
Biology - Homework Assignment #1
1. Mathematical models are used
to predict the growth of a population, i.e. population size at some future
date. The simplest model is that for
exponential growth. The calculation requires
a knowledge of the organism's maximum specific growth rate (μmax). A value for this coefficient can be obtained
from field observations of population size or from laboratory experiments where
population size is monitored as a function of time:
|
Time
(d)
|
Biomass
(mg/L)
|
|
0
|
50
|
|
1
|
75
|
|
2
|
111
|
|
3
|
166
|
|
4
|
248
|
|
5
|
369
|
Calculate μmax
for this population assuming exponential growth; include appropriate units. (0.4d-1)
2. Once a value for μmax has been obtained, the
model may be used to project population size at a future time. Assuming that exponential growth is
sustained, what will the population size in Problem #1 be after 25 days? (1,101,323 mg/L)
3. Exponential growth cannot be
sustained forever because of constraints placed on the organism by its
environment, i.e. the system's carrying capacity. This phenomenon is described using the logistic growth
model. Calculate the size of the
population in Problem #1 after 25 days, assuming that logistic growth is
followed and that the carrying capacity is 100,000 mg/L. What percentage of the exponentially-growing
population size would this be? (91,680 mg/L; 8%)
4. Food limitation of population
growth is described using the Monod model.
Population growth is characterized by the maximum specific growth rate
(μmax) and the half-saturation constant for growth (ks). Calculate the the specific growth rate
(μ) of the population in Problem #1 growing at a substrate concentration
of 25 mg/L according to Monod kinetics with a ks of 50 mg/L. What
percentage of the growth rate (μ) for an exponentially-growing population
would this be? (0.33 d-1; 83%)
5. The two coefficients defined in Problem #4 (μmax
and ks) describe the organism's ability to function in the
environment. Populations with a high
μmax grow rapidly and take up substrate very fast. Those with a low ks are able to
take up substrate quite efficiently, reducing it to low levels. These characteristics are important when
considering the use of microorganisms to clean up pollution from potentially
toxic chemicals. Consider two
genetically engineered organisms intended for use in a chemical spill
cleanup. Organism "A" has a
μmax of 1 d-1 and a ks of 0.1 mg/L. Organism "B" has a μmax
of 5 d-1 and a ks of 5 mg/L. Chemical levels are initially on the order of 100 mg/L; the goal
is to reduce concentrations to below 0.1 mg/L.
We wish to use the organisms in sequence - first one organism to rapidly
reduce chemical levels before they can spread and second, an organism to reduce
chemical levels to the target concentration of 0.1 mg/L. Which organism ("A" or
"B") would be most effective in rapidly
reducing levels of pollution? Which
organism ("A" or "B") would be most effective in reducing the pollutant to trace levels? Back your answer up with calculations. (B is
effective in achieving fast reductions; A reduces pollutants to lower levels)
6. In wastewater treatment, organism
biomass increases as pollutants are taken up and metabolized. This increase is
reflected in the amount of sludge generated at the wastewater treatment plant,
a residue which must receive safe disposal.
Engineers use the yield coefficient (Y) to calculate biomass (sludge)
production. Laboratory studies have
shown that microorganisms produce 10
mg/L of biomass in reducing the concentration of a pollutant by 50 mg/L. Calculate the yield coefficient, specifying
the units of expression. (0.2 mg biomass / mg substrate)
7. When food supplies have been
exhausted, populations die away. This
exponential decay is described by a simple modification of the exponential
growth model. Engineers use this model
to calculate the length of time which a swimming beach must remain closed
following pollution with fecal material.
For a population of bacteria with an initial biomass of 100 mg/L and a kd
= 0.4 d-1, calculate the time necessary to reduce the population
size to 10 mg/L. (5.8 d)
CE3501 Environmental
Engineering Fundamentals
Environmental Biology
Homework Assignment #1 -
Solution Set
1. A
value for μmax may be
calculated using the analytical solution to the exponential growth model:
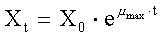
Rearrange the equation to solve
for μmax :
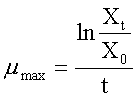
and perform the calculation using
any two measures of biomass and the associated time:
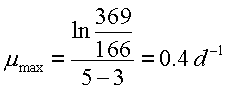
Alternatively, the exponential
growth model could have been log-linearized:
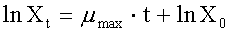
and, using all of the data, a
plot of lnXt versus t would yield μmax as the slope.
2. Again, using the exponential
growth model and the values for μmax determined in Problem #1:
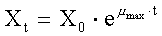
with X0 = 50 mg·L-1,
t = 25 days, and μmax = 0.4 d-1:
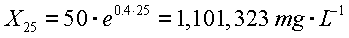
3. The population size after 25 days according to the logistic
growth model can be calculated using
the analytical solution:
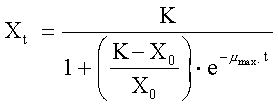
with K = 100,000 mg·L-1
and X0, μmax, and t as above:
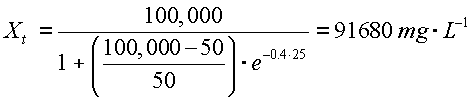
which is:
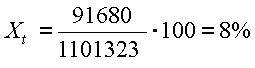
of the biomass calculated
according to the exponential growth model.
4. The specific growth rate for a population growing under nutrient
limited conditions can be calculated using the Monod model:
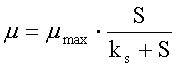
For a μmax of 0.4 d-1 from Problem #1 and
values of S = 25 mg·L-1
and ks = 5 mg·L-1, as provided here, the specific growth
rate would be:
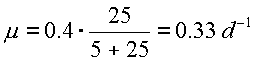
or 0.33/0.4 = 83% of the growth rate
for the exponentially-growing population.
5. Here we wish to compare the
growth rates, calculated as in Problem #4, for two organisms ("A" and
"B") under tow different sets of conditions: (1) immediately following
a pollutant spill when concentrations are high, e.g. 100 mg·L-1,
and we wish to quickly stop pollutant migration and (2) later in the cleanup
effort when concentrations are low, e.g. 0.1 mg·L-1, and are
approaching the target concentration.
Again, we use the Monod model:
At a 100 mg·L-1
pollutant level:
Organism A –
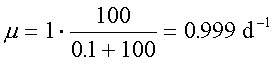
Organism B –
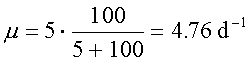
At a 0.1 mg·L-1
pollutant level:
Organism A –
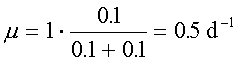
Organism B -
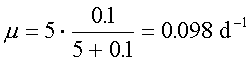
Thus it can be seen that Organism
B has the fastest growth rate at high pollutant concentrations and would be
most effective in rapidly reducing pollutant levels and that Organism A has the
fastest growth rate at low pollutant levels and would be most effective in
reducing the pollutant to trace levels.
6. The yield coefficient is
defined as the amount of biomass produced per unit substrate consumed:
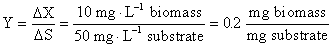
7. Under conditions of exhausted food
supplies (S=0), the overall population growth model:
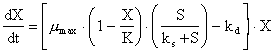
reduces to:
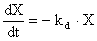
which has the analytical
solution:
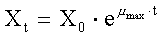
substituting, X0 = 100
mg·L-1,
Xt = 10 mg·L-1, and kd = 0.4 d-1,
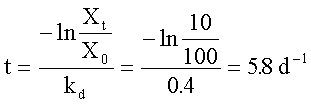
![]()
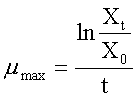
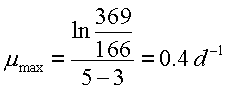
![]()
![]()
![]()