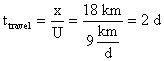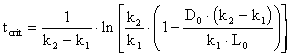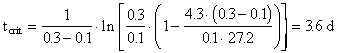CE3501 Environmental Engineering

Homework Assignment #2

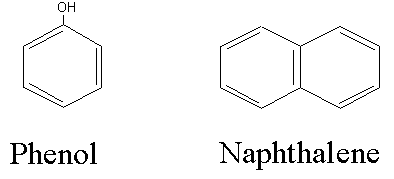
1. Organic carbon, C(H₂O), and ammonia nitrogen, NH₃-N, are oxidized to carbon dioxide (CO₂) and nitrate (NO₃), respectively, by the bacteria which are naturally present in wastewater and in natural systems such as lakes and rivers. Both of these reactions consume oxygen and thus cause a negative impact on water quality. The amount of oxygen theoretically required to oxidize a carbonaceous or nitrogenous waste (its ThOD) may be calculated according to the stoichiometry of the reactions as outlined in class. The production of coke, a fuel produced from coal for use in steel mills, generates a waste stream rich in ammonia, phenol, and naphthalene. Calculate the carbonaceous ThOD and the nitrogenous ThOD of a waste containing 25 mg/L of ammonia nitrogen (NH₃-N), 50 mg/L of phenol (C₆H₅OH) and 150 mg/L of naphthalene (C₁₀H₈).

2. How much oxygen is actually consumed depends on the extent to which the waste is biodegradable, i.e. amenable to oxidation by microbes. Ammonia is totally biodegradable and thus the nitrogenous ThOD (theoretical) and the nitrogenous BOD (actual) are equal. Not so for carbonaceous compounds: the carbonaceous BOD (actual) may be significantly less than the carbonaceous ThOD (theoretical) if the compound is poorly degradable. The 5-day CBOD test, interpreted to yield a value for the ultimate CBOD, provides an estimate of the amount of oxygen which a waste will actually consume. The waste in Problem #1 was found to have a 5-day CBOD of 90 mg/L and a rate constant (k_L) of 0.1d^-1. Calculate the ultimate CBOD of the waste.

Another test, chemical oxygen demand (COD), uses strong chemical agents to completely oxidize the waste. Thus COD values are comparable to ThOD estimates. Your text (Section 5.4.7) explains how a comparison of COD and CBOD values can provide information on a waste's tendency to biodegrade. Assuming equivalent ThOD and COD values, comment on the biodegradability of this waste.

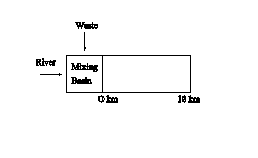
3. In order to evaluate the impact of a waste on a receiving water, we must calculate the concentration of the waste as it mixes with the stream and how that concentration changes as the waste moves downstream, degrading as it travels. The first step involves a CMFR analysis at the mixing basin and the second applies first-order kinetics in a plug flow reactor. The steel mill waste described in Problem #1 is discharged at a rate of 0.75 m³/s; the waste has a dissolved oxygen (DO) concentration of 3 mg/L. The river receiving the waste has a flow of 6 m³/s and travels at a velocity of 9 km/day. The river has an ultimate CBOD of 2 mg/L, an NH₃-N concentration of 0.5 mg/L and a dissolved oxygen (DO) concentration of 6 mg/L upstream of the discharge. Assume a value for k_L as in Problem #2 and that k_N = 0.15 d^-1. Calculate the NBOD (14.7 mgO₂/L), the ultimate CBOD (27.2 mgO₂/L) and DO (5.7 mgO₂/L) of the river immediately after it becomes mixed with the waste and the 5-day (8.8 mgO₂/L), ultimate (22.3 mgO₂/L) CBOD, NBOD (10.9 mgO₂/L) and NH₃-N concentration (2.4 mgN/L) 18 km downstream of the point of discharge.

4. As the waste moves downstream, exertion of the oxygen demand removes oxygen from the water and exchange with the air (reaeration) adds oxygen to the water. Initially exertion exceeds reaeration and the dissolved oxygen (DO) content of the water drops. Later, as the waste becomes stabilized (no longer consuming as much oxygen), the river DO increases. The result is a dissolved oxygen sag curve. Equations were provided in class to determine the location and value for the minimum point in the DO sag curve. Using data from Problem #3 and assuming that there is no NBOD exertion, calculate the oxygen deficit, D_o, in the river (4.3 mgO₂/L) after it has mixed completely with the waste discharge and the time (3.6 d), location (32.4 km), and value of the maximum deficit (6.3 mgO₂/L) and minimum DO (3.7 mgO₂/L). Assume a saturation DO for the river of 10 mg/L, that k₁ = k_L, and that the reaeration coefficient (k₂) is 0.3 d^-1.

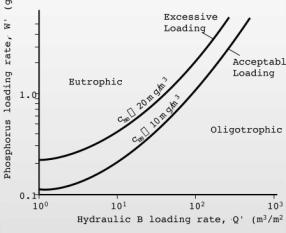
5. A lake with a surface area of 1x10⁶ m², a depth of 10m, and an inflow of 2x10⁷ m³·yr^-1 receives phosphorus inputs from a wastewater treatment plant of 1.5x10⁶ gP·yr^-1. Calculate the steady state phosphorus concentration in the lake (0.05 gP·m^-3) assuming a settling velocity of 10 m·yr^-1. Determine the % reduction (60%) in phosphorus loading required to bring the lake into mesotrophy. Identify the location of the lake’s trophic status on a copy of a Vollenweider Plot (Figure 5-38) before and after reduction in phosphorus loads.

CE3501 Environmental Engineering Fundamentals

Environmental Biology

Homework Assignment #2 - Solution Set

1. The theoretical nitrogenous oxygen demand, ThNOD, is estimated from the stoichiometry of the nitrification reaction,

where it can be calculated that 4.57 mgO₂ are required for each mgNH₃-N oxidized. Thus,

For the carbonaceous oxygen demand, ThCOD, we need to balance the equations. First for phenol,

We require 7 moles or 224 gO₂ for each mole of phenol. Therefore,

and for napthalene,

We require 12 moles or 384 gO₂ for each mole of napthalene. Therefore,

The overall ThCOD is 450 + 119 = 569 mgAL^-1 and the total theoretical oxygen demand (ThOD) of the waste is 114 + 569 = 683 mgAL^-1.

2. The 5-day CBOD (y₅), oxygen demand exerted after 5 days, is the common laboratory measurement of CBOD. We often want to calculate the ultimate CBOD (L) from the 5-day value and this is done using the equation below,

Inserting the measured y₅ and k_L values, as specified in the problem statement,

This waste would be considered to be poorly degradable because only 40% (229/569) of the ThCOD is exerted.

3. The solution to this problem involves a mixing basin calculation, determination of BOD decay with distance downstream, and conversion among the various measurements of BOD. First, examine a schematic of the stream,

Flow in the mixing basin is given as the sum of the river and waste flows,

The mixing basin calculation for DO is,

A similar calculation is performed for NBOD, using the ThNOD value for the waste as calculated in Problem #1 (NBOD = ThNOD) and the NBOD of the river upstream of the waste input, as calculated from the specified upstream NH₃-N concentration,

to perform the mixing basin calculation,

The ultimate CBOD of the waste (229 mgAL^-1) was determined in Problem #2 and the ultimate CBOD of the river (2 mgAL^-1) is given. The mixing basin CBOD is,

The ultimate CBOD and NBOD downstream can be calculated as a simple exponential decay,

where t = time of travel downstream calculated as,

The ultimate CBOD remaining at 18km is,

which corresponds to a 5-day CBOD of,

The NBOD remaining at 18km is,

and the corresponding NH₃-N is,

4. The first step in calculating the critical distance and the deficit at that point is to determine the initial deficit,

inserting the measured calculated mixing basin DO (5.7 mgAL^-1) from Problem #2 and the value for

for DO_sat specified in the problem statement (10 mgAL^-1),

Then utilizing the equation for the critical distance,

with specified values for k₁ = 0.1, k₂ = 0.3 and with the mixing basin L₀ as determined in Problem #2 (27.2 mgAL^-1),

the corresponding distance is calculated from a knowledge of the river velocity,

The deficit at this location can be calculated from,

with all inputs as described above,

and the corresponding oxygen concentration is given by,

which for the specified DO_sat and the calculated D, yields,

5. The steady state phosphorus concentration is given by:

For the new Css (0.20 gP·m^-3, the mesotrophic boundary), the load is given by:

a 60% reduction.

For plotting, Q’ = 2x10⁷ / 1x10⁶ = 20 m³·m^-2·yr^-1, W_old = 1.5x10⁶ / 1x10⁶ = 1.5 gP·m^-2·yr^-1, and W_new = 0.6x10⁶ / 1x10⁶ = 0.6 gP·m^-2·yr^-1.