pss/RRN-01-021 |

|
Fractal Dislocation Patterning in Plastically Deformed NaCl
Polycrystals
M. Zaiser (a,b), S. Marras (a), E. Nadgorny (a), H.P.
Strunk (c), and E.C. Aifantis (a)
(a) Michigan Technological University, Houghton, MI 49931,
USA
(b) Max-Planck-Institut für Metallforschung,
Heisenbergstr. 1, D-70569 Stuttgart, Germany
(c) Universität
Erlangen, Inst. für Werkstoffwissenschaften, Cauerstr. 6,
D-91058 Erlangen, Germany
(Received May 3, 2001; accepted May 11, 2001)
Subject
classification: 61.72.Lk; 62.20.Fe; S9.11
Introduction
In severely deformed metals, strain hardening goes along with the
formation of cellular dislocation patterns. When many slip systems
are active, these patterns exhibit multiscale behaviour: they are
characterized by power-law distributions of cell sizes [1] and the cell
arrangement has features of a self-similar `hole fractal'. Fractal
cell patterning has been observed in fcc metals deformed in tension
or compression along the [100] and [111] axes [1, 2] as well as in fcc polycrystals [3, 4]. For a general
discussion of different types of dislocation patterns see [5].
In the present research note we report results of a fractal
dimension analysis performed on dislocation cell patterns developing
during severe deformation of polycrystalline NaCl. (For sample
preparation and work-hardening behavior see [6].) The samples were deformed in
compression at room temperature at a strain rate of
10–5s–1. Cellular patterns were observed
inside the grains after deformation to a flow stress of 35.2 MPa
(Fig. 1). The statistical characterization of these patterns is the
subject of the present note.

Figure
1. Dislocation pattern in a grain of a NaCl polycrystal
deformed at room temperature to a flow stress of 35.2 MPa
(the adjacent grains are out of contrast)
Image Analysis and
Results
TEM images of dislocation cell patterns such as the example shown
in Fig. 1 were binarized and the resulting black-and-white patterns
were analyzed using the box counting and correlation integral (`mass
dimension') methods. For the box counting method, the cell pattern
is covered with a grid of meshlength 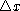 and the number and the number 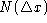 of `boxes' which intersect the cell walls is plotted
double-logarithmically vs. of `boxes' which intersect the cell walls is plotted
double-logarithmically vs. 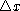 . For the correlation integral method, one determines the
integral M(r) of the pattern autocorrelation function
over a circle of radius r. This is proportional to the
average number of black pixels contained in a circle of radius
r around a black pixel chosen at random. For a fractal
pattern of dimension D, the correlation integral increases as . For the correlation integral method, one determines the
integral M(r) of the pattern autocorrelation function
over a circle of radius r. This is proportional to the
average number of black pixels contained in a circle of radius
r around a black pixel chosen at random. For a fractal
pattern of dimension D, the correlation integral increases as
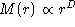 while the number of boxes
decreases as while the number of boxes
decreases as 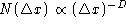 . A detailed discussion of
different methods of fractal dimension analysis applied to
dislocation patterns is found in [2], and the relations between the fractal
dimension D, which characterizes the distribution of length
scales in the dislocation network, and more conventional
characteristics of cell structures such as mean cell size and cell
wall volume fraction are discussed in [2, 7]. . A detailed discussion of
different methods of fractal dimension analysis applied to
dislocation patterns is found in [2], and the relations between the fractal
dimension D, which characterizes the distribution of length
scales in the dislocation network, and more conventional
characteristics of cell structures such as mean cell size and cell
wall volume fraction are discussed in [2, 7].
Figure
2. Mass dimension analysis of TEM micrographs of cell
structures in NaCl. The lower graph has been obtained from the
micrograph shown in Fig. 1; for better visibility, the graphs
have been shifted vertically
Results of the mass dimension analysis of two different
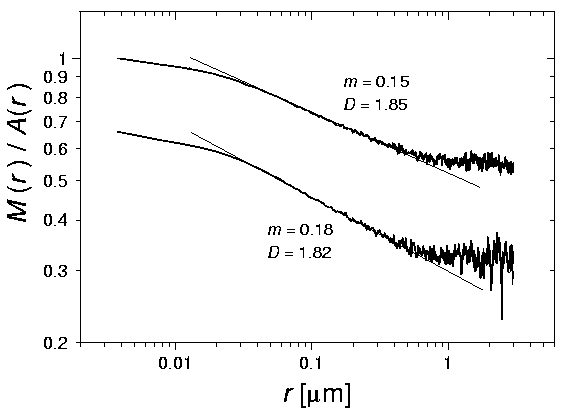
micrographs taken from the same sample are shown in Fig. 2. To
enhance variations in slope, M(r) has been divided by
the area 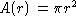 . .
When 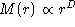 , the slope of the
double-logarithmic plot of (M(r)/A(r))
vs. r is m = D – 2. Accordingly, the analyzed
micrographs yield mass dimensions , the slope of the
double-logarithmic plot of (M(r)/A(r))
vs. r is m = D – 2. Accordingly, the analyzed
micrographs yield mass dimensions 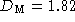 and and 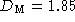 . The linear scaling
regimes in the log–log plots extend in both cases over about one and
a half orders of magnitude. The dimensions obtained by box counting
from the same two micrographs are . The linear scaling
regimes in the log–log plots extend in both cases over about one and
a half orders of magnitude. The dimensions obtained by box counting
from the same two micrographs are 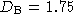 and and 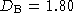 , respectively. Hence
both methods yield fractal dimensions around 1.8 which is close to
the values that have been observed in high-symmetry orientated Cu
single crystals [1, 2]. , respectively. Hence
both methods yield fractal dimensions around 1.8 which is close to
the values that have been observed in high-symmetry orientated Cu
single crystals [1, 2].
Discussion and
Conclusions
Fractal cell patterns have been observed previously in
high-symmetry orientated fcc single crystals and in fcc
polycrystals. In these materials deformation is characterized by the
simultaneous activity of a large number of slip systems. The
deformation behaviour of NaCl polycrystals has many similarities
with this situation [6]: While alkali halide single crystals
usually exhibit macroscopic single glide on {110} glide planes, NaCl
crystals deformed in [111] directions and NaCl polycrystals exhibit
extensive glide on auxiliary slip planes (e.g. {111} or {100}) [6, 8]. The
dislocation network is characterized by the presence of Burgers
vectors of all orientations in approximately equal amounts, and the
flow stress is governed by a forest mechanism [6]. All these findings are very similar to
the situation in [100] or [111] orientated fcc single crystals or in
fcc polycrystals. The observation of fractal cell patterns in NaCl
polycrystals demonstrates that such patterns are not confined to fcc
metals and at the same time corroborates the conjecture [9] that a large
number of active slip systems is a necessary prerequisite for this
type of dislocation patterning.
References
- [1]
- P. HÄHNER, K. BAY, and M.
ZAISER, Phys. Rev. Lett. 81, 2470 (1998).
- [2]
- M. ZAISER, K. BAY, and P.
HÄHNER, Acta Mater. 47, 2463 (1999).
- [3]
- J. GIL SEVILLANO, E.
BOUCHAUD, and L.P. KUBIN, Scripta
Metall. Mater. 25, 355 (1991).
- [4]
- J. GIL SEVILLANO, Phys. Scr.
T49, 405 (1993).
- [5]
- M. ZAISER and E.C. AIFANTIS,
Recent Research Developments in Metallurgical and Materials
Science, Vol. 3, Trivandrum (India) 1999 (p. 79).
- [6]
- E.M. NADGORNYI and H.P. STRUNK,
phys. stat. sol. (a) 104, 193 (1987).
- [7]
- M. ZAISER and P. HÄHNER, Mater.
Sci. Eng. A 249, 145 (1999).
- [8]
- H. STRECKER and H. STRUNK, J.
Electron Microsc., Suppl. 26, 645 (1977).
- [9]
- M. ZAISER and P. HÄHNER, Proc.
20th Riso Internat. Symp. on Materials Science, Roskilde (Denmark)
1999 (p. 547).
physica status solidi
Wed May 16
12:43:46 MET DST 2001
Copyright © 2001 WILEY-VCH Verlag
Berlin |