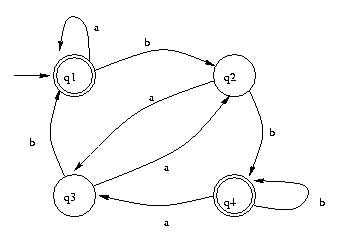

1. (Exercise 1.2) Give a formal description of the machine
pictured below.

2. (Exercise 1.6a) Give state diagrams for DFAs recognizing
the languages below. Then, use the construction given in the proof of
Theorem 1.22 to give the state diagram of an NFA recognizing the union of
these languages.
3. (Exercise 1.7b) Give state diagrams for DFAs recognizing
the languages below. Then, use the construction given in the proof of
Theorem 1.23 to give the state diagrams of an NFA recognizing the
concatenation of
these languages.
4. (Exercise 1.8a) Give state diagram for a DFA recognizing
the language below. Then, use the construction given in the proof of
Theorem 1.24 to give the state diagrams of an NFA recognizing the
star of this language.
5. (Exercise 1.9) Prove that every NFA can be converted to an equivalent one that has a single accept state.
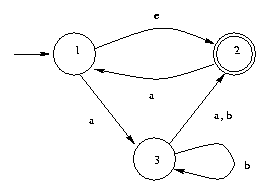
6. (Exercise 1.12b) Use the construction given in Theorem 1.19
to convert the following nondeterministic finite automaton to an
equivalent deterministic finite automaton.
7. (Exercise 1.14a) Use the procedure described in Lemma 1.29
to convert the following regular expression to a nondeterministic finite
automaton.
8. (Exercise 1.16b) Use the procedure described in Lemma 1.32
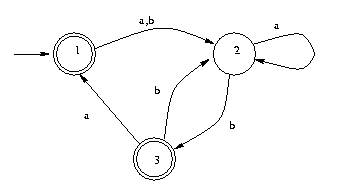
to convert the following finite automaton to a regular expression.
9. (Exercise 1.17c) Use the pumping lemma to show that the following language is not regular.
10. (Exercise 1.18) Describe the error in the following
"proof" that 0*1* is not a regular language. (An
error must exist because 0*1* is regular.) The
proof is by contradiction. Assume that 0*1* is
regular. Let p be the pumping length for
0*1* given by the pumping lemma. Choose
s
to be the string 0p1p. You know that
s is a member of 0*1*, but Example 1.38
shows that s cannot be pumped. Thus you have a contradiction. So
0*1* is not regular.
