a. Is < M,0100 > ∈ ADFA?
b. Is < M,011 > ∈ ADFA?
c. Is < M > ∈ ADFA?
d. Is < M,0100 > ∈ AREX?
e. Is < M > ∈ EDFA?
f. Is < M,M > ∈ EQDFA?


1. (Problem 3.11) A Turing machine with doubly infinite tape is similar to an ordinary Turing machine except that the tape is infinite to the left as well as to the right. The tape is initially filled with blanks except for the portion that contains the input. Computation is defined as usual except that the head never encounters an end to the tape as it moves leftward. Show that this type of Turing machine recognizes the class of Turing-recognizable languages.
2. (Exercise 3.14 b,d,e) Show that the collection of decidable languages is closed under the operations of
3. (Exercise 3.15 b,c,d) Show that the collection of Turing-recognizable languages is closed under the operations of
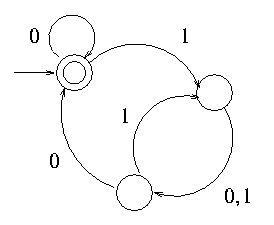
4. (Exercise 4.1) Answer all parts for the following DFA M and
give reasons for your answers.

a. Is < M,0100 > ∈ ADFA?
b. Is < M,011 > ∈ ADFA?
c. Is < M > ∈ ADFA?
d. Is < M,0100 > ∈ AREX?
e. Is < M > ∈ EDFA?
f. Is < M,M > ∈ EQDFA?
