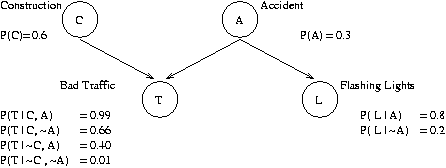
Problem 4: Consider the following BBN
CS4811: Homework 8 --- Reasoning Under Uncertainty (Chapters 5 and 9)
Problem 1:
Consider the following sentences:
1. All final exams are easy.
2. Easy final exams make the students who take them happy.
3. Jane is taking at least one final exam.
4. Someone is happy.
Part a. Represent the above four statements in predicate logic
using
FE (X) for "X is a final exam,"
EASY (X) for "X is easy,"
TAKES (X,Y) for "X takes exam Y,"
H (X) for "X is happy."
Note that the logic formula for the second sentence is given below. Do
not forget to negate the whole premise in parantheses
when you eliminate implication.
∀ Y ∀ Z ( FE(Y) ∧ EASY (Y) ∧ TAKES (Z, Y))
→ H(Z)
Part b. Set up sentences so that the fourth can be proven using
the first three employing resolution refutation. Then convert the
sentences to clause form using the following steps:
1. Eliminate → (implication)
2. Reduce the scope of negation
3. Standardize variables apart
4. Move all quantifiers to the left without changing their order
5. Eliminate existential quantifiers (Skolemize)
6. Drop all universal quantifiers
7. Convert expressions into conjunct of disjuncts form
8. Make each conjunct a separate clause
9. Standardize the variables apart again
Part c. Prove the fourth statement using resolution.
Problem 2:
Consider the following statements:
(a) Write down all the prior and conditional probabilities that you can gather from the above description. Briefly describe the propositions you use.
(b) What is the probability that By-a-rob is walking the dog?
(c) What is the probability that your neighbor is
walking the dog?
Problem 4:
Consider the following BBN

Symbolize and compute the following probabilities:
(a) What is the probability that there is construction, an accident, bad
traffic and flashing lights?
(b) What is the probability that there is no construction, no
accident, no bad
traffic and no flashing lights?
(c) What is the probability of an accident given bad traffic?
(d) What is the probability of an accident given flashing lights?
(e) What is the probability of an accident given construction and
bad traffic?
You are welcome to verify your answers using JavaBayes
(http://www-2.cs.cmu.edu/~javabayes/Home/)
but you should do the computation yourself, and show all the steps of your computation.