Winter 1999-2000

1. (4 points) Below is a diagram of an electrochemical sensor:



 

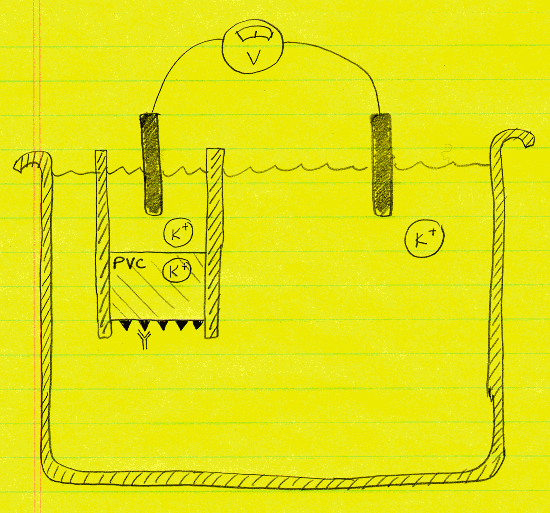
1.a) (1 point) What are the symbols and represent?

(You must explain both to get full credit)

: Antigen (AGN). In this case, it represents the drug which concentration is being studied.

: Patient's own antibodies (ABY) against the drug .

 

1.b) (2 points) Explain how this sensor works

On the absence of antibodies, the potassium ions are able diffuse through the PVC membrane and maintain an ionic current between the two electrolytes. If the patient develops an immune reaction against the drug, then the antibodies will attach to the drug immobilized on the PVC membrane, and reduce the ionic current. In the worst case, the combined AGN-ABY complex would completely block the surface of the membrane and isolate two electrolytic chambers à open circuit. This will be detected by the voltmeter.

1.c) (1 point) Is this a potentiometric or an amperometric sensor? Why?

The particular implementation shown for problem 1 is a potentiometric type sensor since a voltmeter is measuring the potential difference between the two electrodes. If this was a amperometric sensor, then there would be a power supply (e.g. a battery) and a current meter on the circuit.

 

 

2. (4 points) Please draw the photolithographic process steps with annotations to build the MEMS structure shown below:



ANSWER:





 

 

3. (5 points) You are asked to evaluate an accelerometer designed by another engineer as shown below:



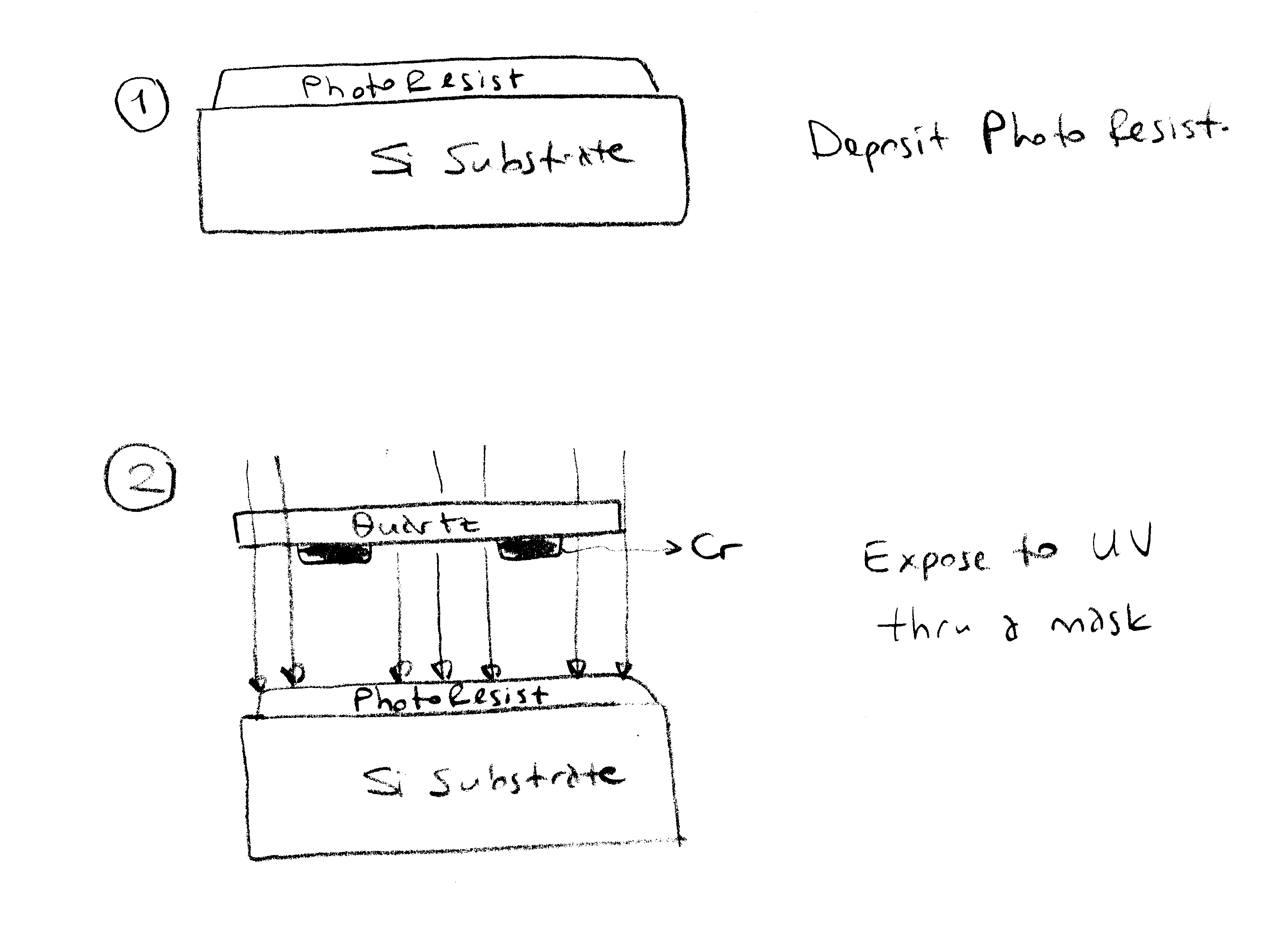
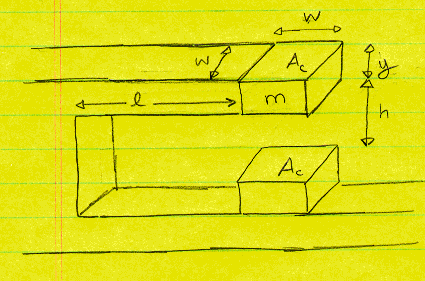
Dimensions are given as follows:

w = 1 mm, ℓ = 100 m m, y = 37 m m, h = 1 m m, A_c is the horizontal surface area

 

Proof Mass is labeled with "m", and is attached to a cantilever beam. Cantilever beam as well as the proof mass is constructed out of Aluminum, which has the following material characteristics:

Density = d = 2.7 grams/cm³, Shear Modulus = G = 26.5 GigaPascals (GPa)

Assume that the proof mass is solid (not flexible), but the cantilever beam is flexible.

If the sensor is exposed to 1 g acceleration (9.81 meters/sec²), how much the distance between the proof mass and square block below it will be? i.e. h - D h. Do you think that is a detectable amount?

 



 

4. (4 points) There are multiple modulation schemes we discussed, one of which was amplitude modulation:
1. (1 point) Explain the main difficulty with amplitude modulation

Amplitude modulation suffers from the problem of signal quality degradation as the distance between the source and transmitter increases. At large distances, amplitude of the received signal is very low. Since the distinction between a "1" and a "0" is the difference in the amplitude of the sinusoidal carrier, at low amplitudes this distinction vanishes, and it becomes very difficult to tell the two codes aparts.

 

2. (2 points) Describe two other modulation schemes (not amplitude modulation)

Frequency Modulation:

Instead of the amplitude of the sinusoidal signal, its frequency is altered according to the data being transmitted. For example, if the carrier frequency is 90 MHz, a zero can be transmitted as 89.99 MHz, and a one can be transmitted as 90.01 MHz.

Pulse Position Modulation:

In this case, only few cycles of the sinusoidal carrier is being used, instead of a continuous sine wave. Furthermore, duration of silent period between the bursts of pulses is adjusted as a function of the transmitted data. For example, to transmit a zero, we can use 1 milli-sec of silence between the pulses, and to transmit a one, we can use 2 milli-sec of silence between the pulses.

 

3. (1 point) Show the modulated signal for data series "101" using the modulation schemes you listed in part 4.2.



5. (4 points) An implantable device is monitoring a patient's blood pressure by taking samples every 90 minutes. During one day, data set shown below was gathered. Show the code assignments for compression of this data using the Hoffman Algorithm.

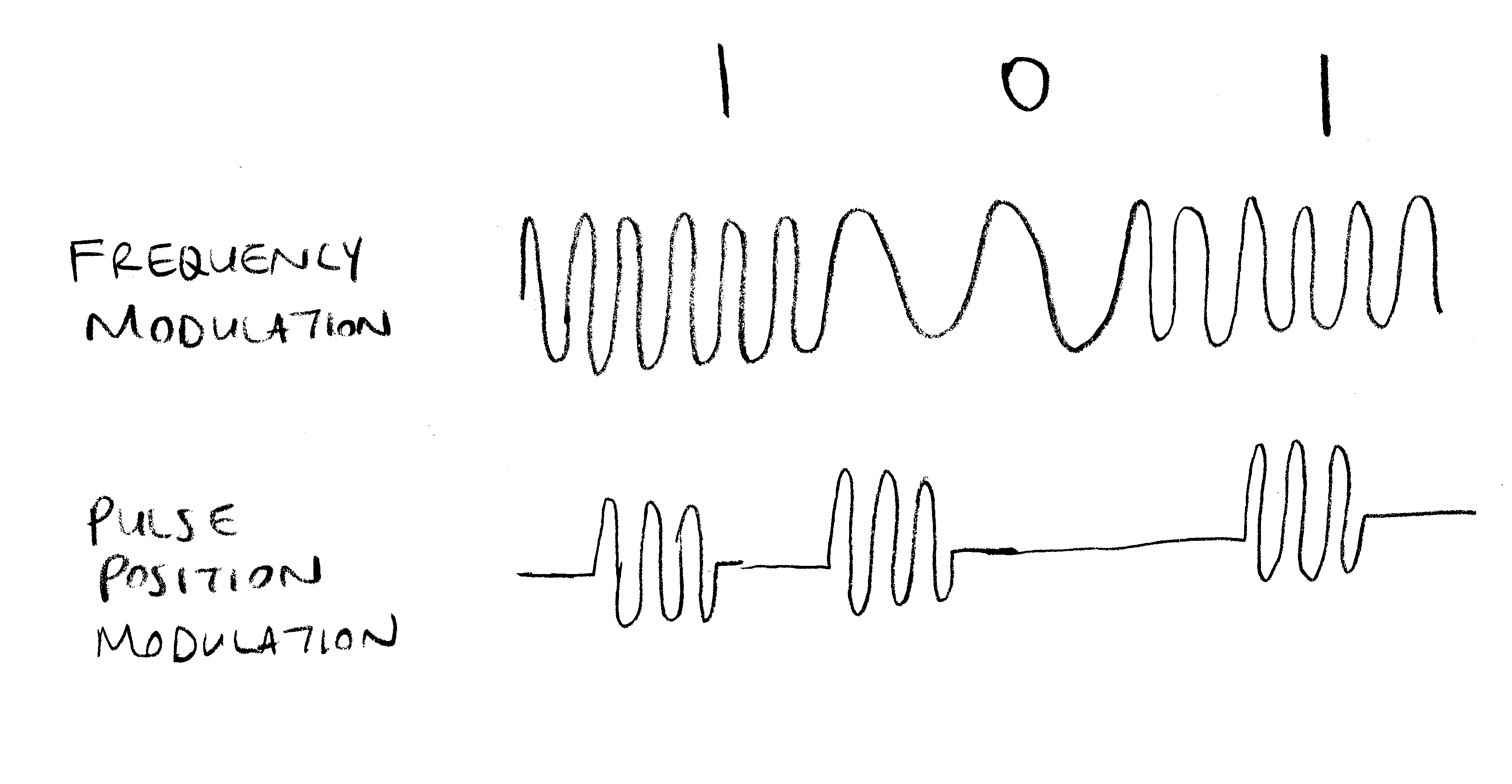
TIME	SYSTOLIC PRESSURE	DIASTOLIC PRESSURE
00:00	140	80
01:30	140	80
03:00	120	80
04:30	120	80
06:00	120	80
07:30	120	80
09:00	160	90
10:30	140	80
12:00	120	80
13:30	160	90
15:00	140	80
16:30	120	80
18:00	120	80
19:30	180	90
21:00	160	90
22:30	140	80

 

ANSWER:

There appears to be only four combinations possible. Lets call them RAW DATA CODEs and use the following table to assign these codes:

RAW DATA CODE - X	SYSTOLIC PRESSURE	DIASTOLIC PRESSURE	N(X)	P(X)
A	140	80	5	5/16
B	120	80	7	7/16
C	160	90	3	3/16
D	180	90	1	1/16

 

Then the raw data looks as follows:

TIME	SYSTOLIC PRESSURE	DIASTOLIC PRESSURE	RAW DATA CODE
00:00	140	80	A
01:30	140	80	A
03:00	120	80	B
04:30	120	80	B
06:00	120	80	B
07:30	120	80	B
09:00	160	90	C
10:30	140	80	A
12:00	120	80	B
13:30	160	90	C
15:00	140	80	A
16:30	120	80	B
18:00	120	80	B
19:30	180	90	D
21:00	160	90	C
22:30	140	80	A

 

Now we can apply the Hoffman algorithm:



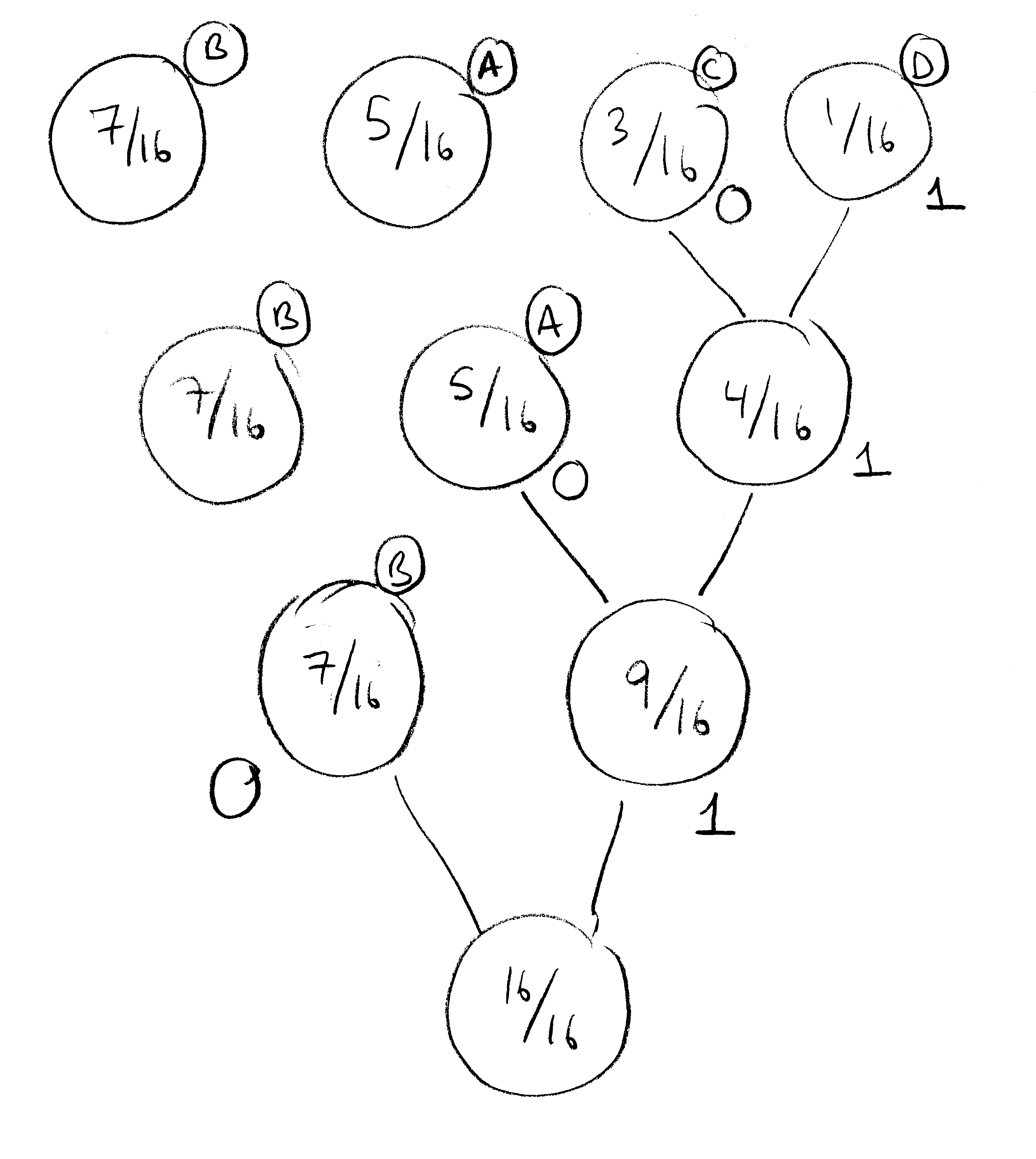
At the end, we will have the following binary code assignments:

RAW DATA CODE - X	SYSTOLIC PRESSURE	DIASTOLIC PRESSURE	BINARY CODE
A	140	80	10
B	120	80	0
C	160	90	110
D	180	90	111

 

 

6. (4 points) Below is a simplified ECG along with a state diagram of a pacemaker. Please fill the table at the back of this page to explain the missing labels: A, B, C, D, E and F.

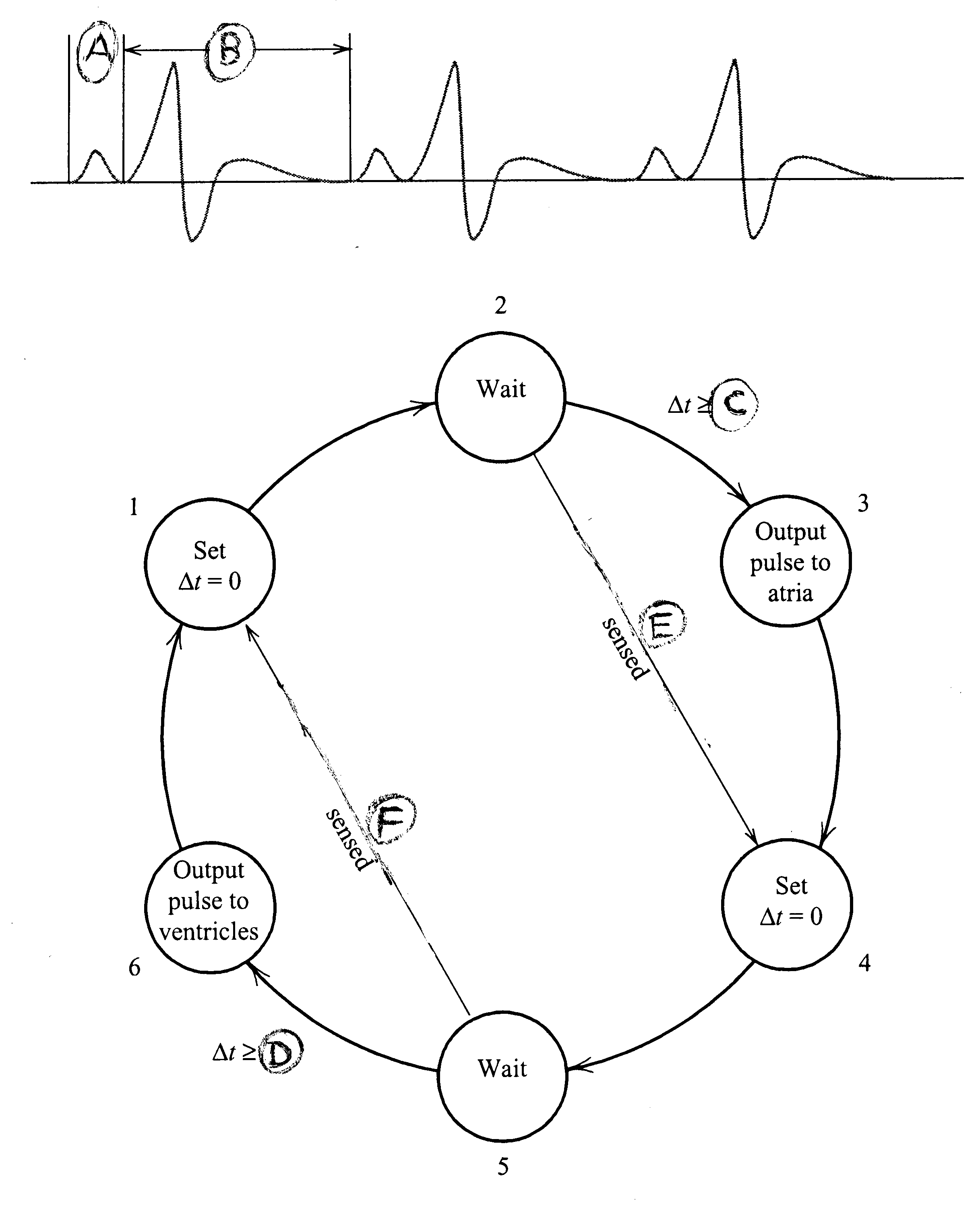
ANSWER: