Distance, Similarity, and Multidimensional Scaling, Self-Organizing Maps
Multidimensional scaling (MDS) is used to map objects into a space based on measures of the (dis)similarity or distance between examples. In other words, MDS is a dimension-reduction algorithm to discover the underlying structure of a space, based on distance measures between objects or cases. The goal is to place observations in a space based on a (dis)similarity scores between them, rather than on features themselves. This seems a little like eigen decomposition, Principal Components Analysis (PCA) or factor analysis, some of which we have already covered and other parts of which we will cover in greater detail later in this course. However, there is one major difference. MDS starts with the similarities, dissimilarities, or distances, while PCA and the like start with a feature representation. Thus, for PCA, you already have everything in a high-dimensional space, and you want to map it into a lower dimensional one. For MDS, you don’t really have a space; just a measure of similarity, and you want to induce the space from that.
For the most part, scaling is used in psychological and perceptual applications, and is a very useful visualization technique. That is, we very often have multiple dimensions we can assess things on, and if we do, MDS is generally a round-about and probably inexact way of doing factor analysis. But in some cases, we can only measure the similarity or distance between examples. In these cases MDS is useful, especially for visualization, identifying significant factors and dimensions. As such, MDS can be used to infer features/dimensions when you don’t have them.
Similarity, Distance and Dissimilarity Measures
The input for MDS is something that behaves like a distance measure between all cases, in the form of a matrix. That is, for N items, you have an NxN matrix where each entry specifies a non-negative distance between items. Mathematically, if we are treating a measure as a distance, we are asserting that our measures have metric properties:
- ``Identity’’. The distance between something and itself is 0. Alternately, two things that have a distance measure of 0 are identical.
- ``Symmetry’’. The distance between A and B is the same as the distance between B and A.
- ``Triangle Inequality’’. The distance between A and C must be less than or equal to the distance between A and B plus the distance between B and C.
These are axioms of distance–assumptions that completely define what a distance is. These place strong constraints on our measures. Many times, we might treat dissimilarity measures as a distance even when it violates one or more of these properties. In fact, most psychological measures will violate at least one of these. These include most direct and indirect measures of similarity. For example, you may directly measure similarity by asking someone to give a rating of the similarity between two objects; or you might infer their similarity by timing how long it takes to choose between them. In the ratings, case, we might not get symmetry–the rating might depend on which option was given first. The RT case we might not get identity–it takes time to identify whether something is the same as itself. Even if we subtract RT for same judgments so that we force the identity property, we might then find that other judgments are faster, and thus negative, which is also a violation of assumptions that distances are positive values.
Although if we had features or a set of numeric predictors, we might use other approaches to map them into smaller dimensions, it is useful to understand how we might map between distance and spatial representation. There are a number of ways to compute distance measures based on numeric features/dimensions. The following are all true distance metrics insofar as they conform to these three axioms, and they are all available within the R dist function (and they are easy to calculate by hand).
Euclidean Distance. This is sometimes referred to as an \(L_2\) norm, and is a generalization of the Pythagorean formula to multiple dimensions. For observations \(a\) and \(b\) measured on many dimensions, this is \(\sqrt{\sum_i((a_i - b_i)^2)}\). Note that even if you use scaling, normalizing, or weighting of dimensions, a distance metric will still result. This is a good default distance measure to use if it makes sense to combine dimensions.
Manhattan or city-block Distance. This is known as the \(L_1\) norm, and is the measure of the sum of the distances along each dimension. For a 2-feature space, it is like walking along streets, rather than as the crow flies. This may be better for categorically distinct features, especially when they are all binary. If they are all binary, this is identical to the Hamming distance–the sum of the differences on each dimension`.
Maximum. This is the largest distance on any one dimensions. This makes sense when the largest difference is the critical predictor. In situations where it doesn’t matter how many aspects match, but rather if there are any big mismatches, this would be a good measure. For many decisions, you might care about worst-case scenarios, and so largest mismatch could be a good measure of how similar you think two cases are.
Asymmetric Binary. Useful for binary feature representations in which presence and absence of a feature is not arbitrary. This measures the proportion of features that mismatch, in which at least one feature is positive. Despite its name, this measure does not violate the symmetry axiom.
Minkowski Distance. This is similar to the ‘softmax’ rule, and is also known as the p norm–the pth root of the sum of the pth powers of the differences of the components. You can specify p, and as p=1, this is the manhattan; as p=2, this is euclidean, as p -> inf this becomes max.
Canberra: This is the absolute difference divided by the sum of the values. This is useful when features are non-negative magnitudes such as counts. \(\sum_i{(|x_i - y_i| / |x_i + y_i|)}\). Terms with zero numerator and denominator are omitted from the sum and treated as if the values were missing.
These are all ways in which a set of features or predictors can be transformed into a distance measure. Oftentimes, you might find that although you have collected dozens or hundreds of features, once you calculate all the pairwise differences, the resulting structure can easily be embedded within a smaller-dimensional space. If so, knowing where the items are within that space can be useful to invert this distance-calculation process.
Although these metrics allow you to go from dimensions to distance, sometimes you may only be able to compute a similarity or distance measure, without knowing the underlying features or dimensions. For example:
- You can judge the similarity of concepts, words, products, ideas, etc., but do not have an easy way of representing their features
- You may have incidental data like mistakes, errors, or discrimination times, that can imply a similarity space, but not a feature space
- In competitive games, you make have good measures of which teams/players are about as good as each other, but not what makes them good.
So, there are many situations in which we may have distance-like measures between pairs of things (similarity or dissimilarity, confusion, etc.). In these cases, we’d sometimes like to be able to reverse the distance formula; getting the coordinates out by putting the distances in. This is what MDS provides solutions for. Before we go into it, let’s consider the differences between similarity and distance.
Similarity versus Distance
Similarity is the opposite of dissimilarity, which is can be interpreted as a distance. However, the notion of dissimilarity does not require satisfying the same metric axioms. For example, similarity/dissimilarity does not need to define what the identity is–what it means to be identical. Similarity measures do not need to be symmetric. Many ways in which similarity is measured produce asymmetric values (see Tversky, 1975). Finally, similarity can violate the triangle inequality. For example, people might agree that North Korea is similar to South Korea, and that North Korea is also similar to Iran, but feel that South Korea and Iran are very different. If these were distances, it would be faster to go from South Korea to Iran through North Korea than directly, which violates spatial axioms implicit in the triangle inequality.
There are many ways of transforming similarities to dissimilarities, and treat them as distances. One way is to subtract from the \(max+\delta\), where \(\delta\) might be 0 if the maximum value is obtained by comparing an item to itself. In general, you may have to add an additive factor to a dissimilarity score for it to work with some of the scaling algorithms we will look at.
Another common way is to use a formula like this: \(distance_j = exp({-\gamma x_j})/\sum_i{exp({ -\gamma x_i})}\). This operates a little like Minkowski distance, where \(\gamma\) will pick out a range of measures between min to mean to max.
simtodist <- function(sims, gamma = 1) {
base <- exp(-gamma * sims)
base/sum(base)
}
print(round(simtodist(c(3, 5, 10, 2, 0), gamma = 1), 3)) ##low similarity becomes large distance[1] 0.042 0.006 0.000 0.114 0.839[1] 0 0 0 0 1[1] 0.200 0.200 0.199 0.200 0.201[1] 0.001 0.007 0.992 0.000 0.000This formula gives us a flexible way of transforming a measure of similarity to a measure of dissimilarity, which might be treated as a distance in an MDS algorithm.
There is a function within the smacof library called
sim2diss, which could be also be used. It has many methods,
but defaults to ‘corr’ which is only appropriate if you have a
correlation matrix, but has about a dozen different principled ways of
creating dissimilarity data from similarity data. The reverse and exp
methods are essentially what we did above, but there are others as well.
Notice that each of these transforms are essentially identical except
for scale, although the d3 is curved, but monotonically related to the
original.
[,1]
[1,] 1.2039728
[2,] 0.6931472
[3,] 0.0000000
[4,] 1.6094379
[5,] 38.3462385Multi-dimensional Scaling
For any set of objects, ideas, concepts, people, etc., we may have a set of pairwise measures that we can interpret as a distance metric–possibly from a high-dimensional set of independent measures (e.g., features or predictors), or with some sort of data that is interpretable directly as a distance. For many types of concepts or objects, we may only be able to make comparisons between pairs, because they may not fall nicely on dimensions. Think about the similarity of words, sounds, paths, shapes, and other complex things. Think about teams in head-to-head competition.
Let’s suppose we knew the only the pairwise distances between locations in a 2-dimensional plane. How might we reconstruct the configuration? This is not too different from how GPS triangulation works. Essentially, we have N*2 values but N^(N-1)/2 data points, and it should be possible to take each triple of points and determine their relative locations, eventually reconstructing the grid. But what if there were errors in measurement, noise, or space had more than two dimensions (or was somehow curved or used a different measure than we are considering? This would be more difficult, because we would never be able to completely trust the location of each point.
In these cases and others, a set of methods called Multi-Dimensional Scaling (MDS) can be thought of as a way of creating a feature-based or spatial representation from similarity data. There are several related algorithms that are used to do this. Simple MDS uses eigen decomposition of the distance measure. More advanced MDS is typically implemented as an iterative process that essentially does triangulation until the points are each in balance in a dimensional space. These are sort of like point connected by springs the size of the measured distance. If there is little error in the distances, everything will align correctly. If there is error, some springs will be under greater tension than others. And if you try to take a 3-dimensional object and compress it by flattening it, you might expect a lot of the springs to be stretched or compressed. The basic amount of stretch the system is under is referred to as ‘stress’ or ‘strain’ in MDS lingo, and is a measure of error. If a high-dimensional system can easily be compressed into a lower-dimensional representation (like layouts of cities on a section of the globe), it will have low stress and be well approximated by a 2-dimensional solution. The stress is also thus a measure of goodness-of-fit, and con be used heuristically to assess how appropriate the solution is.
Classical Metric MDS.
Classical MDS is best applied to metric variables. Torgerson (1958) initially developed this method. It assumes that the data obey distance axioms–they are like a proximity or distance matrix on a map. It uses eigendecomposition of the distance to identify major components and axes, and represents any point as a linear combination of dimensions. Note that this is very similar to PCA or factor analysis, but it uses the distance matrix rather than a correlation matrix as input. Furthermore, its dimensions will be the most important dimensions induced. That is, PCA is able to identify as many dimensions as exist in our original data (up to \(N-1\)), but will retain only the most important ones.
Example: Random points
Look what happens when we choose 6 points on a plane, compute their distances, and then apply cmdscale MDS:
1 2 3 4 5
2 2.318702
3 4.849758 4.399153
4 2.847562 1.209709 3.257179
5 4.076172 1.968488 5.854316 2.685357
6 3.045190 3.318956 1.929530 2.526641 5.158708par(mfrow = c(1, 2))
plot((dummydata), pch = paste(1:6, "", sep = ""), type = "o")
d2 <- cmdscale(dist(dummydata), eig = TRUE)
plot(d2$points, pch = paste(1:6, "", sep = ""), type = "o") Notice that the absolute values are not recovered in terms of the
dimensions or the scale, but the relative positions are. Here the
solution could be rotated, reflected, and it is centered around 0,0.
Next, notice that the x axis has a size of about 9, whereas the y axis
has a size of about 4. This has automatically rotated to the ‘principal’
components.
Notice that the absolute values are not recovered in terms of the
dimensions or the scale, but the relative positions are. Here the
solution could be rotated, reflected, and it is centered around 0,0.
Next, notice that the x axis has a size of about 9, whereas the y axis
has a size of about 4. This has automatically rotated to the ‘principal’
components.
Example: Distances between European Cities
The eurodist data is a matrix of road distances in km between major cities in Europe. We analyze this matrix, specifying that to reproduce the distance based on two dimensions. As a result we can have a two-dimensional representation of the locations of the cities.
Athens Barcelona Brussels Calais Cherbourg Cologne Copenhagen
Barcelona 3313
Brussels 2963 1318
Calais 3175 1326 204
Geneva Gibraltar Hamburg Hook of Holland Lisbon Lyons Madrid
Barcelona
Brussels
Calais
Marseilles Milan Munich Paris Rome Stockholm
Barcelona
Brussels
Calais
[ reached getOption("max.print") -- omitted 17 rows ] [,1] [,2]
Athens 2290.274680 1798.80293
Barcelona -825.382790 546.81148
Brussels 59.183341 -367.08135
Calais -82.845973 -429.91466
Cherbourg -352.499435 -290.90843
Cologne 293.689633 -405.31194
Copenhagen 681.931545 -1108.64478
Geneva -9.423364 240.40600
Gibraltar -2048.449113 642.45854
Hamburg 561.108970 -773.36929
Hook of Holland 164.921799 -549.36704
Lisbon -1935.040811 49.12514
Lyons -226.423236 187.08779
Madrid -1423.353697 305.87513
Marseilles -299.498710 388.80726
Milan 260.878046 416.67381
Munich 587.675679 81.18224
Paris -156.836257 -211.13911
Rome 709.413282 1109.36665
Stockholm 839.445911 -1836.79055
Vienna 911.230500 205.93020
This clearly recreates the geography of Europe, albiet from a strange angle. If you would like the full output, including Goodness-of-fit (GOF); add the ‘eig = TRUE’ statement.
$points
[,1] [,2]
Athens 2290.274680 1798.80293
Barcelona -825.382790 546.81148
Brussels 59.183341 -367.08135
Calais -82.845973 -429.91466
Cherbourg -352.499435 -290.90843
Cologne 293.689633 -405.31194
Copenhagen 681.931545 -1108.64478
Geneva -9.423364 240.40600
Gibraltar -2048.449113 642.45854
Hamburg 561.108970 -773.36929
Hook of Holland 164.921799 -549.36704
Lisbon -1935.040811 49.12514
Lyons -226.423236 187.08779
Madrid -1423.353697 305.87513
Marseilles -299.498710 388.80726
Milan 260.878046 416.67381
Munich 587.675679 81.18224
Paris -156.836257 -211.13911
Rome 709.413282 1109.36665
Stockholm 839.445911 -1836.79055
Vienna 911.230500 205.93020
$eig
[1] 1.953838e+07 1.185656e+07 1.528844e+06 1.118742e+06 7.893472e+05
[6] 5.816552e+05 2.623192e+05 1.925976e+05 1.450845e+05 1.079673e+05
[11] 5.139484e+04 -3.259629e-09 -9.496124e+03 -5.305820e+04 -1.322166e+05
[16] -2.573360e+05 -3.326719e+05 -5.162523e+05 -9.191491e+05 -1.006504e+06
[21] -2.251844e+06
$x
NULL
$ac
[1] 0
$GOF
[1] 0.7537543 0.8679134
The $eig argument gives us how much variance is contributed by each of 21 dimensions the solution produces. We can see that the first two capture almost everything. However, these don’t capture everything, for a couple reasons. First, this was road distances, which means that there will be additional distance for many of the pairs, and these will not be a constant. Second, even if we had exact distances, the curvature of the earth would require at least one extra dimension to incorporate. But nevertheless, a third dimension looks unneccessary.
Assign names (dimension numbers) to the result vectors.
MDS attempts to arrange “objects” (cities) in a space with a particular number of dimensions. As a result of the MDS analysis, we would explain the distances in terms of underlying dimensions. In this case, we could explain distances in terms of the two geographical dimensions:north/south and west east. The axes are not exactly aligned with the cardinal directions (once dim2 is reversed), but it is close. Notice how the general distances are preserved. We can tell that Gibralter to Athens is about 4000 km, and that turns out to be true.
Dim1 <- euro.mds[, 1]
Dim2 <- euro.mds[, 2]
library(ggrepel)
# Plot the solution.
plot(Dim1, -Dim2, type = "n", xlab = "", ylab = "", main = "cmdscale(eurodist)")
text(Dim1, -Dim2, rownames(euro.mds), cex = 0.8)
# Same plot as above; but with different markers and color.
plot(Dim1, -Dim2, xlab = "", ylab = "", main = "cmdscale(eurodist)")
text(Dim1, -Dim2, rownames(euro.mds), cex = 0.8, col = "red")
df <- data.frame(city = rownames(euro.mds), x = euro.mds[, 1], y = euro.mds[, 2])
df |>
ggplot(aes(x = x, y = -y)) + geom_point() + geom_text_repel(aes(label = city)) +
theme_bw()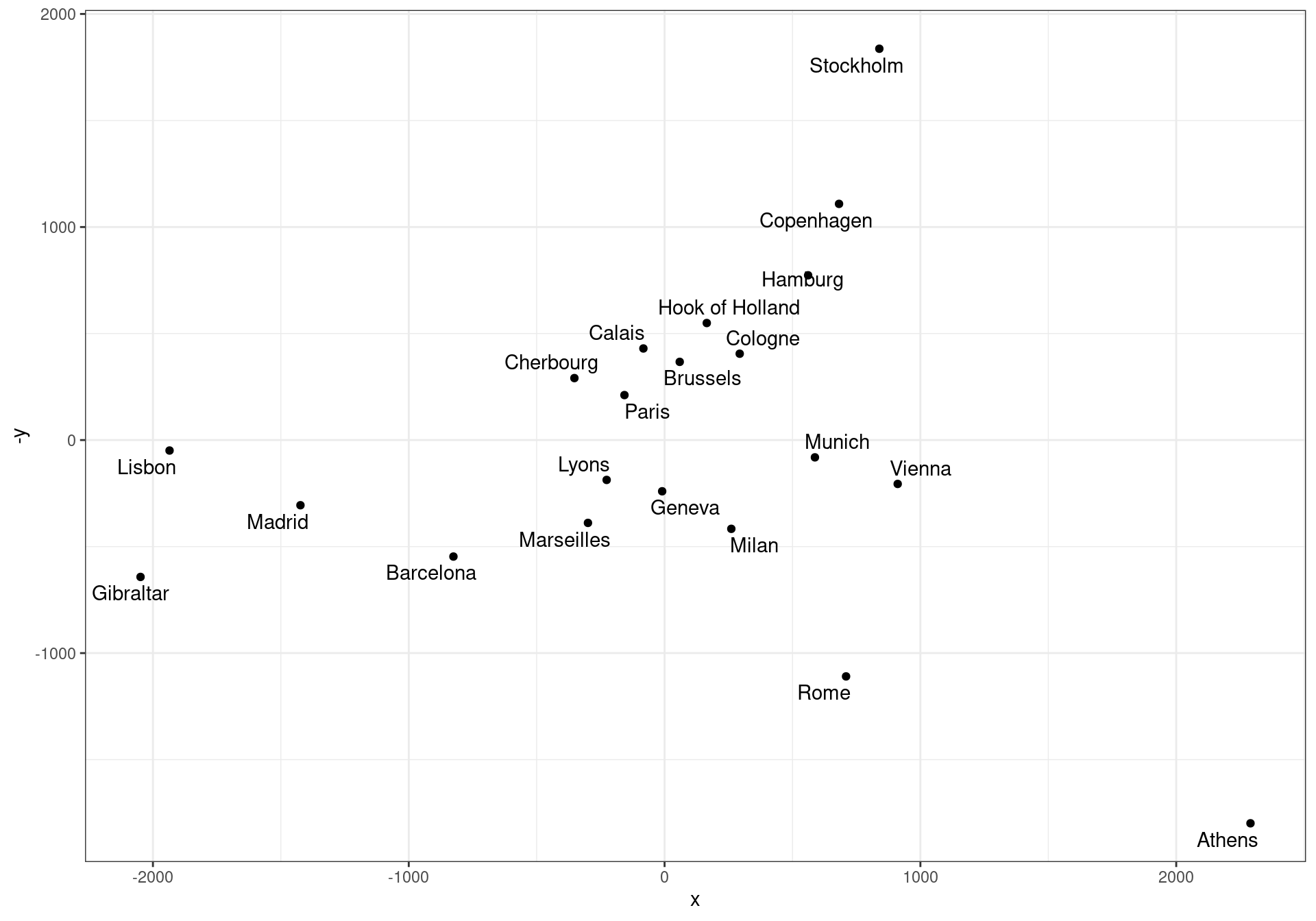
The problem with classic scaling (cmdscale) is that it assumes metric distances, and fits spatial representation to this. This isn’t quite true for even the eurodist data, so we’d like to use methods that make fewer assumptions about the data we have. For example, maybe we think we have error in our measurement, and those errors may be non-linear. Or maybe we can’t count on anything but the ordinal values of our dissimilarity measure. Several methods have been developed to support this.
Sammon’s Non-linear scaling Method
An alternative (non-linear mapping) is the Sammon’s method. Instead
of PCA, it tries to fit the samples into a specified space, and then
adjusts points within that space to find the best configuration. This
chooses (by default) a 2-dimensional configuration based on minimizing
something it calls stress. It uses an underlying notion of the metric
distances, so the exact measure matters, but it permits the weight of
error to be non-linear. This is referred to as non-linear to distinguish
it from things like PCA and the corresponding classic mds
(cmdscale).
In addition, we will look at how we can use this in conjunction with a simple clustering method such as k-means (which we will learn about later in this course), we can use mds as a means for visualizing the clustering.
As an example, we will use the a measure of the dissimilarity between
letters of the alphabet. Then, by applying clustering, we will color
nearby elements the same color. The eqscplot() function in
MASS makes it easy to plot the matrix in the MDS solution.
library(MASS)
distmat0 <- as.matrix(read.csv("plaindist.csv")[, -1])
colnames(distmat0) <- LETTERS
rownames(distmat0) <- LETTERS
plain.dist <- as.dist(distmat0) ##notice as.dist, not dist().
plainsam <- sammon(plain.dist)Initial stress : 0.17463
stress after 10 iters: 0.06485, magic = 0.500
stress after 20 iters: 0.06308, magic = 0.500
stress after 30 iters: 0.06289, magic = 0.500
stress after 40 iters: 0.06286, magic = 0.500$points
[,1] [,2]
A 39.169580 -42.5388560
B 6.885548 11.8850524
C -33.823156 18.7791584
D -12.376599 7.0768170
E 5.225287 -9.2126229
F 10.847292 -19.1335609
G -27.743987 29.4269927
H 20.415393 18.1356304
I -25.457329 -31.2231485
J -35.970132 -1.8001737
K 31.513575 -15.9919172
L -19.972036 -17.6271093
M 59.831861 16.3276882
N 30.005915 10.0410657
O -45.964935 14.7749744
P 12.075377 -0.4255219
Q -29.290945 58.3904347
R 29.418593 -4.3369205
S -11.284700 -4.1844740
T -35.336817 -28.2394601
U -10.031187 19.0979965
V 3.772311 45.6902742
W 40.585080 39.5907235
X 14.053700 -40.8570290
Y -11.920833 -46.9630525
Z -4.626856 -26.6829616
$stress
[1] 0.06286486
$call
sammon(d = plain.dist) [,1] [,2]
A 39.169580 -42.5388560
B 6.885548 11.8850524
C -33.823156 18.7791584
D -12.376599 7.0768170
E 5.225287 -9.2126229
F 10.847292 -19.1335609
G -27.743987 29.4269927
H 20.415393 18.1356304
I -25.457329 -31.2231485
J -35.970132 -1.8001737
K 31.513575 -15.9919172
L -19.972036 -17.6271093
M 59.831861 16.3276882
N 30.005915 10.0410657
O -45.964935 14.7749744
P 12.075377 -0.4255219
Q -29.290945 58.3904347
R 29.418593 -4.3369205
S -11.284700 -4.1844740
T -35.336817 -28.2394601
U -10.031187 19.0979965
V 3.772311 45.6902742
W 40.585080 39.5907235
X 14.053700 -40.8570290
Y -11.920833 -46.9630525
Z -4.626856 -26.6829616[1] 0.06286486
## Clustering will be done next lesson!
k <- kmeans(plain.dist, centers = 5)
eqscplot(plainsam$points, type = "p", cex = 3, pch = 16, main = "Sammon Mapping:\n Letter Similarity with K-Means clustering",
col = k$cluster)
text(plainsam$points, labels = LETTERS, cex = 1.2, col = "white")
df2 <- data.frame(Letter = LETTERS, x = plainsam$points[, 1], y = plainsam$points[,
2], group = as.factor(k$cluster))
df2 |>
ggplot(aes(x = x, y = y, label = Letter, group = group)) + geom_point(size = 8,
aes(color = group)) + geom_text() + theme_bw()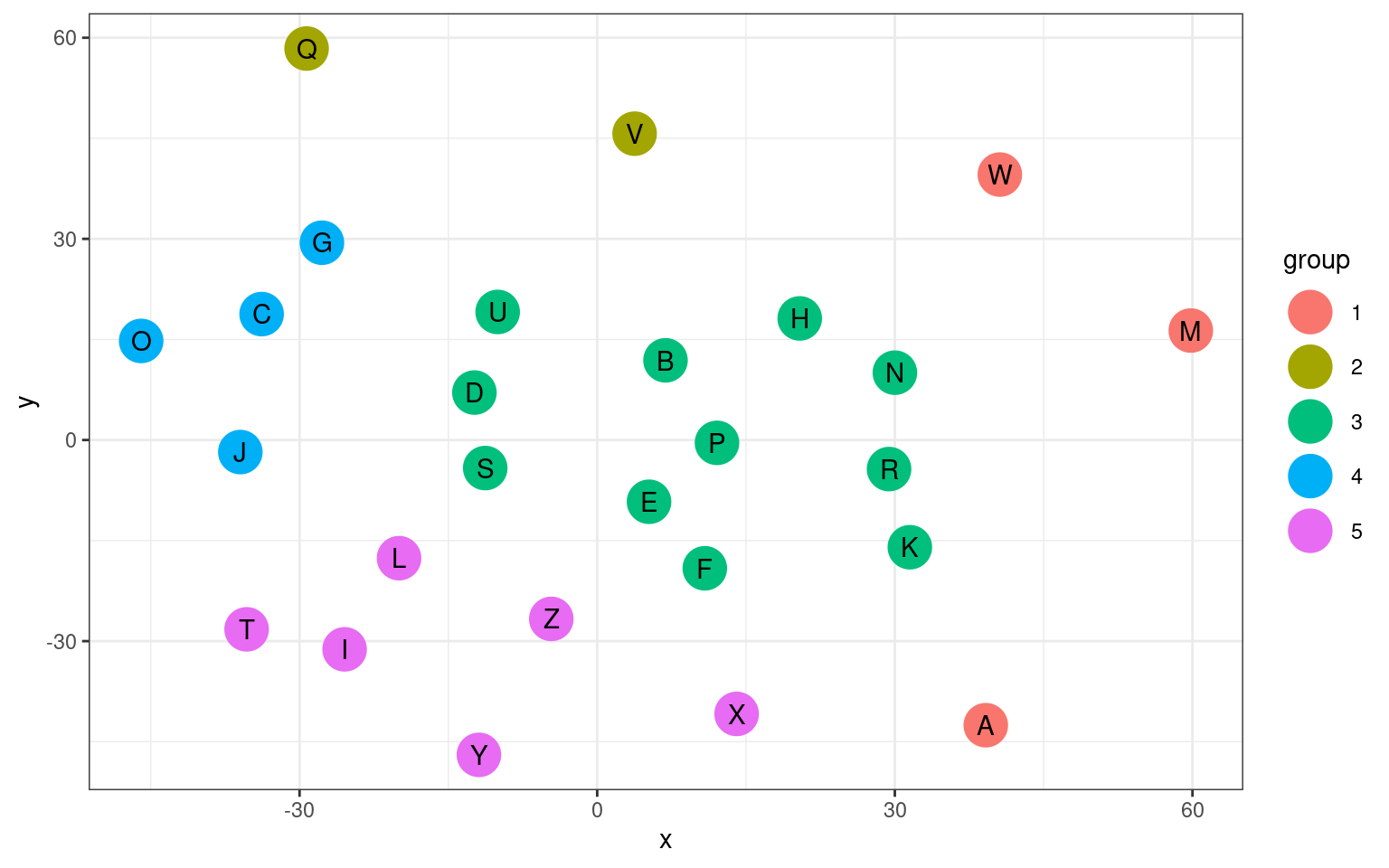
##Non-metric scaling
The assumption that proximities behave like distance might be too restrictive when it comes to employing MDS for exploring the perceptual or subjective similarity spaces of human subjects. Nonmetric MDS, introduced by Kruskal, therefore only assumes that the order of proximities is meaningful. Now, the ‘stress’ scores just count to determine whether the rank order of all the pairwise distances in the solution are the same as the rank order in the similarity. The order of the distances in a nonmetric MDS configuration reflects the order of proximities as good as possible while intervals and ration information is of no relevance. Input data usually are equal interval/ratio variables. This is probably the most famous and widely-used version of MDS.
Here, we will transform our distance matrix into a rank-order matrix, to illustrate how we can use msd on just the rank order points and still recover a reasonable spatial pattern
initial value 7.505733
final value 7.505688
converged

initial value 18.362169
final value 18.352391
convergedpar(mfrow = c(1, 2))
plot(euro.mds2$points, type = "n", main = "MDS from distance")
text(euro.mds2$points, rownames(euro.mds2$points))
plot(euro.mds3$points, type = "n", main = "MDS from rank distance")
text(euro.mds3$points, rownames(euro.mds2$points))
The two spatial mappings above are essentially the same, showing that the isoMDS only uses rank distance. Furthermore, they are quite similar to the metric scaling solution, even though they use non-metric scaling, showing there is a lot of information even in the rank order distances.
Let’s compare isoMDS and cmdscale for the letters: Here is a set of dissimilarity ratings for uppercase letters:
par(mfrow = c(1, 2))
plaindistcmds <- cmdscale(plain.dist)
plot(plaindistcmds, cex = 3, main = "Metric scaling of letters", xaxt = "n", yaxt = "n",
col = "gold", pch = 16, xlab = "", ylab = "")
text(plaindistcmds, LETTERS)
nms <- isoMDS(plain.dist)initial value 27.327755
iter 5 value 20.670653
iter 10 value 18.888452
iter 15 value 18.107814
final value 17.999589
convergedplot(nms$points, cex = 3, main = "Non-metric scaling of letters", xaxt = "n", yaxt = "n",
col = "gold", pch = 16, xlab = "", ylab = "")
text(nms$points[, 1], nms$points[, 2], LETTERS)
There are some small differences between these two spaces, especially the location of A and V.
Determining the number of dimensions in non-metric scaling.
Oftentimes, we use MDS just for visualization, but there are occasions where we are trying to induce features or a space for some other purpose. For example, we might find that a set of concepts needs four dimensions to represent, indicating that some theory that involves only two aspects is insufficient. In these cases, we’d like to determine how many features are needed, and compare the number of dimensions. MDS produces a goodness-of-fit metric called stress, which we can evaluate using a scree plot on the stress.
initial value 43.325635
iter 5 value 35.817503
iter 10 value 34.197372
iter 10 value 34.176392
iter 10 value 34.170116
final value 34.170116
convergedinitial value 26.936929
iter 5 value 20.438842
iter 10 value 19.517270
iter 15 value 18.904334
final value 18.012904
convergedinitial value 20.957449
iter 5 value 14.876172
iter 10 value 14.082124
final value 14.042146
convergedinitial value 12.583692
iter 5 value 10.131807
iter 10 value 9.544001
iter 15 value 9.362428
final value 9.191373
convergedinitial value 10.155951
iter 5 value 7.929799
iter 10 value 7.402915
final value 7.370432
convergedstress = c(mds1$stress, mds2$stress, mds3$stress, mds4$stress, mds5$stress)
dimensions = 1:5
plot(dimensions, stress, type = "b", xlab = "Number of Dimensions", ylab = "Stress") Evaluating these is fairly ad hoc and qualitative. Here, the biggest
jump happens between 1 and 2 dimensions, after which it levels off. But
maybe it is reasonable to use up to 4 dimensions, which would make sense
given the number of features the alphabet has.
Evaluating these is fairly ad hoc and qualitative. Here, the biggest
jump happens between 1 and 2 dimensions, after which it levels off. But
maybe it is reasonable to use up to 4 dimensions, which would make sense
given the number of features the alphabet has.
The smacof library.
The smacof library includes many more advanced tools and
example data sets for MDS. This includes an implementation of
indscal, which handles multiple participants giving
similarity measures, tools for fitting one MDS to another, distance
functions, plotting and fitting algorithms, unfolding analysis,
svm-based MDS, and jacknife/bootstrapping, and other modern tools.
Configurations:
D1 D2
A 0.7301 -0.7128
B 0.1118 0.1995
C -0.6179 0.2889
D -0.2429 0.1084
E 0.0915 -0.1657
F 0.2103 -0.2631
G -0.5514 0.4462
H 0.3704 0.3011
I -0.4333 -0.5707
J -0.6376 -0.0668
K 0.5538 -0.2304
L -0.3307 -0.3597
M 1.0258 0.3703
N 0.5158 0.1944
O -0.7927 0.2325
P 0.2054 0.0174
Q -0.5860 0.9788
R 0.5260 -0.0651
S -0.1647 -0.0556
T -0.5514 -0.5428
U -0.1962 0.3249
V 0.0295 0.8477
W 0.6918 0.7137
X 0.2617 -0.6958
Y -0.1655 -0.8287
Z -0.0537 -0.4663
Stress per point (in %):
A B C D E F G H I J K L M N O P
6.94 2.78 3.41 2.96 1.62 4.19 4.35 2.40 2.14 3.68 2.15 4.65 5.17 3.41 3.94 4.21
Q R S T U V W X Y Z
3.70 2.00 4.80 3.12 2.62 8.51 3.96 4.08 5.45 3.77 Here, we see that a number of different mds option are available, and we get a per-item stress score.
The plotting functions will plot the object, unlike isoMDS which had no plotting methods.




 # Example: Country data
# Example: Country data
These are ratings of similarity across several countries, from Kruskal’s original monograph. There are one or more errors in this. Can you identify what is wrong, and how we can fix it?
countries <- c("Brazil", "Congo", "Cuba", "Egypt", "France", "India", "Israel", "Japan",
"China", "Russia", "USA", "Yugoslavia")
sims <- c(4.83, 5.28, 4.56, 3.44, 5, 5.17, 4.72, 4, 4.11, 4.78, 4.5, 4.83, 4, 5.83,
3.44, 3.83, 3.33, 3.61, 4.67, 4, 4.11, 3.5, 3.39, 2.94, 3.83, 4.22, 4.5, 4.83,
2.39, 4, 5.5, 4.39, 3.67, 4.11, 3, 4.17, 3.06, 3.39, 5.44, 4.39, 5.06, 4.5, 4.17,
4.61, 5.72, 5.39, 2.39, 3.17, 3.33, 5.94, 4.28, 5.94, 6.06, 2.56, 5, 3.17, 3.5,
5.11, 4.28, 4.72, 4, 4.44, 4.28, 5.06, 6.67, 3.56)
cdist <- matrix(0, nrow = length(countries), ncol = length(countries))
cdist[upper.tri(cdist)] <- max(sims) - sims + 0.01
colnames(cdist) <- countries
rownames(cdist) <- countries
cdist Brazil Congo Cuba Egypt France India Israel Japan China Russia USA
Brazil 0 1.85 1.40 3.24 1.96 2.18 2.85 3.18 4.29 3.62 1.29
Congo 0 0.00 2.12 1.68 2.68 1.85 3.35 3.29 2.68 3.29 4.29
Cuba 0 0.00 0.00 1.51 2.57 2.68 3.07 3.74 1.18 1.24 3.51
Egypt 0 0.00 0.00 0.00 1.90 0.85 2.01 2.85 2.29 2.29 3.35
France 0 0.00 0.00 0.00 0.00 3.24 2.68 2.46 3.01 1.62 0.74
India 0 0.00 0.00 0.00 0.00 0.00 2.57 2.18 2.57 2.18 2.40
Yugoslavia
Brazil 3.51
Congo 3.18
Cuba 1.57
Egypt 2.40
France 1.96
India 2.68
[ reached getOption("max.print") -- omitted 6 rows ]initial value 45.276620
iter 5 value 30.016227
iter 10 value 25.742007
final value 25.407874
converged
(hint: Which two countries are the most similar? The least?)
Example: Michigan Politics
Let’s consider the voting patterns of of Michigan lawmakers. We can use the voting patterns to compute a similarity metric, and then use MDS to place the politicians in a political space.
library(MASS)
senate <- read.csv("misenate.csv")
votes <- senate[, -(1:2)]
rownames(votes) <- paste(senate$X, senate$Party)
sdistance <- dist(votes, method = "manhattan")
sum(is.na(sdistance))[1] 11Notice that we have 11 NA cases here, probably because of missing data. We have several people with many NA values, including #22, 60, 62, 98, 107, and 112. Let’s remove them and try again:
senate <- senate[-c(22, 60, 62, 98, 107, 112), ]
votes <- senate[, -(1:2)]
rownames(votes) <- paste(senate$X, senate$Party)
sendist <- dist(votes, method = "manhattan")
sum(is.na(sendist))[1] 0Now, we are in good shape. (Some of these algorithms won’t work well with missing values). However, this fails, warning us that we have zero distance between two objects:

nsen <- nrow(sendist)
## add a little noise because sammon complains about identical cases.
nsdistance <- as.matrix(sendist) + 0.01 + matrix(runif(nsen * nsen) * 0.01, nsen)
# d2 <- isoMDS(sdistance,k=2) #this fails! d2 table(sdistance) not run: causes
# an error isoMDS(sdistance,k=2) Error in isoMDS(sdistance, k = 2) : zero or
# negative distance between objects 22 and 27In fact, there are five pairings that have distance 0. These show up as white squares in the image plot. In our case, this happens because we have two individuals who voted the same on every issue. The problem is that MDS can have problems with this. If the distance between two things is the same, then they are the same thing, so it doesn’t make sense to have separate things that are the same. In these cases, there are ties in rank order, and the like. We can fix this by just adding a small positive value to every distance. Thus, no two individuals will be exactly identical, and the algorithm works fine. Let’s try looking at 2,3, and 4-dimensional solutions:
initial value 11.379776
iter 5 value 9.138091
iter 10 value 8.186514
final value 8.021785
convergedinitial value 9.884424
iter 5 value 7.437103
iter 10 value 6.561058
final value 6.333007
convergedinitial value 9.138676
iter 5 value 6.726061
iter 10 value 5.843012
iter 15 value 5.588703
iter 20 value 5.452384
iter 20 value 5.447255
iter 20 value 5.444646
final value 5.444646
convergedThe stress is substantially reduced by moving to 3 dimensions, but then it does not improve much. This might suggest a 3-dimensional solution can describe the political landscape of Michigan politicians. 3-dimensional is difficult to visualize, so let’s start with the 2-D solution:
library(ggplot2)
dat <- data.frame(d2$points)
dat$name <- rownames(dat)
dat$party <- senate$Party
colnames(dat) <- c("x", "y", "name", "party")
ggplot(dat, aes(x = x, y = y, col = party)) + geom_point() + theme_bw()
This suggests that although republicans and democrats cluster together and separate well, there is at least one additional dimension that divides members within each party. If we knew more about issues, members, geography, and voting patterns, we might be able to label this second axis. It would also be useful to look at the 3rd dimension.
dat <- data.frame(d3$points)
dat$name <- rownames(dat)
dat$party <- senate$Party
colnames(dat) <- c("x", "y", "z", "name", "party")
ggplot(dat, aes(x = x, y = y, col = party)) + geom_point() + theme_bw()

Non-linear Sammon scaling will also give a solution (and this also fails if the min distance is 0). Notice that this tends to space individual points out a bit more.
Initial stress : 0.04199
stress after 10 iters: 0.02620, magic = 0.018
stress after 20 iters: 0.02225, magic = 0.150
stress after 30 iters: 0.02178, magic = 0.346
stress after 40 iters: 0.02106, magic = 0.500
stress after 50 iters: 0.02092, magic = 0.500
stress after 60 iters: 0.02088, magic = 0.500dat2 <- dat
dat2$x <- s2$points[, 1]
dat2$y <- s2$points[, 2]
ggplot(dat2, aes(x = x, y = y, col = party)) + geom_point() + theme_bw()
Boundary Conditions
What if we really don’t have a good metric structure? These algorithms will still work, but what will they tell us? Let’s choose a set of random pairwise distances for 50 points. Play with different values for min and noise to see how the resulting space looks:
min <- 10
noise <- 0.1
n <- 100
distance <- matrix(runif(n * n) * noise + min, n, n)
distance <- (distance + t(distance))/2
diag(distance) <- 0
par(mfrow = c(1, 2))
m <- cmdscale(distance, k = 2)
plot(m, main = "Classic scaling")
m2 <- isoMDS(distance, k = 2)initial value 43.586888
final value 39.913807
converged Oftentimes, the result will form a ring or circle. Although this is
sometimes an indication of what the space is like, it is also a marker
for a similarity space that does not fit into a metric space well. If
everything in the space is equally distant to everything else, the best
way to map that into a 2-dimensional space is as a circle.
Oftentimes, the result will form a ring or circle. Although this is
sometimes an indication of what the space is like, it is also a marker
for a similarity space that does not fit into a metric space well. If
everything in the space is equally distant to everything else, the best
way to map that into a 2-dimensional space is as a circle.
Correlation as distance and the Personality Circumplex
Correlation is not a distance, but 2-cor(x) or 1- abs(cor(x)) might be reasonable. Now, identical things will have a measure of 0, and independent things or completely negatively correlated things will have a measure of 1.0.
big5 <- read.csv("bigfive.csv")[, -1]
qtype <- as.factor(c("E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "E", "A",
"C", "N", "O", "E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "E", "A", "C",
"N", "O", "E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "O", "A", "C", "O"))
cb <- cor(big5, use = "pairwise.complete")
d1 <- 1 - abs(cb)
d2 <- 2 - cb
m1 <- isoMDS(d1, k = 2)initial value 36.251113
iter 5 value 28.318084
final value 27.626587
convergedinitial value 28.107205
iter 5 value 20.942080
iter 10 value 20.252167
iter 10 value 20.236860
iter 10 value 20.229681
final value 20.229681
convergedpar(mfrow = c(1, 2))
plot(m1$points, col = qtype, pch = 16, cex = 3, main = "Personality trajectories")
text(m1$points[, 1], m1$points[, 2], qtype, col = "white")
plot(m2$points, col = qtype, pch = 16, cex = 3, main = "Personality dimensions")
text(m2$points[, 1], m2$points[, 2], qtype, col = "white")
Like with the random points, we see a circumplex here, probably indicating we have more than two dimensions. But depending on the approach, we see like questions clustering along axes or within common areas of space. The different personality dimensions cluster together, allowing some validation of the method. You could also score every person by how they answered questions to put them somewhere within this space.
Self-organizing maps or Kohenen maps
Another crude approach to scaling is what is known as the self-organizing map of Kohonen. This is a bit different from scaling, as it starts with the assumption that your cases are on a grid or lattice (a map), and then has the individual cases organize themselves by moving around the map until you get a stable solution. To visualize this, we will create little radial plots for each case so you can visualize them. We need to specify a grid that is no larger than the number of cases as well. There are 112 Michigan senators, which is 8 * 14, so that will work. If we specify a smaller number, multiple individuals will be placed on a single point in the grid.
library(class)
votes2 <- votes
votes2[is.na(votes2)] <- 0.5
rn <- rownames(votes)
party <- substr(rn, nchar(rn), nchar(rn))
gr <- somgrid(topo = "hex", xdim = 10, ydim = 10)
b <- SOM(votes2, gr, 1:54/54)
plot(b)
points(b$grid$pts[, 1], b$grid$pts[, 2], pch = 16, col = "white", cex = 2)
text(b$grid$pts[, 1], b$grid$pts[, 2], party, cex = 0.75, col = c("red", "blue")[(party ==
"D") + 1]) This looks to group like things together, but for SOMs with have to
worry about initial configuration. Note that the cases are already
organized by party, so that might put them in a good starting
configuration. Let’s shuffle and try again.
This looks to group like things together, but for SOMs with have to
worry about initial configuration. Note that the cases are already
organized by party, so that might put them in a good starting
configuration. Let’s shuffle and try again.
library(class)
ord <- order(runif(nrow(votes)))
votes2 <- votes[ord, ]
votes2[is.na(votes2)] <- 0.5
rn <- rownames(votes)
party <- substr(rn, nchar(rn), nchar(rn))
gr <- somgrid(topo = "hex", xdim = 10, ydim = 10)
b <- SOM(votes2, gr, 1:54/54)
plot(b)
points(b$grid$pts[, 1], b$grid$pts[, 2], pch = 16, col = "white", cex = 2)
text(b$grid$pts[, 1], b$grid$pts[, 2], party, cex = 0.75, col = c("red", "blue")[(party ==
"D") + 1])
This seems to do about as well. This approach starts with features and ends with a 2D map, which is sort of like what PCA does. If you only have similarity data to start with, you might have to be creative to make it work, but it focuses on local similarities rather than the overall space, and is a handy alternative to scaling algorithms.
A Comparative example
Suppose we create a grid of 16 points in 2d Space, and measure distance but add a little noise to make it interesting:
library(ggplot2)
ord <- order(runif(16))
x <- rep(1:4, each = 4)[ord]
y <- rep(1:4, 4)[ord]
label <- paste(LETTERS[1:4][x], LETTERS[1:4][y], sep = "-")
xydistance <- dist(cbind(x, y)) + abs(rnorm(120))
data.frame(x, y, label) |>
ggplot(aes(x = x, y = y)) + geom_point(size = 13) + geom_text(aes(label = label),
color = "white") + theme_bw()
PCA and variable reduction
We earlier learned about PCA via eigen decomposition. Suppose we just treat the distances as features and do an eigen decomposition:
e <- eigen(xydistance)
data.frame(x = e$vectors[, 1], y = e$vectors[, 2], labels = label, xgroup = factor(x),
ygroup = factor(y)) |>
ggplot(aes(x = x, y = y, group = xgroup, color = xgroup)) + geom_line() + geom_point(size = 13) +
geom_text(aes(label = label), color = "white") + theme_bw() + ggtitle("Eigen decomposition of distance matrix")
This does not really recover the space very well
Classical scaling
The classical scaling approach does a great job of recovering the grid shape.
cmds <- cmdscale(xydistance)
data.frame(x = cmds[, 1], y = cmds[, 2], labels = label, xgroup = factor(x), ygroup = factor(y)) |>
ggplot(aes(x = x, y = y, group = xgroup, color = xgroup)) + geom_line() + geom_point(size = 13) +
geom_text(aes(label = label), color = "white") + theme_bw() + ggtitle("Classic MDS (cmdscale)")
This produces a rotation, and the basic layout is reasonable, but a bit wobbly.
Sammon mapping
Initial stress : 0.05488
stress after 10 iters: 0.03790, magic = 0.092
stress after 20 iters: 0.03139, magic = 0.500
stress after 30 iters: 0.03138, magic = 0.500data.frame(x = sam$points[, 1], y = sam$points[, 2], labels = label, xgroup = factor(x),
ygroup = factor(y)) |>
ggplot(aes(x = x, y = y, group = xgroup, color = xgroup)) + geom_line() + geom_point(size = 13) +
geom_text(aes(label = label), color = "white") + theme_bw() + ggtitle("Sammon scaling")
Non-metric mapping
initial value 16.901956
final value 13.414387
convergeddata.frame(x = iso$points[, 1], y = iso$points[, 2], labels = label, xgroup = factor(x),
ygroup = factor(y)) |>
ggplot(aes(x = x, y = y, group = xgroup, color = xgroup)) + geom_line() + geom_point(size = 13) +
geom_text(aes(label = label), color = "white") + theme_bw() + ggtitle("Non-metric (isoMDS) scaling") The sammon and isoMDS have much more regular outcomes, because the
rank-order distance erases some of the noisiness.
The sammon and isoMDS have much more regular outcomes, because the
rank-order distance erases some of the noisiness.
Self-organizing maps
library(class)
gr <- somgrid(topo = "rectangular", xdim = 4, ydim = 4)
b <- SOM(as.matrix(xydistance), gr, radii = 100:1/10, alpha = 100:1/5)
plot(b)

data.frame(x = b$grid$pts[, 1], y = b$grid$pts[, 2], labels = label, xgroup = factor(x),
ygroup = factor(y)) |>
ggplot(aes(x = x, y = y, group = xgroup, color = xgroup)) + geom_line() + geom_point(size = 13) +
geom_text(aes(label = label), color = "white") + theme_bw() + ggtitle("Self-organizing map (SOM)") The SOM does well sometimes, but its accuracy is a bit deceptive,
because it assumes the points lie on a grid, and then finds a good
organization of the cases in that grid. It tends to get stuck in
reasonable but suboptimal configurations.
The SOM does well sometimes, but its accuracy is a bit deceptive,
because it assumes the points lie on a grid, and then finds a good
organization of the cases in that grid. It tends to get stuck in
reasonable but suboptimal configurations.