Clustering Methods
Additional Reading: Venables & Ripley MASS Chapter 11
This unit covers a handful of clustering approaches, including k-means clustering, a number of hierarchical clustering approaches (divisive and agglomerative), and variations on these methods.
Clustering Approaches
Previously, we examined MDS, that attempted to find a coordinate system to map items into based on their (dis)similarity. Sometimes this revealed fuzzy groups, and other times just dimensions in space that were sometimes interpretable. During the unit on machine classification, we covered partitioning approaches that tried to find ways of grouping data together based on simple decision rules to best predict a specific category. What happens if you don’t know the identity, but still want to come up with bottom-up categories? We can use a distance metric to identify groups without knowing their labels–a general approach called clustering.
Just like MDS, clustering approaches find ways of grouping data together based on implied dissimilarity, which can sometimes be interpreted as ‘distance’. We assume that we have either measured or can compute a dissimilarity score (akin to a distance) for every pair of items. If we have this dissimilarity measure or can transform our measure to be a dissimilarity measure, these approaches are feasible. Interestingly, when we were covering MDS, we said that if you have a feature based representation, you might use PCA directly instead of transforming feature coding into a similarity space and then re-inducing a metric space from that similarity space. For most of the clustering methods we will consider in this unit, we similarly need a distance space, and end up computing one and throwing out the initial feature representation. This is not universally true for all clustering methods (e.g., finite mixture modeling does not do this), but it is an assumption clustering approaches make that inferred distance measures are an accurate depiction of the similarity space.
Psychological Distance
Many times, similarity ratings and behavioral measures (errors or response time) are treated as a indexing a psychological distance. However, this analogy is often mistaken and misleading, as argued by Tversky (1975). Most examples of subjective similarity (or dissimilarity) violate one or another of the axioms of metric spaces, which say that (1; identity) The distance between something and itself is 0; (2. symmetry) the distance between A and B is the same as the distance between B and A; and (3. triangle inequality) the D(A,B) + D(B,C)> D(A,C). This last one is hard to satisfy in subjective similarity: frosted flakes are similar to cheerios, and cheerios are similar to bagels, but frosted flakes are not similar to bagels. This means that for ratings such as this, distance is the wrong metaphor to use to understand what is going on, and maybe that scaling approaches (to be covered later) and factor analytic approaches are flawed as well, as they assume metric properties that might not exist.
Basic Approaches to clustering
If you have the goal of developing a clustering solution, there are two basic approaches (and hybrids between them). On one side, you could start with the notion of making a complete hierarchical description of all the elements. This is like a complete partitioning tree, where every element ends up being a leaf in the tree. The tree can then be examined for structure, or potentially chopped off to reveal the most important clusters. Everything is in multiple clusters of different levels. These methods are called ```hierarchical clustering’’’ methods. On the other hand, you might start with an assumption that there are a fixed number of groups. Based on that assumption, you may try to find the best arrangement of elements into clusters that fits your assumptions. This might be called a finite clustering method, and is typified by k-means clustering and related techniques. There are hybrids, especially within Bayesian approaches, that permit an infinite number of groups, and different optimization/inference approaches, including Bayesian inference and E-M optimization. The traditional approaches use distance measures directly, and include both agglomerative and divisive approaches to hierarchical clustering and k-means and related methods for finite clustering.
Hierarchical Clustering
Tversky made several suggestions to account for the findings, based primarily on the fact that different features are weighted differently. This seems to favor an approach where data can be partitioned based on dissimilarity of one feature, such that if two things differ on an important feature, matches along less important features might not matter. He suggested a hierarchical clustering approach to characterize data of this sort.
In a hierarchical approach, you create a binary tree, so that the first split divides the population into two groups that are most different, and each sub-population is split, recursively, until everything is on its own leaf. There are a number of ways to do this, but the final solution provides a complete set of dissimilarity measures that are ‘’ultra-metric’’ when visualized in a tree. The dissimilarity between any two elements is interpreted as the measure of the largest group that contains both items. Note that we throw away the complete dissimilarity matrix and replace it with one inferred by the cluster. Sometimes this works and we have a useful representation.
Sample Data: Alphabet Similarity
The example below uses the response time data to different letter pairs as an example.
distmat0 <- as.matrix(read.csv("plaindist.csv")[, -1])
colnames(distmat0) <- LETTERS
rownames(distmat0) <- LETTERS
distmat0[1:5, 1:5] A B C D E
A 0.00000 61.10980 76.51373 61.25098 60.34510
B 61.10980 0.00000 50.77647 28.70588 23.72941
C 76.51373 50.77647 0.00000 46.55686 44.63922
D 61.25098 28.70588 46.55686 0.00000 34.51373
E 60.34510 23.72941 44.63922 34.51373 0.00000## Transform it into distance matrix
distmat <- as.dist(distmat0)
image(1:26, 1:26, distmat0, xaxt = "n", yaxt = "n", main = "Similarity of letters",
xlab = "", ylab = "")
axis(1, 1:26, LETTERS, cex.axis = 0.75)
axis(2, 1:26, LETTERS, cex.axis = 0.75)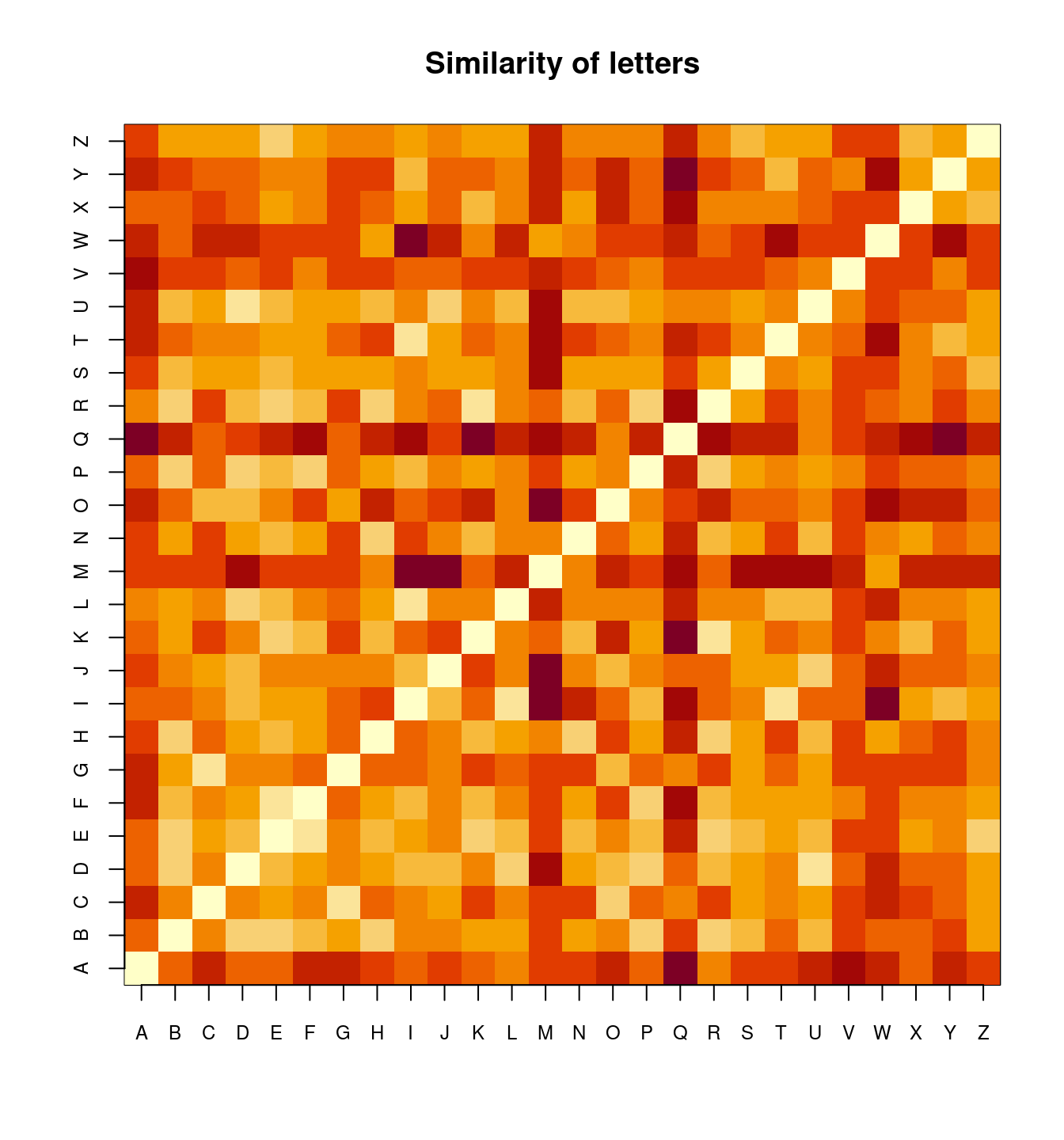
Along with the subjective similarity rating data, we can often give clustering algorithms feature or dimensional data. For comparison, we will look at a feature-level analysis of letters produced by Keren & Baggen (1981). Here, the features include things like roundness, horizontal, vertical features, and the like.
V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15
A 0 0 1 1 1 0 0 1 0 0 0 1 0 0
B 1 1 0 1 1 0 0 0 1 0 1 0 0 0
C 1 0 0 0 0 0 0 0 1 0 1 0 0 1
D 1 1 0 0 0 0 0 0 1 0 1 0 0 0
E 1 0 0 1 0 0 0 0 0 0 1 0 0 1
[ reached 'max' / getOption("max.print") -- omitted 21 rows ]Notice that distmat has been pre-processed and scaled to produce a distance-like measure. The diagonal is always 0, but what else shows up? It is hard to say for sure. We could apply and MDS like before to understand the space.
initial value 27.327755
iter 5 value 20.670653
iter 10 value 18.888452
iter 15 value 18.107814
final value 17.999589
converged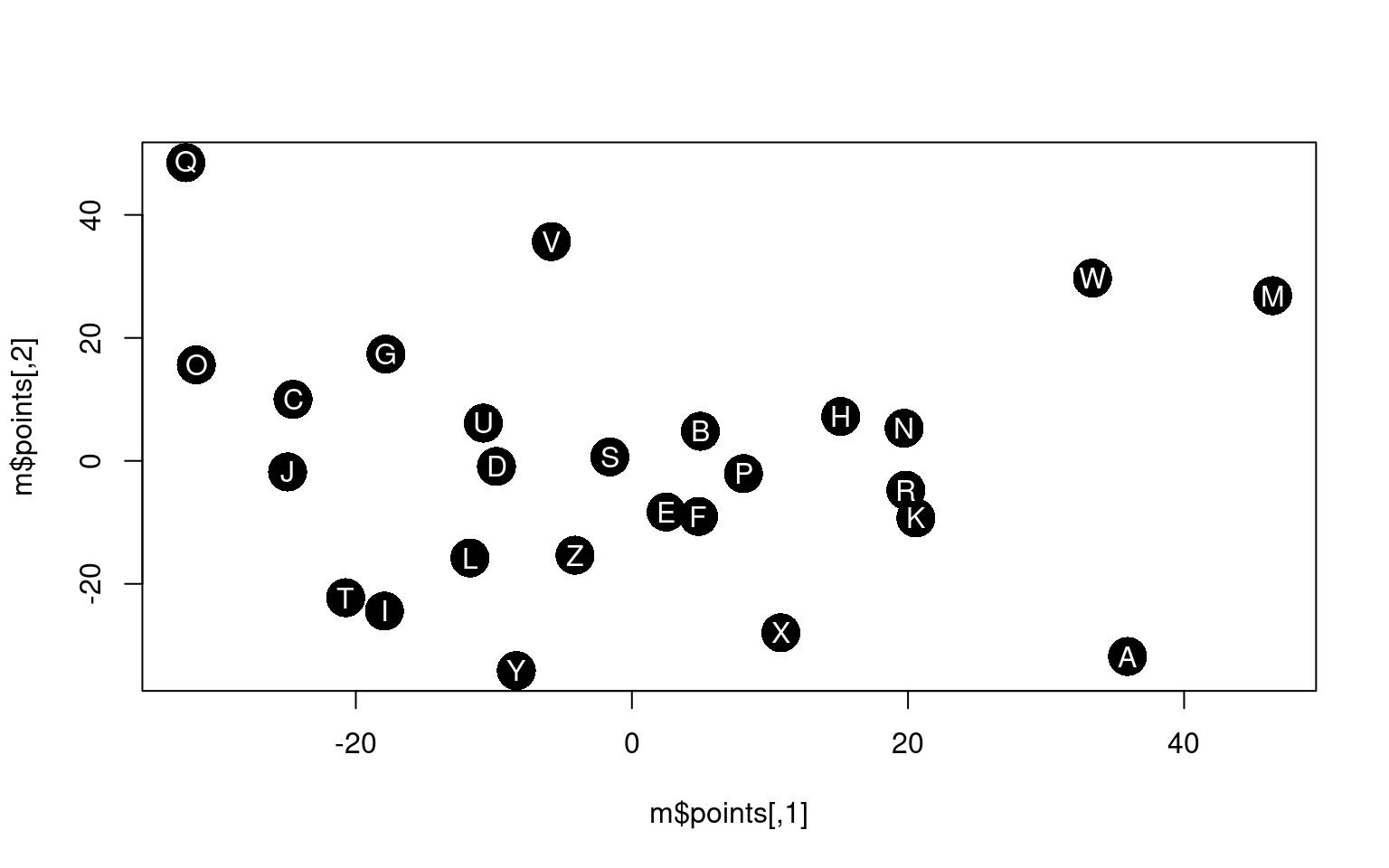 The MDS puts similarly-shaped letters in similar positions. However, a
clustering approach may show other things. First, we will consider
hierarchical clustering methods. Hierarchical clustering attempts to
find a hierarchy that groups or divides items repeatedly until the whole
set is characterized by a binary tree. In order to do this, we need to
decide on whether we want to start from the bottom (called
agglomerative), merging pairs together, then adding groups together,
until the entire data set is merged, or start at the top (called
divisive), repeatedly dividing sets in ways that maximize within-set
similarity and minimize between-set similarity. Once we decide on the
direction, we also needs to determine a method for defining what ‘close’
means when we want to divide or merge items and clusters. For example,
do we count the similarity of two groups to be the largest of the
inter-cluster similarity, the smallest, the average, or something else.
We will start by examining the clustering methods in the \(cluster\) library.
The MDS puts similarly-shaped letters in similar positions. However, a
clustering approach may show other things. First, we will consider
hierarchical clustering methods. Hierarchical clustering attempts to
find a hierarchy that groups or divides items repeatedly until the whole
set is characterized by a binary tree. In order to do this, we need to
decide on whether we want to start from the bottom (called
agglomerative), merging pairs together, then adding groups together,
until the entire data set is merged, or start at the top (called
divisive), repeatedly dividing sets in ways that maximize within-set
similarity and minimize between-set similarity. Once we decide on the
direction, we also needs to determine a method for defining what ‘close’
means when we want to divide or merge items and clusters. For example,
do we count the similarity of two groups to be the largest of the
inter-cluster similarity, the smallest, the average, or something else.
We will start by examining the clustering methods in the \(cluster\) library.
The cluster library
Several clustering methods are available within the
cluster library. A hierarchical clustering might look like
this. We will start with agnes, an agglomerative clustering
approach. This is bottom-up, and finds the closest pairs at each stage
to link together, linking items and existing clusters together until the
entire set is linked.
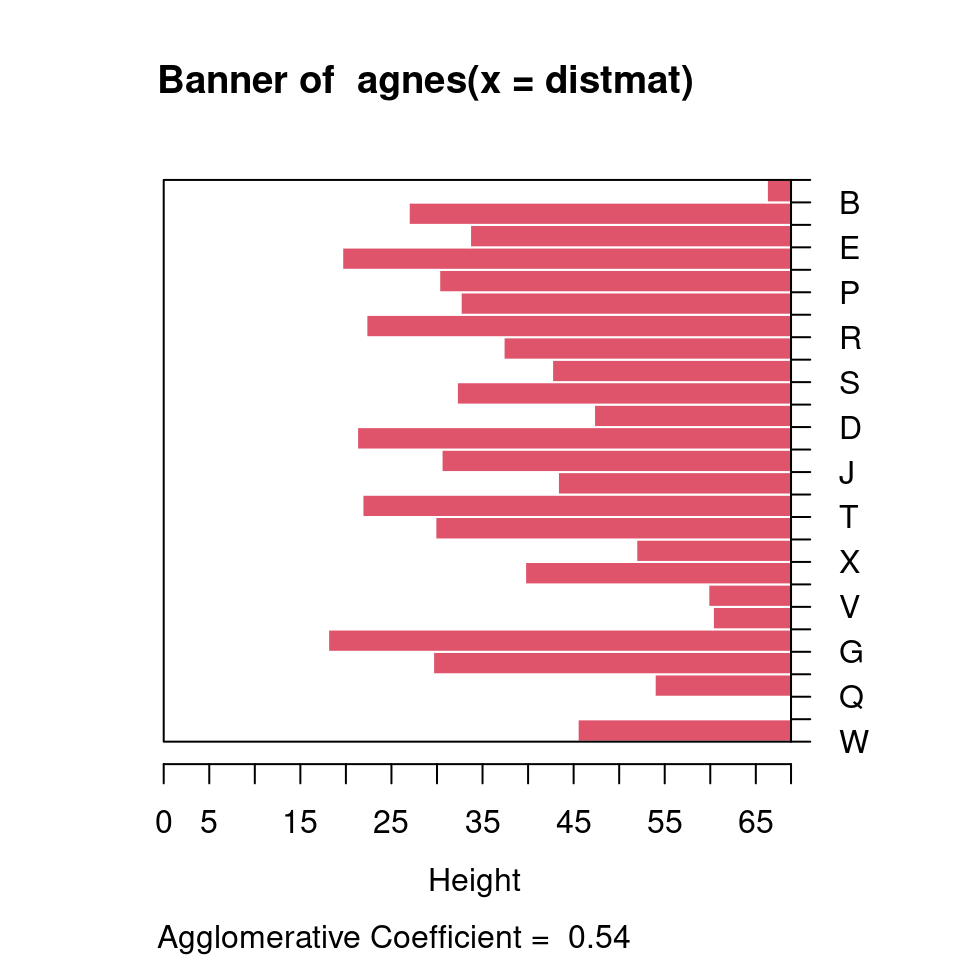
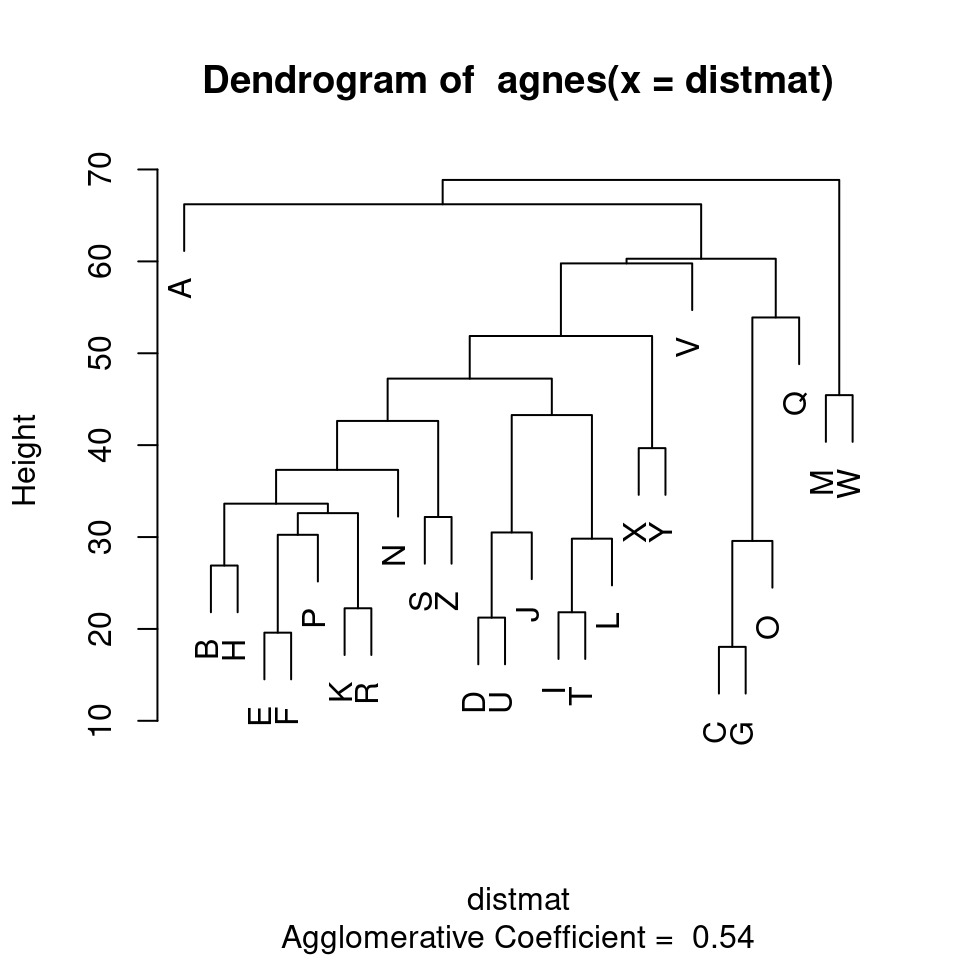
The standard display plot is sometimes not very polished. The ggdendro package provides a ggplot-based visualization:
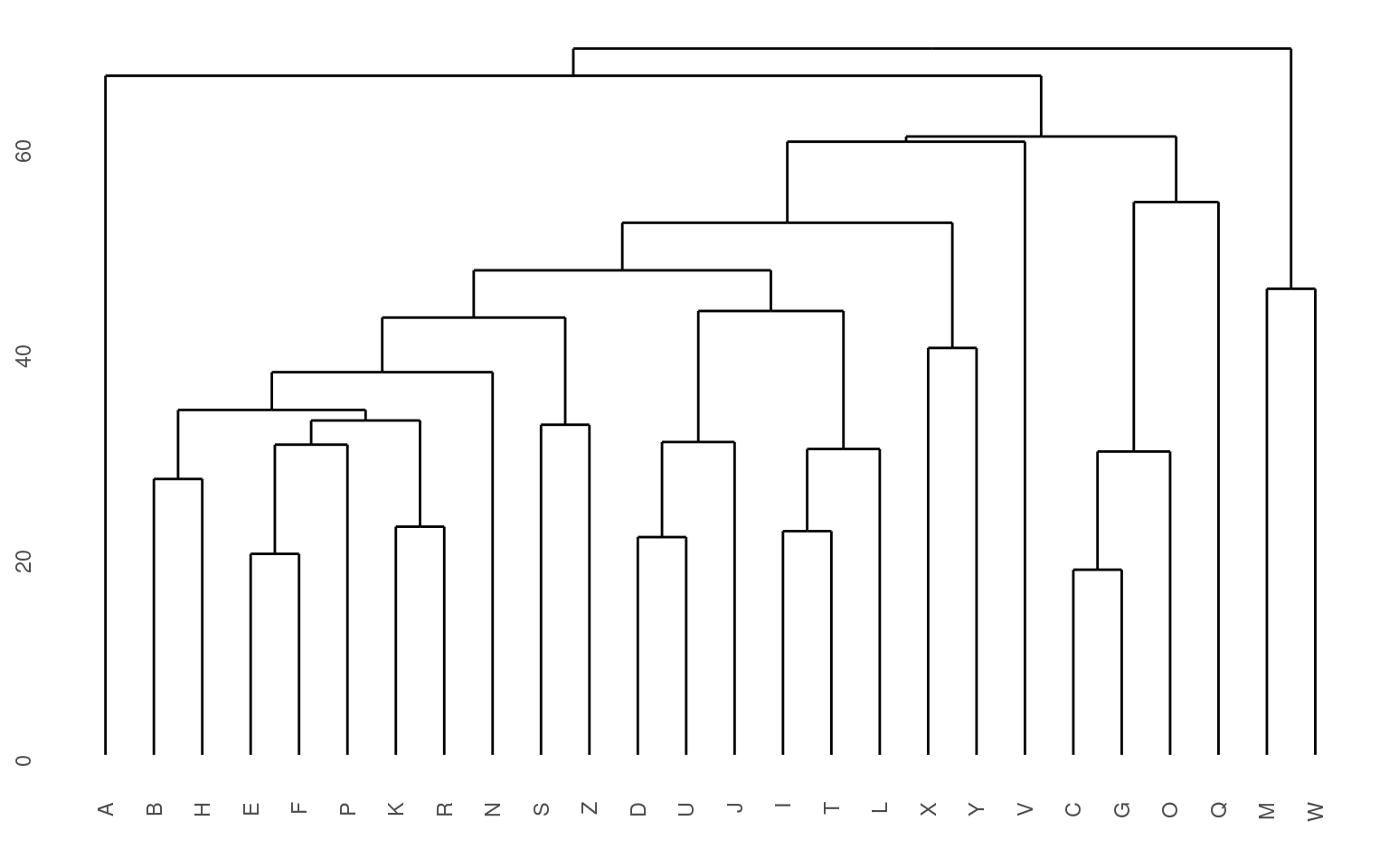
Notice that at the very bottom, we typically have visually-similar letters grouped. As you move higher, there are larger clusters that are more broadly similar. But dissimilarity is less clear. With appropriate distance measures, a hierarchical clustering is an ‘’ultrametric’’. Here, we interpret the dissimilarity between two things is the height of the cluster containing them both. Here, A, is dissimilar to everything; C, G, O, and Q are in a cluster, with Q being somewhat least well fit, and so on. Ultrametric spaces are convenient when the similarity between two things only matters locally, and if you get far away everything is essentially equally dissimilar.
The cluster library provides a set of functions for creating hierarchical and other clusters. They allows you to either specify the raw data (i.e., a feature space) or a distance metric. If you specify the raw data, it will compute a distance metric based on either euclidean or manhattan distance. Regardless of how you do it, you have the same problems as we experienced with earlier distance-based techniques like KNN clustering and MDS–you may need to normalize and weight features to get a good solution.
Warning…if you give it a distance measure but don’t transform it into one using as.dist, it can still give you something that looks OK, but is wrong. Compare the following, using the ‘agnes’ function. Remember that distmat0 matrix, which was the original raw data; distmat is the one that had been turned into a distance object.
library(gridExtra)
library(ggplot2)
p1 <- ggdendrogram(dendro_data(agnes(distmat)))
p2 <- ggdendrogram(dendro_data(agnes(distmat0)))
grid.arrange(p1, p2)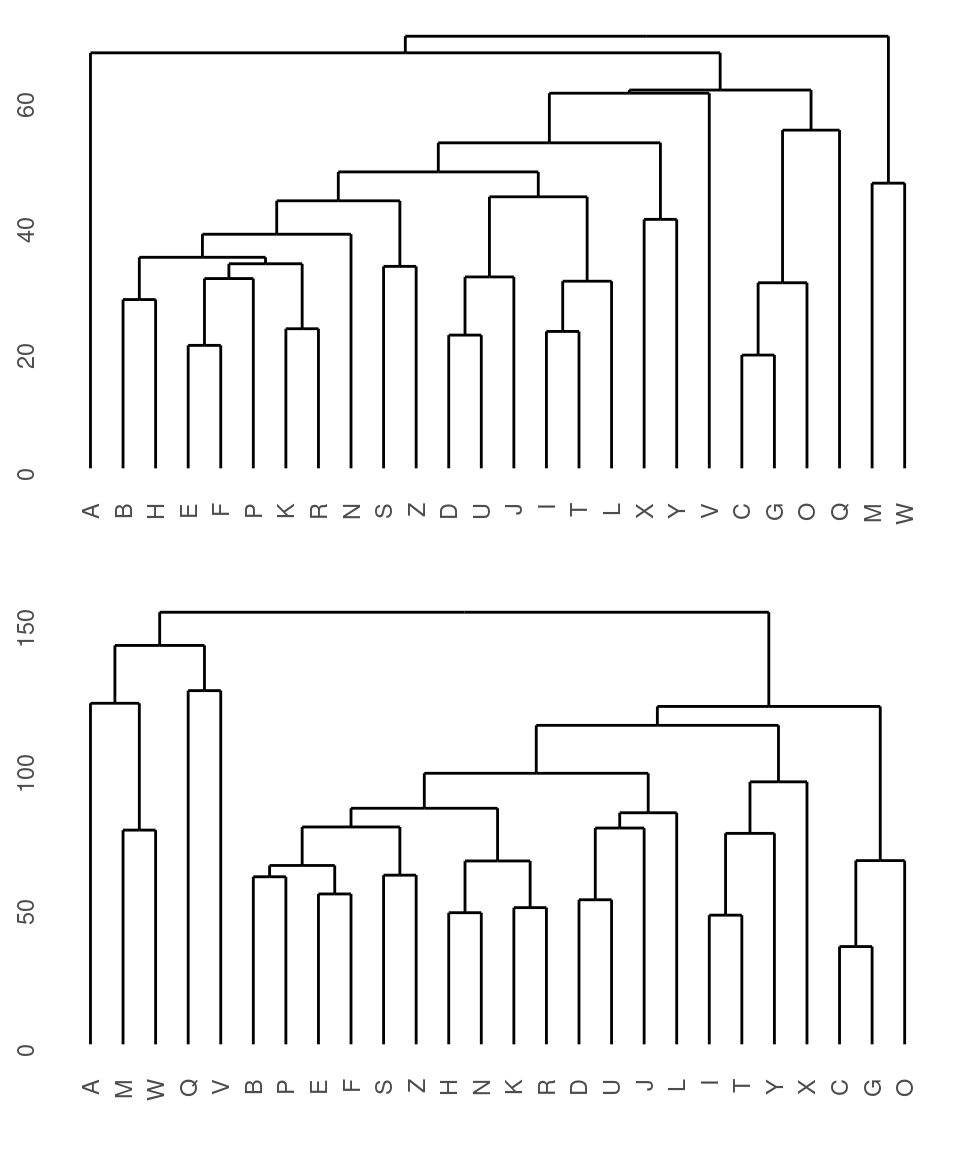 They both look sort of reasonable, but the first one is better. The
second one is treating the distance matrix as if it were a set of
features–it then creates a distance matrix based on these features,
which ends up being fairly similar but not identical. In some cases, it
could be very different, so you need to be careful about what goes into
these functions.
They both look sort of reasonable, but the first one is better. The
second one is treating the distance matrix as if it were a set of
features–it then creates a distance matrix based on these features,
which ends up being fairly similar but not identical. In some cases, it
could be very different, so you need to be careful about what goes into
these functions.
If you specify a set of features, you also can specify the type of metric used to compute a distance. The two available are euclidean and manhattan. Euclidean distance is just distance in space as the crow flies. Manhattan distance takes the deviation along each dimension and sums them–it is distance as you would need to travel along a city block scheme. The second is often better if you have independent features that don’t trade off.
Agglomerative approaches
The agglomerative approach implemented within the agnes
function starts by finding pairs that go together, and then build up
from the bottom. Let’s look more carefully at what happens:
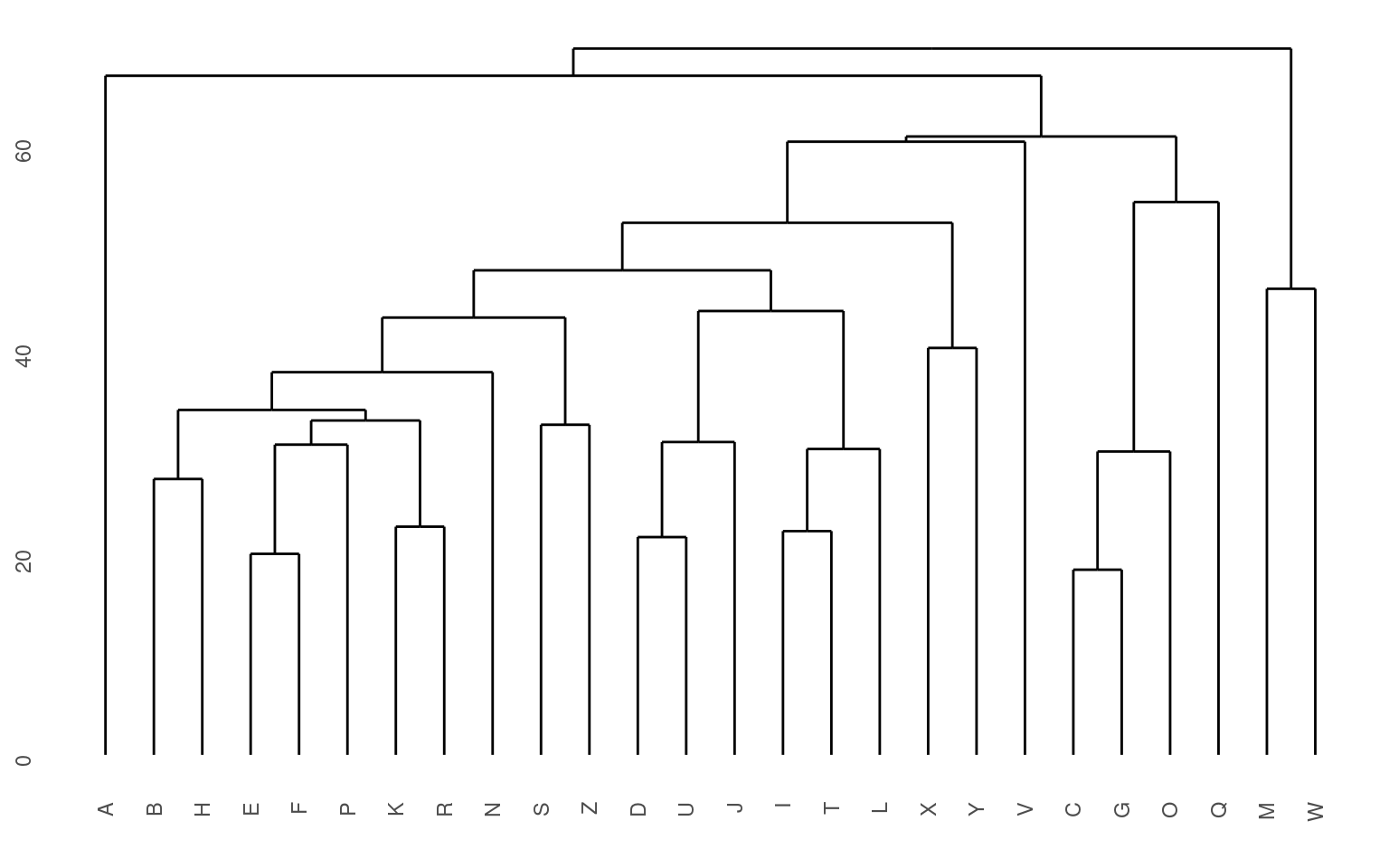
Although agnes can handle a distance matrix, you can also give it a set of feature-values, and it will compute that matrix directly. Remember that these features are developed with a different method than the subjective ratings data we have looked at so far.
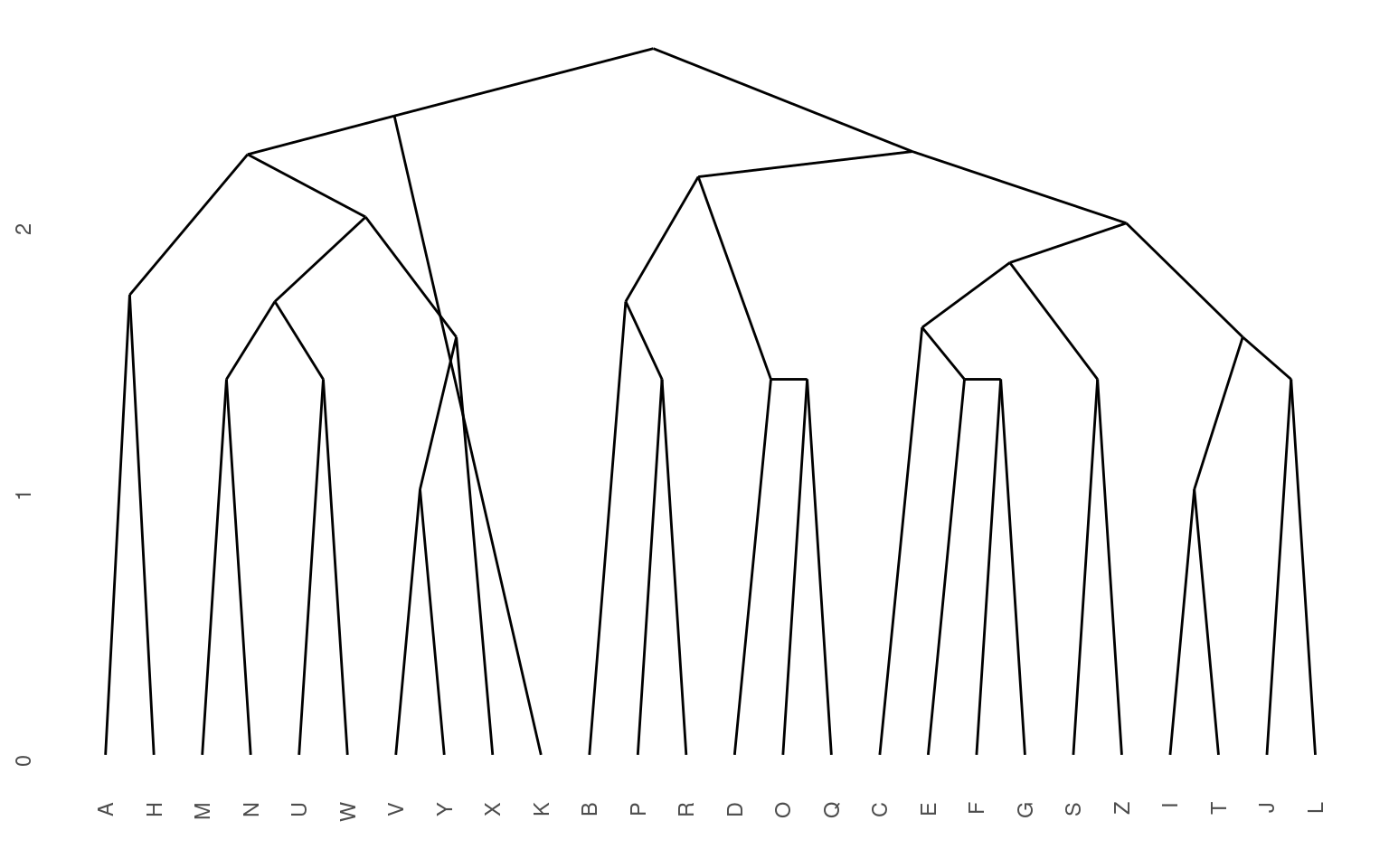
Here, we can see that both clustering solutions capture similar pairs fairly well. Both group E and F together, and put M and W close together. If we look at higher-level clusters, both group round letters together in one group. However, the higher-level structures seem a bit inconsistent. If we wanted to capture the large-scale structure first, we could use a divisive approach; trying to find the best splits from the large-scale data and iteratively dividing.
Divisive Approaches
A second method is to take the entire data set and first find the best way to divide it into two, and then divide those into two, and so on. This is more appropriate if you are more interested in a large-scale class structure. For example, if you had similarity ratings of hundreds of birds, you’d expect birds of the same species to be together at the bottom, but this maybe not as interesting as large-scale divisions (maybe between land and sea birds). In that case, you might consider a divisive approach, which is provided by the diana function.
d <- diana(distmat)
p1 <- ggdendrogram(dendro_data(d))
d2 <- diana(features)
p2 <- ggdendrogram(dendro_data(d2))
grid.arrange(p1, p2, ncol = 2)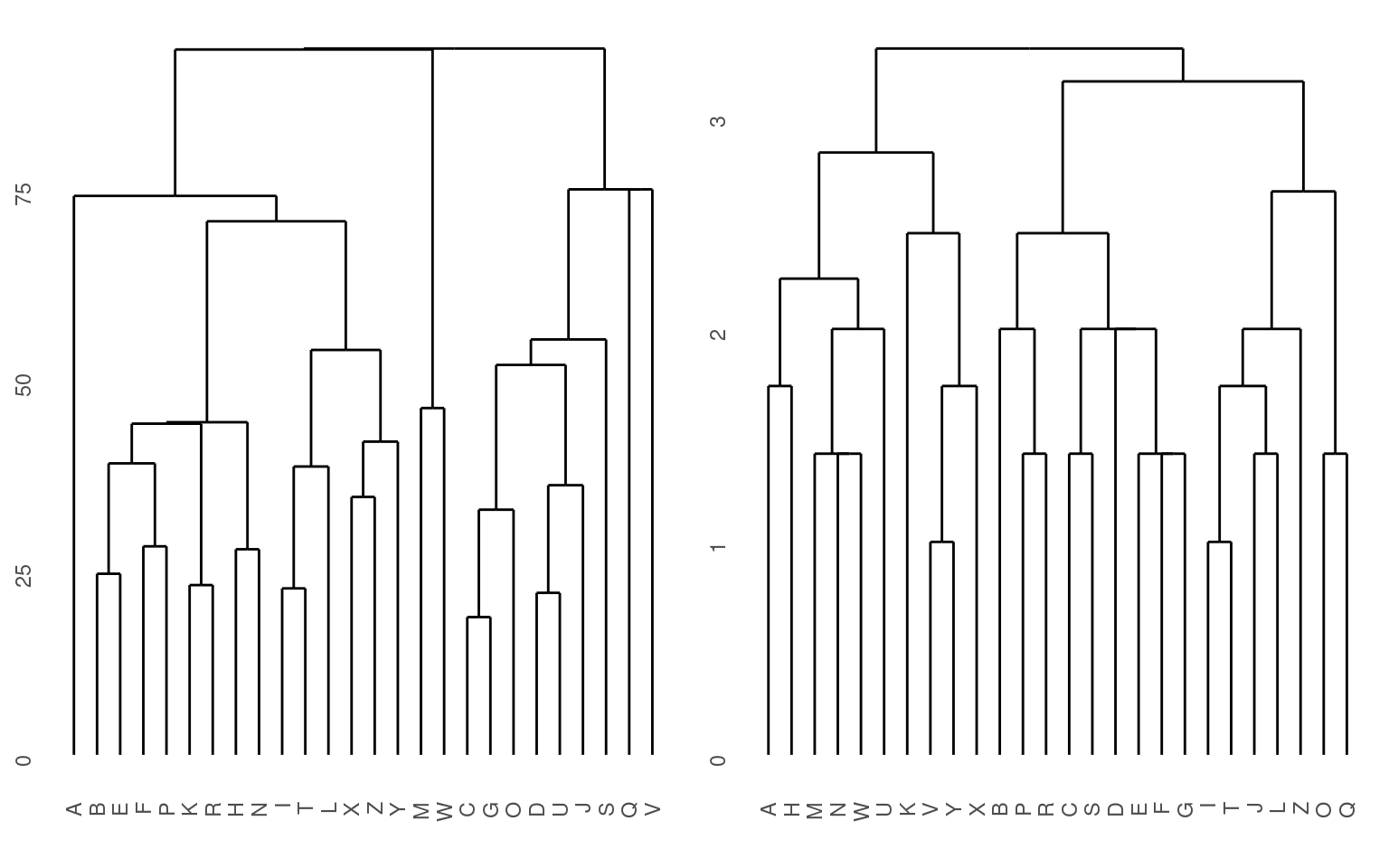
Notice that here, it perhaps does a better job of separating the curved letters from the boxy letters and the letters with diagonals.
Linkage methods of cluster similarity
For agglomerative clustering, the main way to control the outcome is to control how you compute the dissimilarity of a group, or of a group to a new item. These are influnced by the method argument, which can take on values: * single (essentially the distance from the new point to any element of the group) * average (average distance between point and all points in group) * complete (the largest distance from new point to anything in the group) * ward (undocumented) * weighted (some sort of weighted average) * flexible and gaverage (more detailed control)
If we compare some of these alternatives (so far we have used ‘average’, which is the default). In general, these are applicable to both agglomerative and divisive approaches
a2 <- agnes(distmat, method = "single")
a3 <- agnes(distmat, method = "complete")
a4 <- agnes(distmat, method = "ward")
a5 <- agnes(distmat, method = "weighted")
p2 <- ggdendrogram(dendro_data(a2)) + labs(title = "Single")
p3 <- ggdendrogram(dendro_data(a3)) + labs(title = "Complete")
p4 <- ggdendrogram(dendro_data(a4)) + labs(title = "Ward's Method")
p5 <- ggdendrogram(dendro_data(a5)) + labs(title = "Weighted")
grid.arrange(p2, p3, p4, p5, ncol = 2)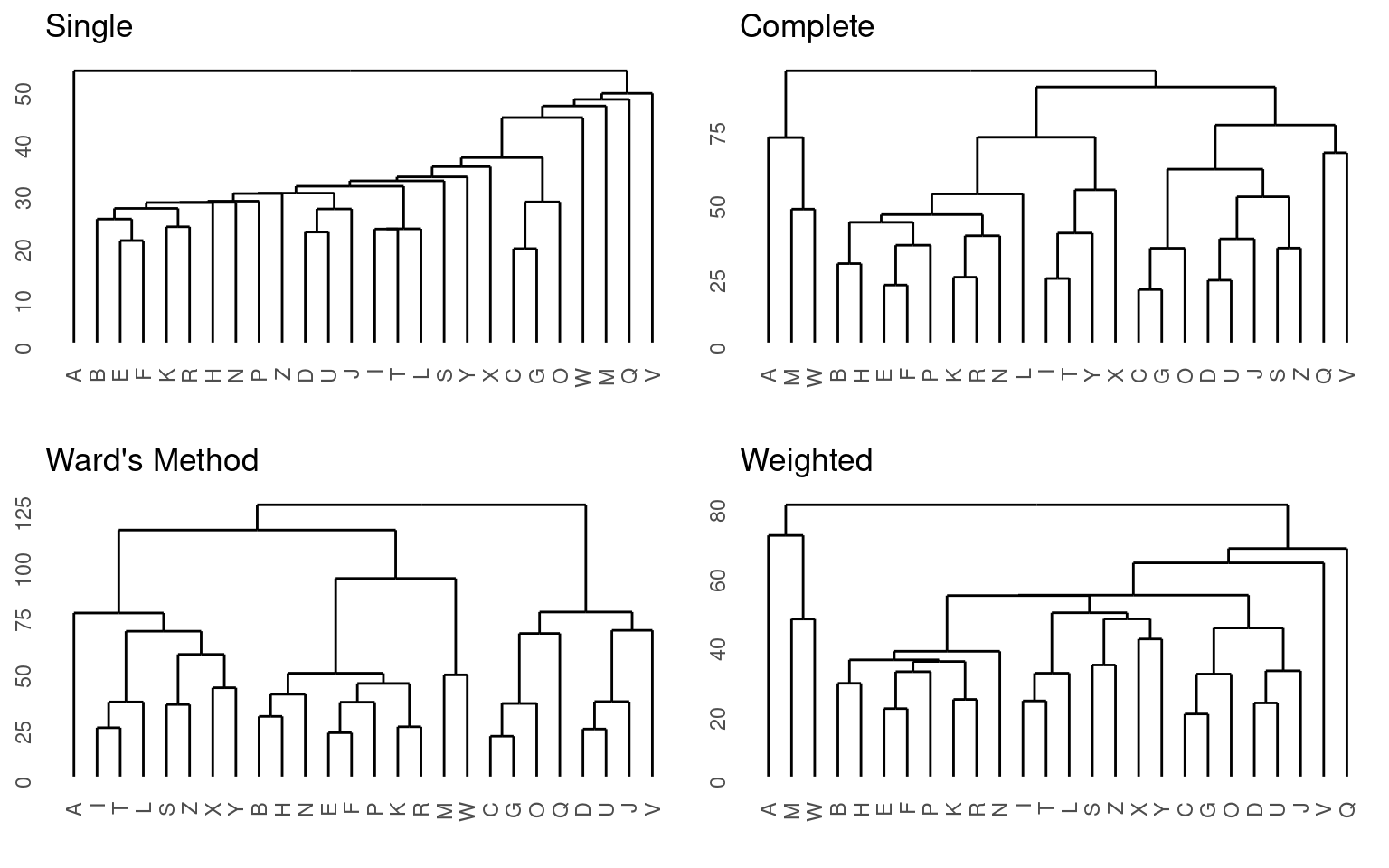
These different methods seem to have large differences in the outcome. The single-linkage model is pretty terrible. This is typical—it sort of links one next-closest item at a time into a chain. Single-linkage models are efficient to calculate because they pick the minimum pairing, but efficiency is not usually a huge concern, and so it is typically not a good idea to use single-linkage. Complete linkage takes the opposite approach, and all of the remaining solutions are pretty reasonable.
Exercise: for the feature-rating data, complete the different clustering methods and linkage methods, and compare the results
## Example:
a.rs <- agnes(features, method = "single")
d.rs <- diana(features)
p1 <- ggdendrogram(dendro_data(a.rs))
p2 <- ggdendrogram(dendro_data(d.rs))
grid.arrange(p1, p2, ncol = 2)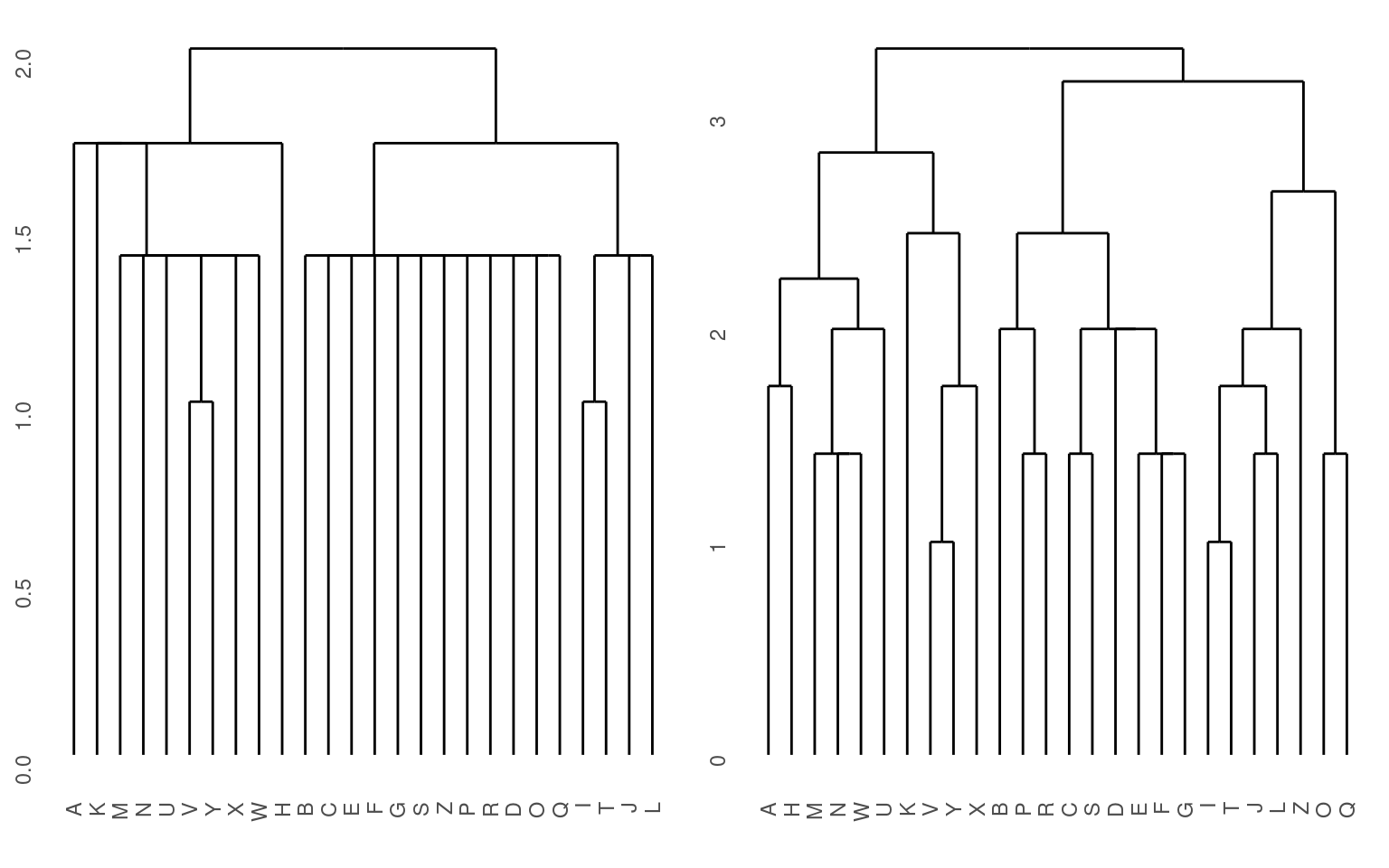 There are some additional clustering methods available within the
cluster library that are worth exploring. In comparison to the
agglomerative and divisive methods that are hierarchical (and build a
complete tree of nested clusters), other methods are ‘finite’ in that
they assume a fixed number of clusters. These include k-means
clustering, and several variations available within the cluster library.
In upcoming modules, we will also learn about finite mixture modeling,
which is a probability-based model of clustering.
There are some additional clustering methods available within the
cluster library that are worth exploring. In comparison to the
agglomerative and divisive methods that are hierarchical (and build a
complete tree of nested clusters), other methods are ‘finite’ in that
they assume a fixed number of clusters. These include k-means
clustering, and several variations available within the cluster library.
In upcoming modules, we will also learn about finite mixture modeling,
which is a probability-based model of clustering.
Finite Clustering Approaches
A second general approach to clustering is to assume a fixed number of clusters exist, and then find the best configuration that matches these clusters. The simplest approach for this is k-means clustering, where \(k\) is the fixed number of clusters. Of course, if we start with a specific value for \(k\), we can obtain a solution and get a measure of the goodness-of-fit. Then, we can compare this solution to solutions provided by other values of \(k\), and try to choose a \(k\) that seems most reasonable.
There are a number of related approaches to this, including finite mixture modeling which we will deal with in a future unit.
There are three things to consider when evaluating a finite clustering:
- The clusters should not overlap very much (segregation)
- There should be clear boundaries between clusters (separation; Between/Within SS)
- The more clusters there are, we require stronger evidence (simplicity)
These three principles are logical desiderata for a clustering solution. We can always split a group of objects into two cleanly by drawing a line through the middle; this does not mean that there are two distinct clusters. We should really only accept a larger set of clusters if there is strong evidence of modularity, which can be demonstrated via separation–gaps between the clusters. In addition, hopefully the distinct clusters will be meaningfully interpretable as well.
For the most part, finite clustering approaches do not provide metrics about these three, and you cannot always get a good sense of whether any of these improve when you make a different choice. But users often are satisfied with solutions that violate one or more of these assumptions. See powerpoint slides in the supplemental materials for more discussion on this.
K-means clustering
K-means clustering (Macqueen, 1967) uses distance to identify group
membership. You specify the number (\(k\)) of clusters, and it adaptively sorts
observations into clusters, and then adjusts the centers of the clusters
to fit the observations. This is easy to implement by hand, but the
kmeans function that is part of the R default stats package
provides a reasonable solution. One big difference between hierarchical
clustering and k-means clustering is that k-means requires the ‘raw’
data, not the distance metric, and gives us clusters as defined by the
mean values on each feature. If we had just similarity data, we could
use MDS to infer features, and then use that inferred space to produce a
k-means solution.
Let’s start with a small value for \(k\): say 3.
B C D E F G I J L O P Q R S T Z K V X Y A H M N U W
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 3 3 3 3 3 3 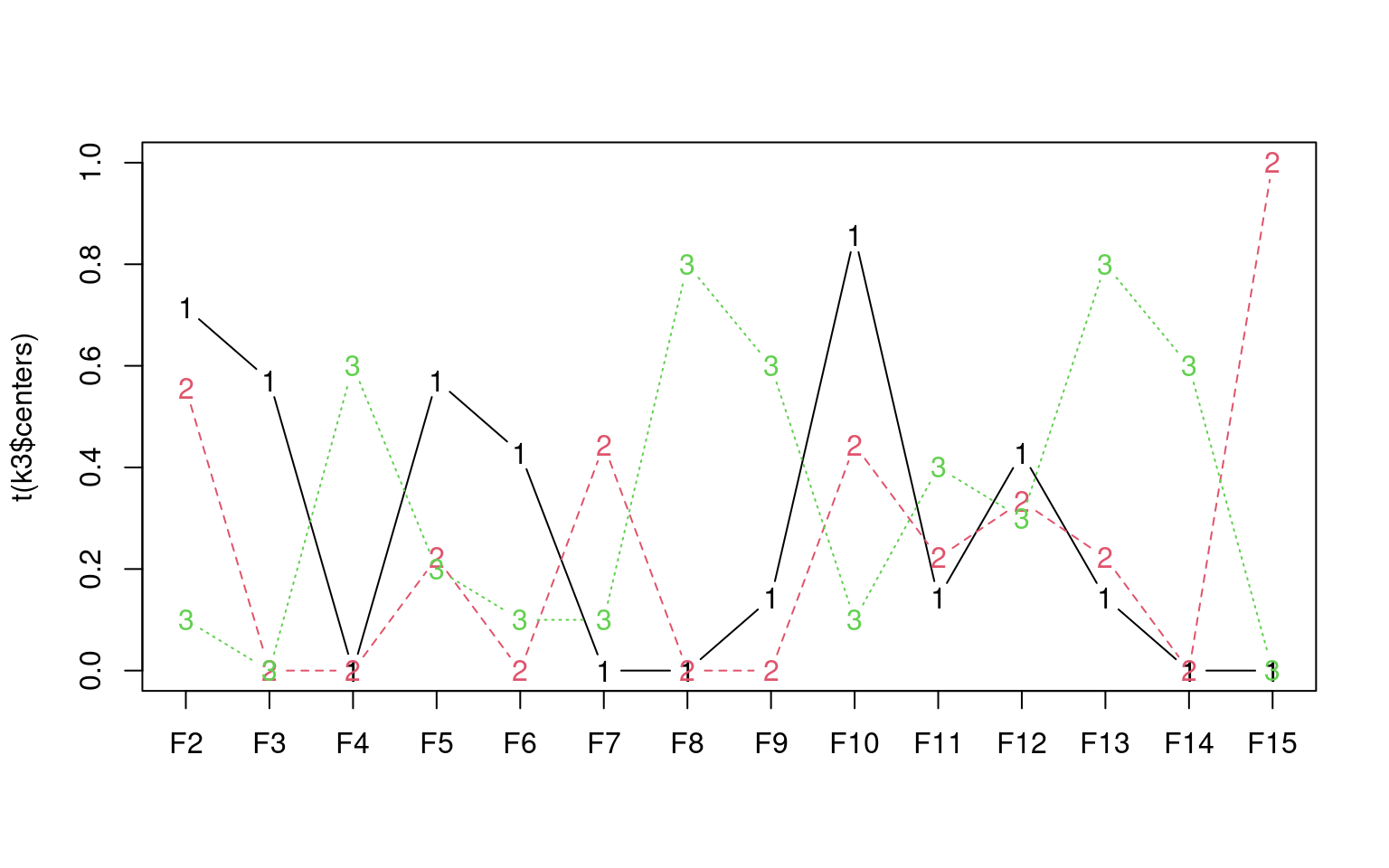
K-means clustering with 3 clusters of sizes 16, 4, 6
Cluster means:
V2 V3 V4 V5 V6 V7 V8 V9 V10 V11
1 0.625 0.25 0 0.3750000 0.1875000 0.25 0.0000000 0.0625000 0.6250000 0.1875
2 0.250 0.00 0 0.0000000 0.0000000 0.25 1.0000000 0.5000000 0.0000000 1.0000
3 0.000 0.00 1 0.3333333 0.1666667 0.00 0.6666667 0.6666667 0.1666667 0.0000
V12 V13 V14 V15
1 0.3750000 0.1875000 0.00 0.5625
2 0.5000000 0.7500000 0.75 0.0000
3 0.1666667 0.8333333 0.50 0.0000
Clustering vector:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
3 1 1 1 1 1 1 3 1 1 2 1 3 3 1 1 1 1 1 1 3 2 3 2 2 1
Within cluster sum of squares by cluster:
[1] 33.187500 5.000000 8.833333
(between_SS / total_SS = 34.8 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" If you run this multiple times without using the seed, you are likely
to get different solutions.
Here, each cluster is defined by the means on 14 dimensions. In this
solution, group 1 is highest on dimensions 2, 10, and 15; group 2 is
highest on 8 and 11, and group 3 is highest on 4. The letters are mapped
to the clusters as follows:
B C D E F G I J L O P Q R S T Z K V X Y A H M N U W
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 3 3 3 3 3 3 To help us visualize this, we can do an MDS:
initial value 21.040029
iter 5 value 18.744396
final value 18.712826
convergedplot(mds$points, pch = 16, cex = 3.5, col = k3$cluster)
text(mds$points[, 1], mds$points[, 2], LETTERS, col = "white")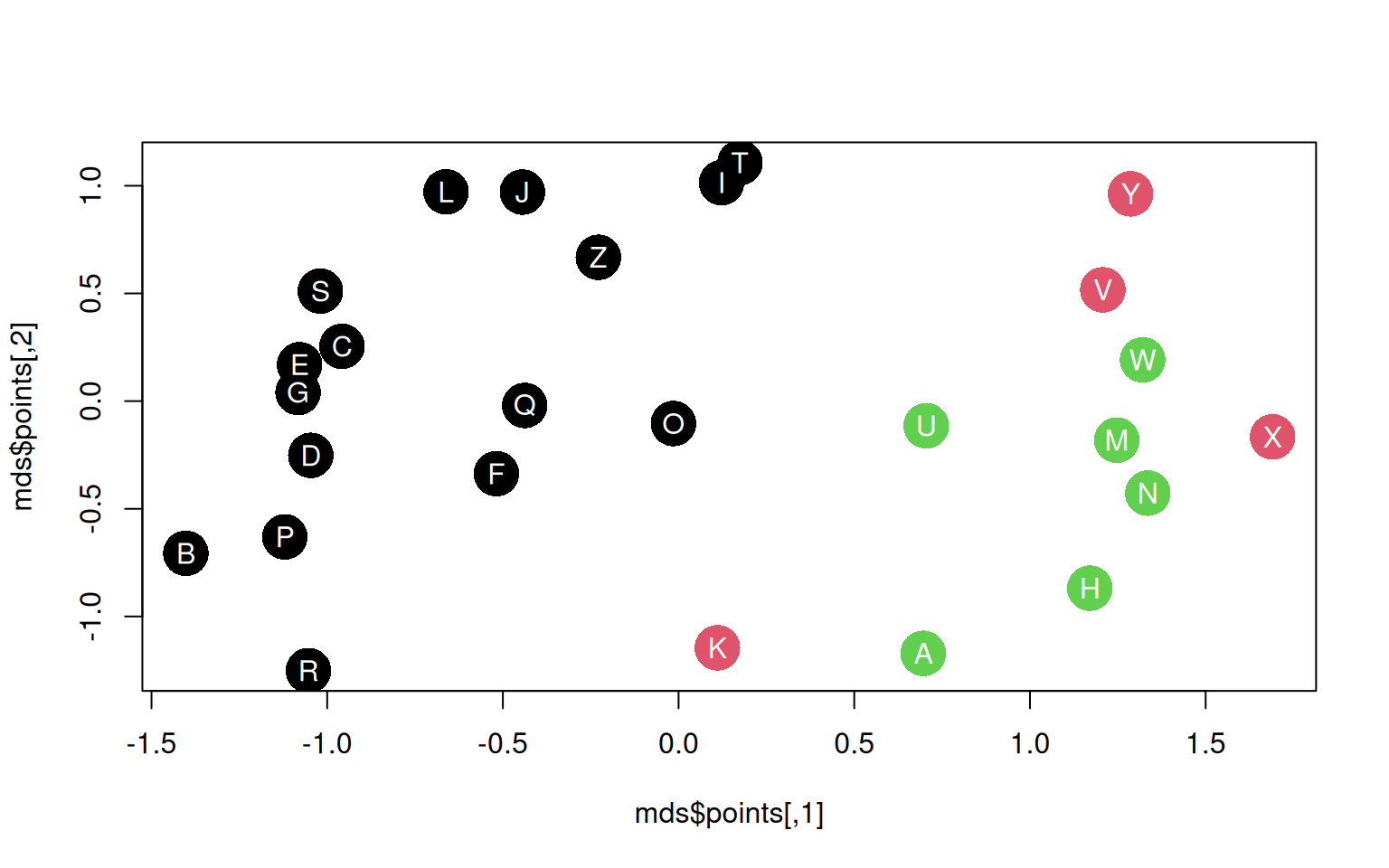
The MDS layout is not determined by the clusters at all, but it is determined by the same features that determine the clusters.
K-means provides a goodness of fit statistic, indicating the sum of squares by cluster. By dividing between-group sum-of-squares by within-group, you can figure out the proportion of variance accounted for within versus between clusters.
What happens to this when we look at different k-values?
Exercise: do a k-means clustering on the feature-based letter data, exploring the solutions and the sum-of-squares statistics.
Here is a starting point:
k2 <- kmeans(features, centers = 2)
k3 <- kmeans(features, centers = 3)
k4 <- kmeans(features, centers = 4)
k5 <- kmeans(features, centers = 5)
k10 <- kmeans(features, centers = 10)
k2$betweenss/k2$totss[1] 0.2515991[1] 0.3729668[1] 0.4665859[1] 0.5461417[1] 0.7357498plot(mds$points, pch = 16, cex = 3.5, col = k2$cluster)
text(mds$points[, 1], mds$points[, 2], LETTERS, col = "white")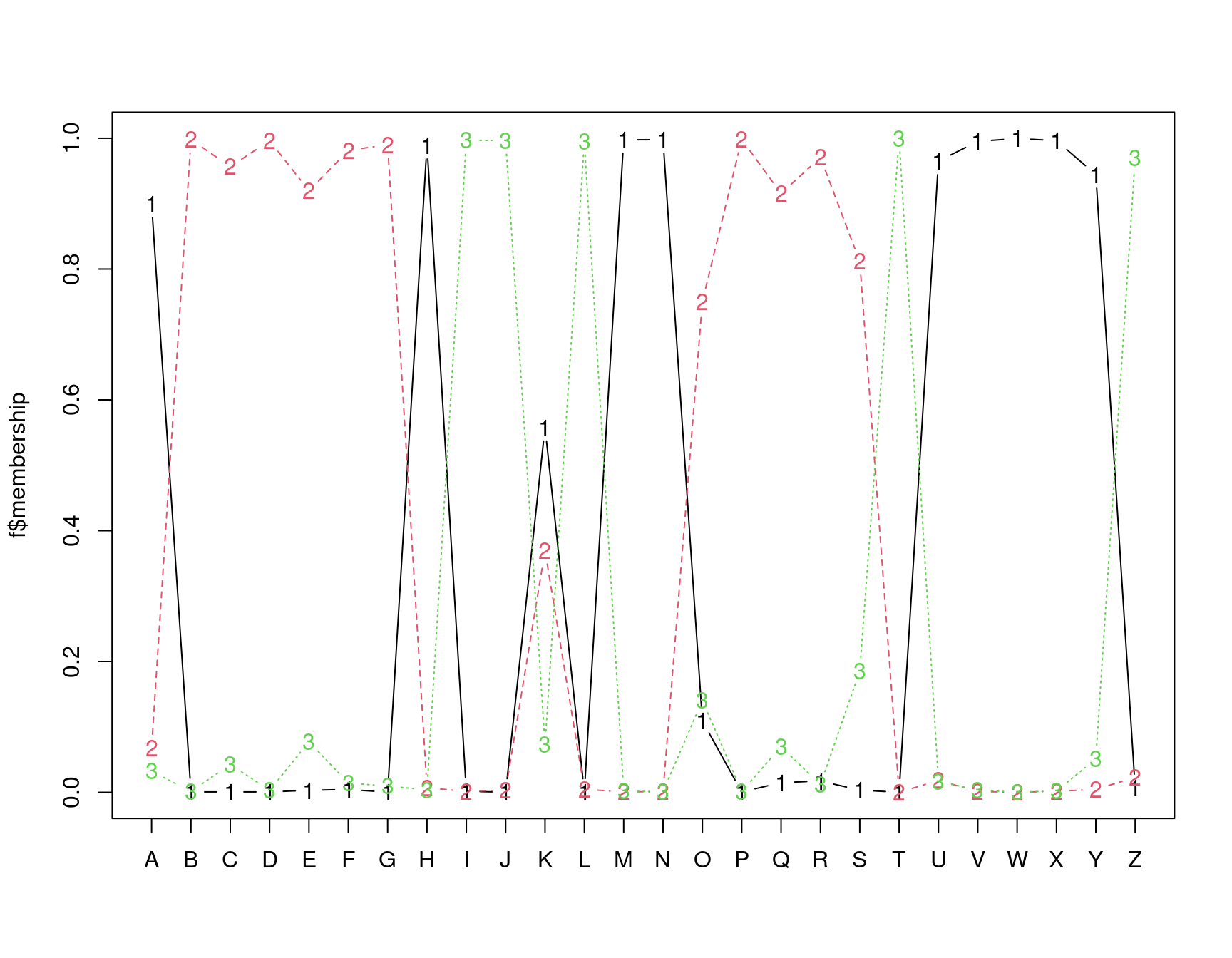
plot(mds$points, pch = 16, cex = 3.5, col = k5$cluster)
text(mds$points[, 1], mds$points[, 2], LETTERS, col = "white")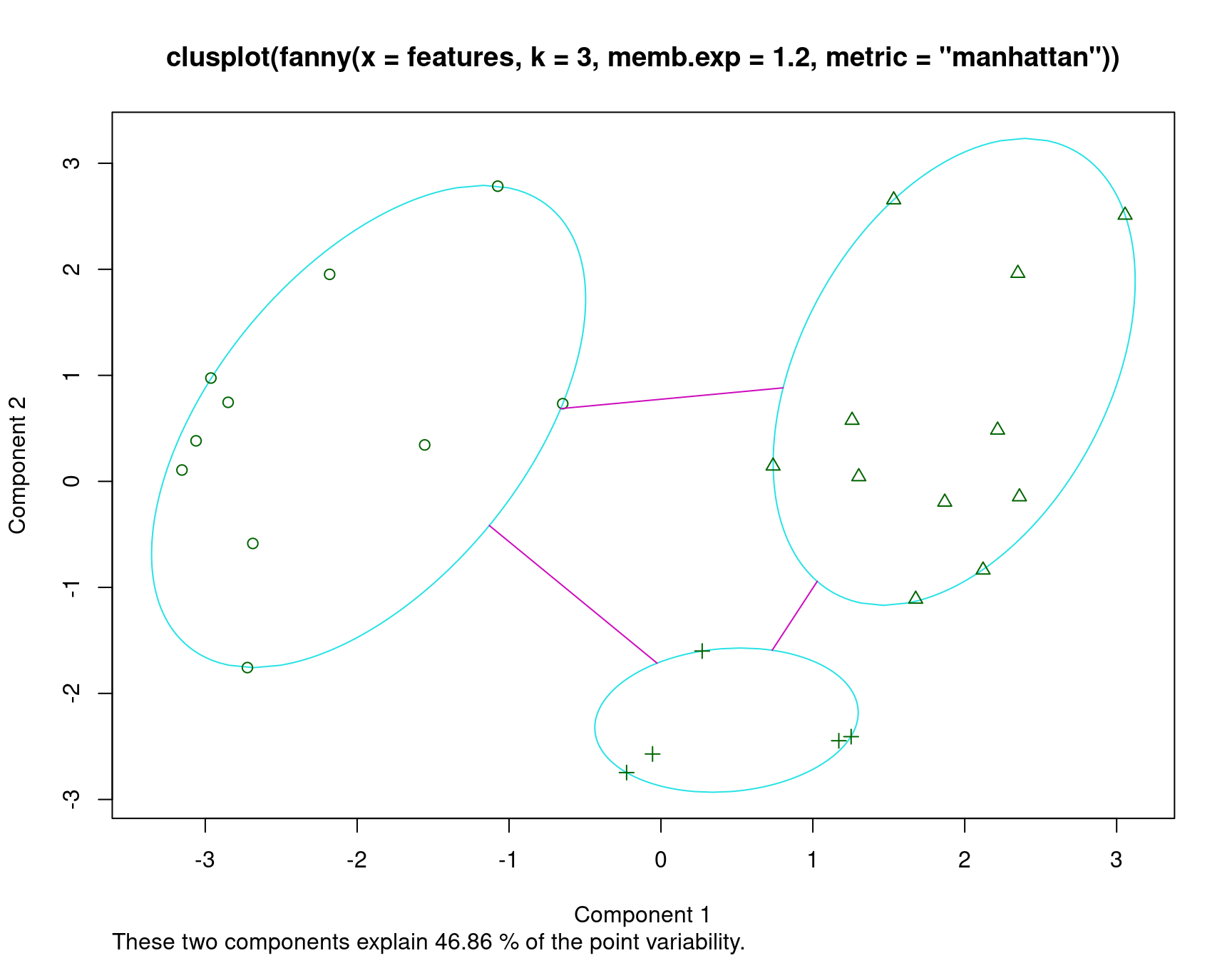
plot(mds$points, pch = 16, cex = 3.5, col = k10$cluster)
text(mds$points[, 1], mds$points[, 2], LETTERS, col = "white")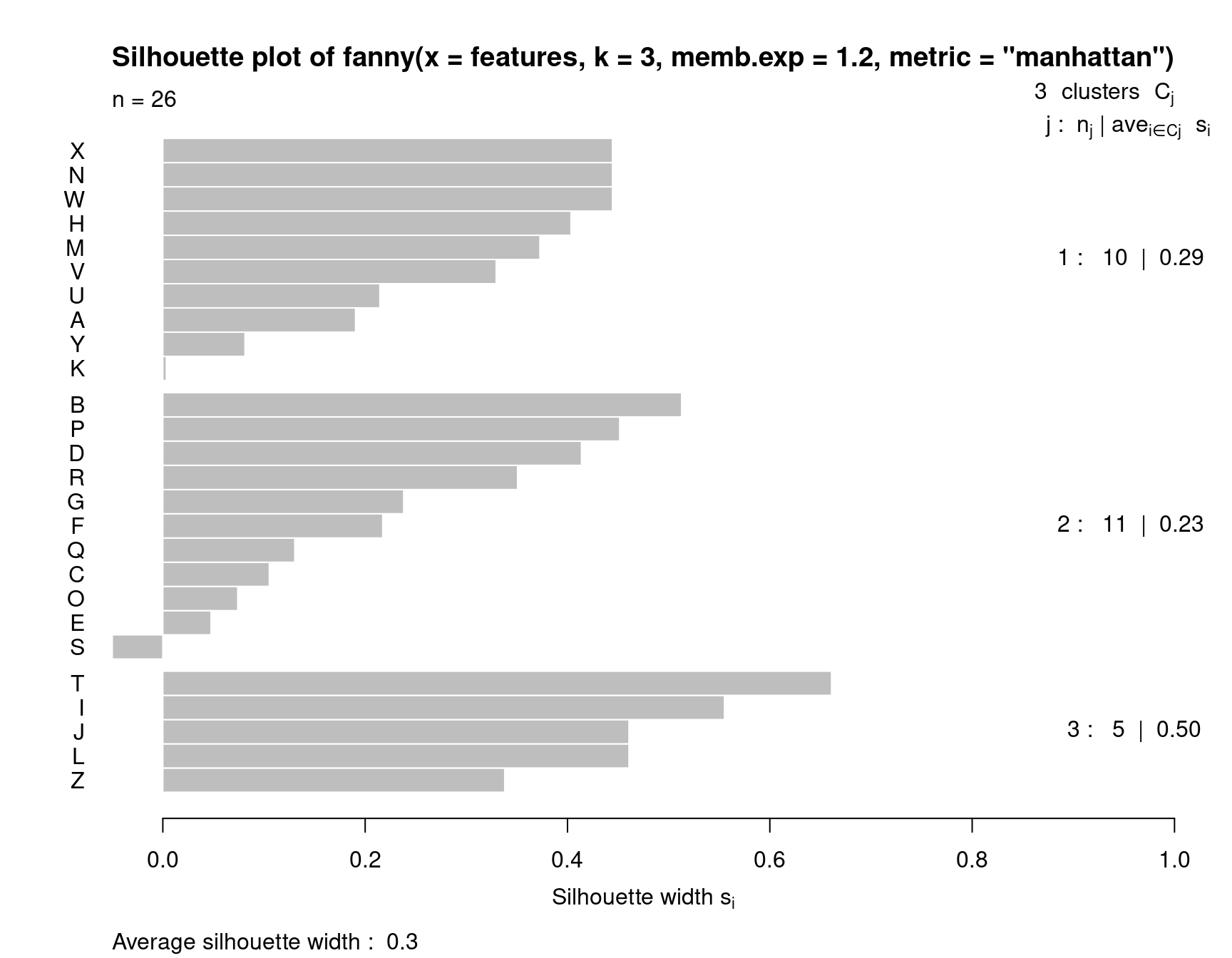 Here, the between/within rises from 26% to 73% as the number of groups
goes up to 10. That is, 73% of the total variance is being explained by
differences between groups. We’d prefer a smaller proportion, because
that means a strong similarity within group and dissimilarity across
groups. Here, we also notice a diminishing return for adding more
clusters after 4 or 5. For classic k-means clustering, these can only
provide rough guidelines for choosing k, but they are helpful
nevertheless.
Here, the between/within rises from 26% to 73% as the number of groups
goes up to 10. That is, 73% of the total variance is being explained by
differences between groups. We’d prefer a smaller proportion, because
that means a strong similarity within group and dissimilarity across
groups. Here, we also notice a diminishing return for adding more
clusters after 4 or 5. For classic k-means clustering, these can only
provide rough guidelines for choosing k, but they are helpful
nevertheless.
Maybe we want to look at the k5 solution:
C E F G P R S I J L T Z A H M N U W B D O Q K V X Y
1 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 4 4 4 4 5 5 5 5 This seems a bit better than the 3-cluster solution, as it tends to group together smaller sets of roughly-similar letters. But there are some that don’t really seem to fit well, and other clusters that seem similar to one another. Maybe we should consider a different approach that does not require the segregration property and allows partial membership in clusters.
Fuzzy clustering (FANNY)
Fanny clustering (in the cluster library) is sort of a fuzzy k-means, because each observation may have likelihood of belonging to several clusters. This is not exactly partitioning, but can be helpful in determining how well different observations fit into different clusters.
We will use the feature data for this, examining just three clusters.
Let’s use manhattan metric, because these are binary features. Also,
initial solutions were poor, and fanny recommended changing
the default memb.exp value, which appears to be a sort of soft-max
coefficient value.
Fuzzy Clustering object of class 'fanny' :
m.ship.expon. 1.2
objective 44.07947
tolerance 1e-15
iterations 24
converged 1
maxit 500
n 26
Membership coefficients (in %, rounded):
[,1] [,2] [,3]
A 90 7 3
B 0 100 0
C 0 96 4
D 0 100 0
E 0 92 8
F 0 98 1
G 0 99 1
H 99 1 0
I 0 0 100
J 0 0 100
K 56 37 7
L 0 0 100
M 100 0 0
N 100 0 0
O 11 75 14
P 0 100 0
Q 1 92 7
R 2 97 1
S 0 81 19
T 0 0 100
U 97 2 2
V 100 0 0
W 100 0 0
X 100 0 0
Y 94 0 5
[ reached getOption("max.print") -- omitted 1 row ]
Fuzzyness coefficients:
dunn_coeff normalized
0.912930 0.869395
Closest hard clustering:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 2 2 2 2 2 2 1 3 3 1 3 1 1 2 2 2 2 2 3 1 1 1 1 1 3
Available components:
[1] "membership" "coeff" "memb.exp" "clustering" "k.crisp"
[6] "objective" "convergence" "diss" "call" "silinfo"
[11] "data" 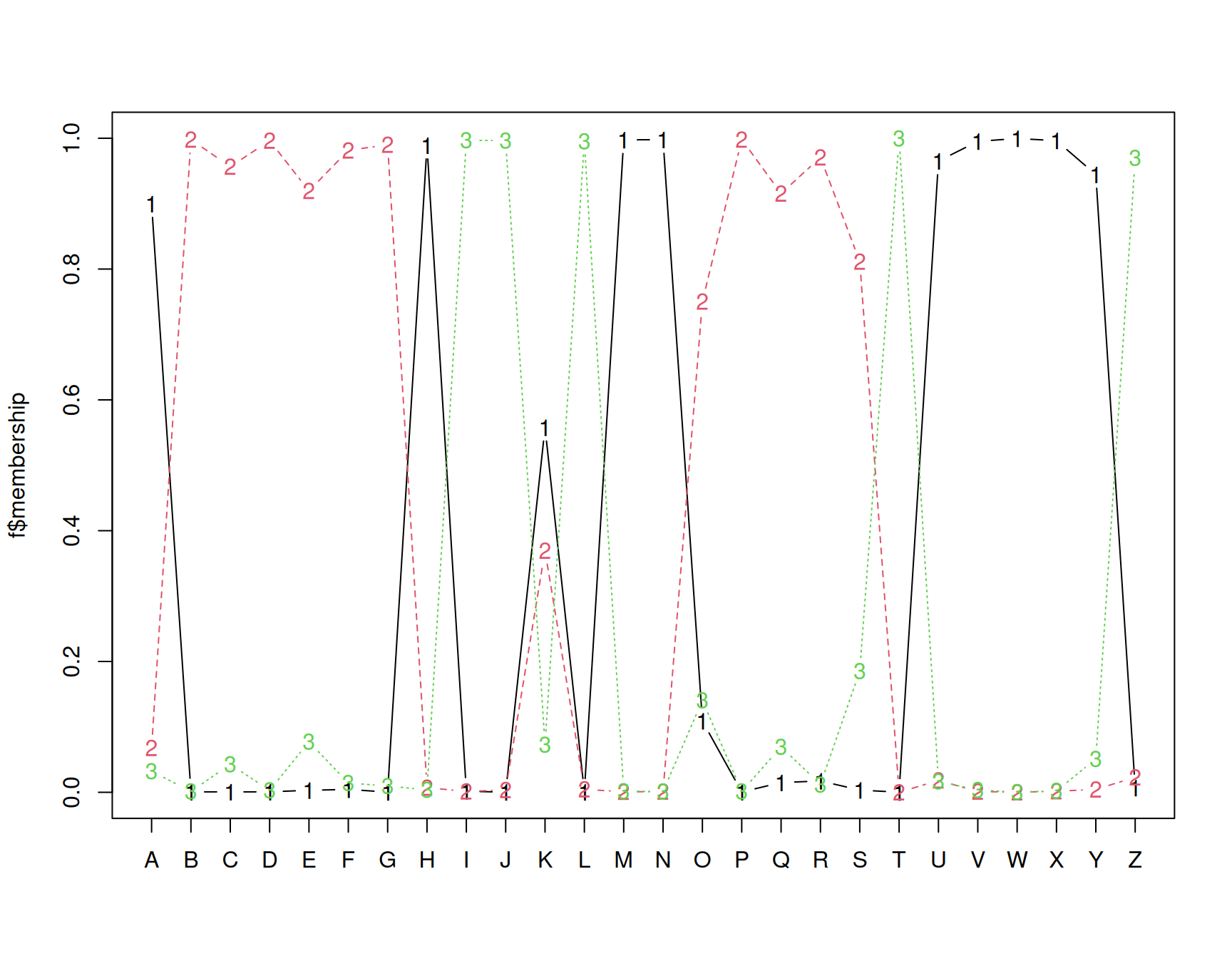
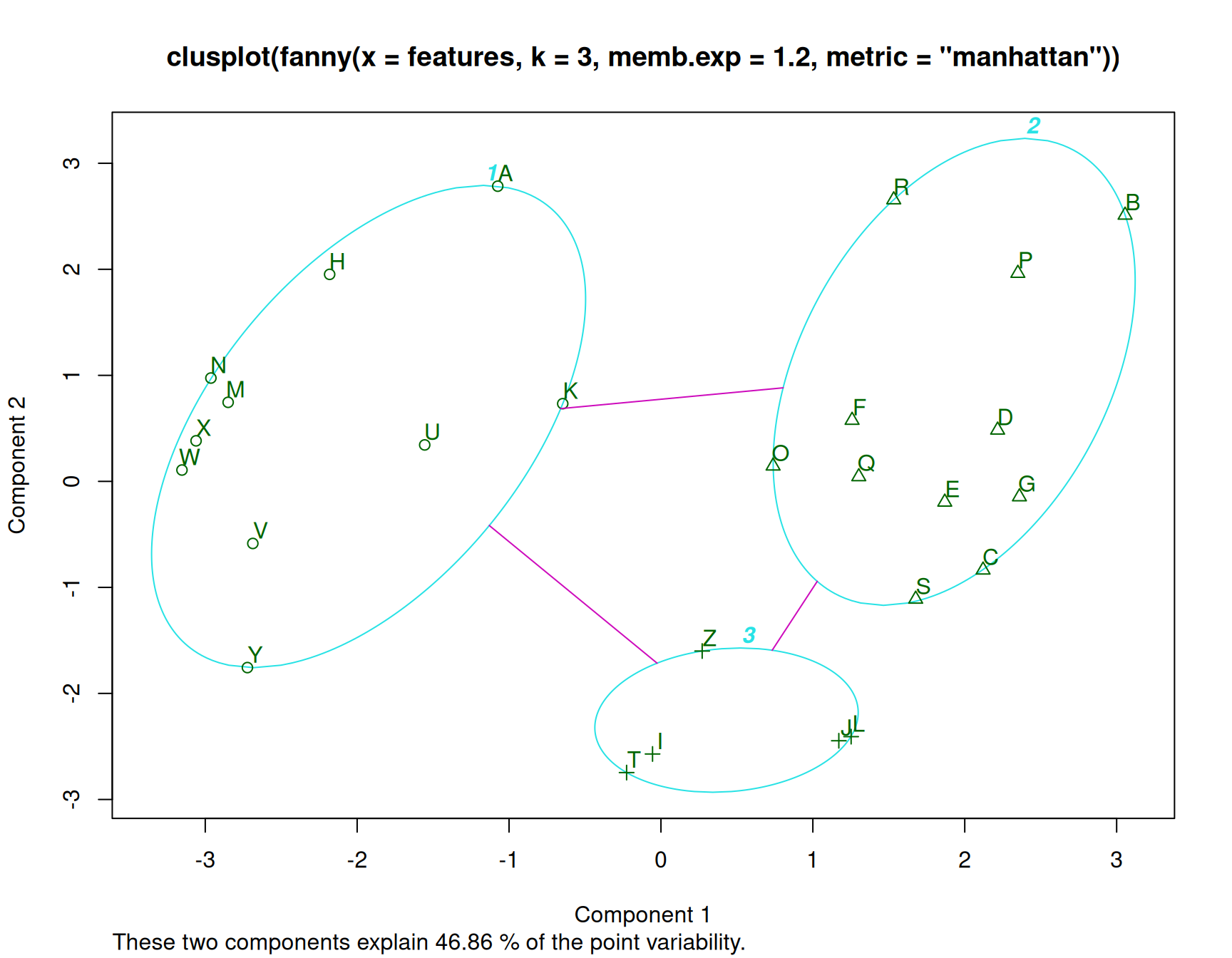
In this analysis, we have assumed three clusters. The matplot we performed returns a membership value, which indicates a fuzzy membership level in each of the clusters. Some values are unambiguous (M and N), but others are less so, (like K). If we then place the item in the best group, we can get a measure of how well it fits that group using a silhouette plot. The horizontal width of the silhouette plot shows how well each item is described by the cluster it ended up in. Sometimes, a few elements will fall ‘below the waterline’, meaning that they are not well described by the cluster they are placed in. For example, K and S are poor. According to the fuzzy membership number, although K is most likely to be in group 1, it is about equally likely to be in either group 3 or 2.
Fanny also returns some fuzzyness coefficients that indicate how well the model works (the dunn coefficient). This might be used to compare to other choices of k.
Exercise: Do a fanny clustering for different k-sizes and compare results.
Partition around Mediods (PAM)
The PAM clustering approach (also in the cluster
library) assumes a fixed number of ‘mediods’ that you specify. These
mediods are like centroids, but are exemplars that are in the data,
rather than a ‘prototype’ or average mixture of all of the elements in
that group. Like agnes and diana,
pam can use either a distance matrix or raw data (in which
case you need to specify the metric.) It also provides a silhouette
plot. Let’s look at the original letter data, with k=2,3, and 4:
p2 <- pam(distmat, k = 2)
p3 <- pam(distmat, k = 3)
p4 <- pam(distmat, k = 4)
par(mfrow = c(1, 3))
plot(p2)
plot(p3)
plot(p4)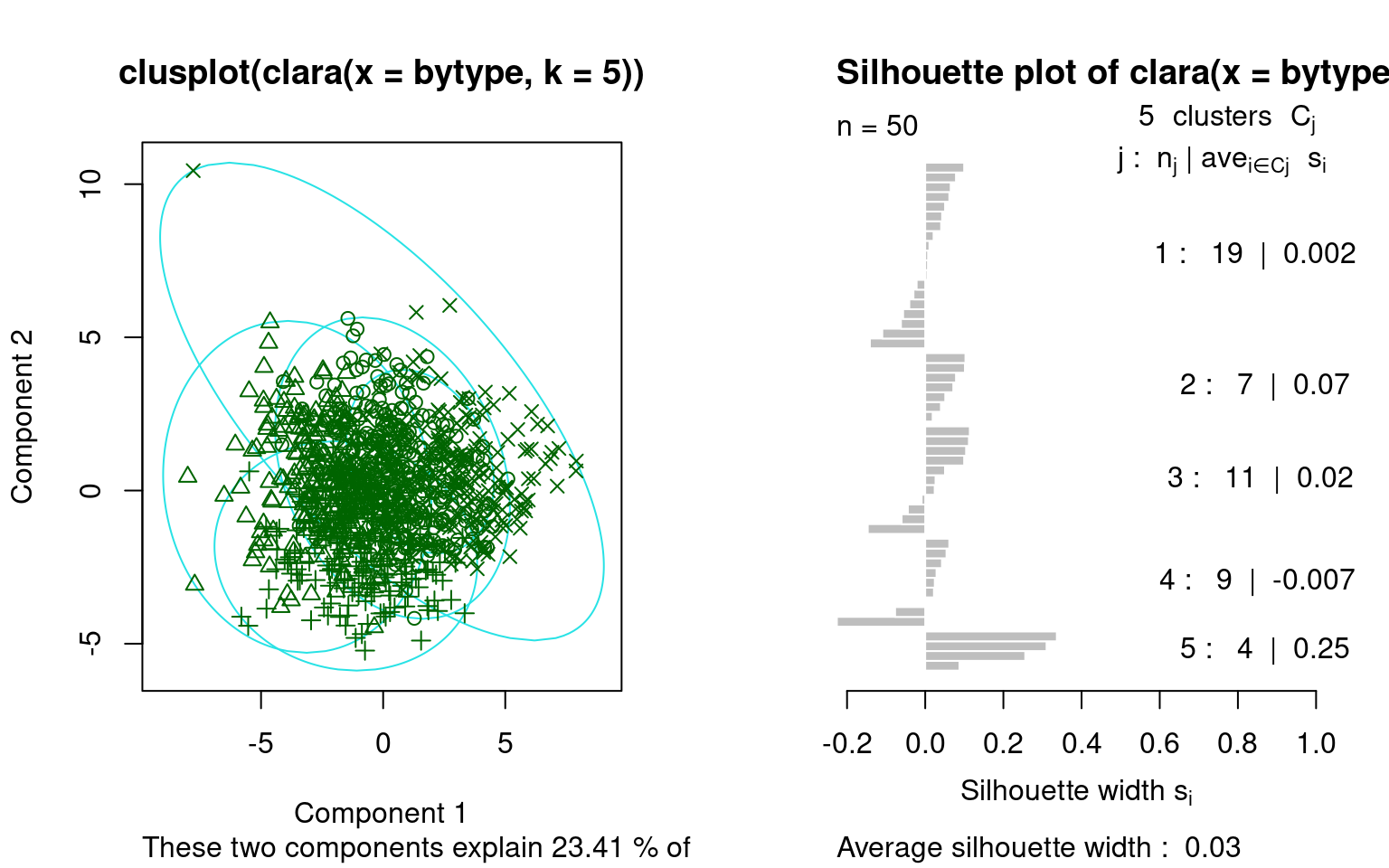
Medoids:
ID
[1,] "5" "E"
[2,] "3" "C"
[3,] "9" "I"
[4,] "23" "W"
Clustering vector:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
1 1 2 1 1 1 2 1 3 3 1 3 4 1 2 1 2 1 1 3 1 3 4 1 3 1
Objective function:
build swap
28.65732 28.65732
Available components:
[1] "medoids" "id.med" "clustering" "objective" "isolation"
[6] "clusinfo" "silinfo" "diss" "call" plot(p2, which = 1, labels = 2) #clusterplot
plot(p3, which = 1, labels = 2) #clusterplot
plot(p4, which = 1, labels = 2) #clusterplot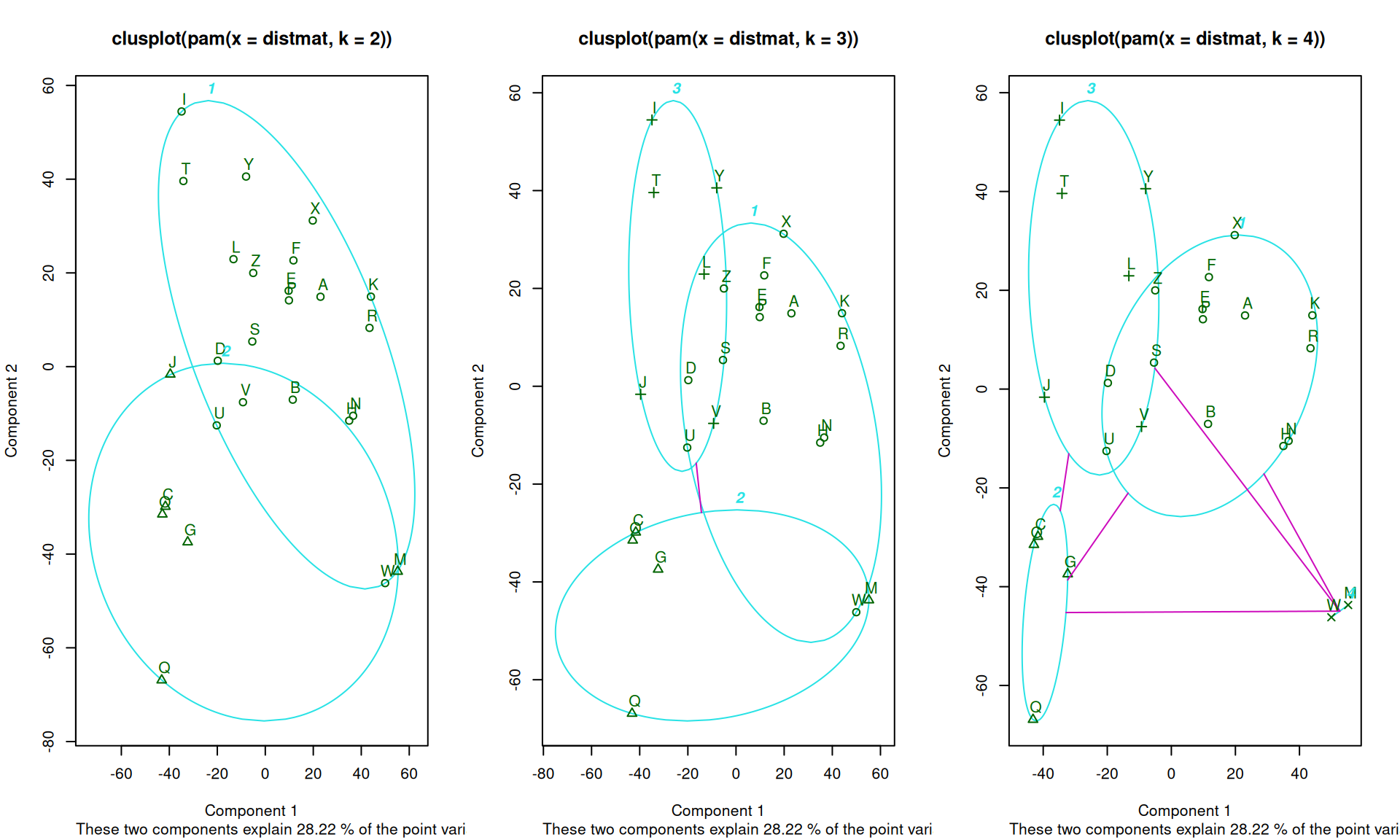
These again show a goodness of fit between each point in a cluster and all other points in that cluster. Note that they rank order the observations in each based on the silhouette width, which is sort of a typicality of the observation. Usually, the mediod has the highest silhouette value, but not always. For example, for k=4, the mediods were E, C, I, and W. The silhouette plot is not showing the exact values used to make the clustering, (distance to mediod), but rather an overall average similarity. Negative values indicate poor fit, and may mean more clusters are needed.
PAM is interesting because it uses just the similarity values between cases. It does not need to recompute any similarities to the center, because each center is one of the cases. It also gives a center item that can be used to label the group–rather than considering an arbitrary point in an arbitrary space. But it requires the similarity or distance metric, whose size is \(n*(n-1)/2\). This can get large as the data set gets large, and so may get inefficient.
clara: PAM with a lot of data
If you have a lot of data, the similarity matrix is the square of the
number of elements, and it can get very large, and these methods can
grow very inefficient. the clara function handles larger
data sets. Instead of using a complete dissimilarity matrix, it instead
takes a set of features, and has efficient ways of calculating group
membership. We can use the big five data set to illustrate this. If we
want to identify clusters in this data set with 1,000+ people, that
would be more than 1,000,000 pairings of distances we would need to
calculate. Let’s consider the big-five data set, which had 1017
participants:
data <- read.csv("bigfive.csv")
dat.vals <- data[, -1] ##remove subject code
dat.vals[is.na(dat.vals)] <- 3
qtype <- c("E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "E", "A", "C", "N",
"O", "E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "E", "A", "C", "N", "O",
"E", "A", "C", "N", "O", "E", "A", "C", "N", "O", "O", "A", "C", "O")
valence <- c(1, -1, 1, 1, 1, -1, 1, -1, -1, 1, 1, -1, 1, 1, 1, 1, 1, -1, 1, 1, -1,
1, -1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, -1, -1, 1, -1, 1, 1, 1, -1, 1, -1, 1)
add <- c(6, 0, 0)[valence + 2]
tmp <- dat.vals
reversed <- t(t(tmp) * valence + add)
## reverse code questions:
bytype <- reversed[, order(qtype)]
key <- sort(qtype)
colnames(bytype) <- paste(key, 1:44, sep = "")Let’s do a clara clustering by people–which might be needed because we have so many people observed.
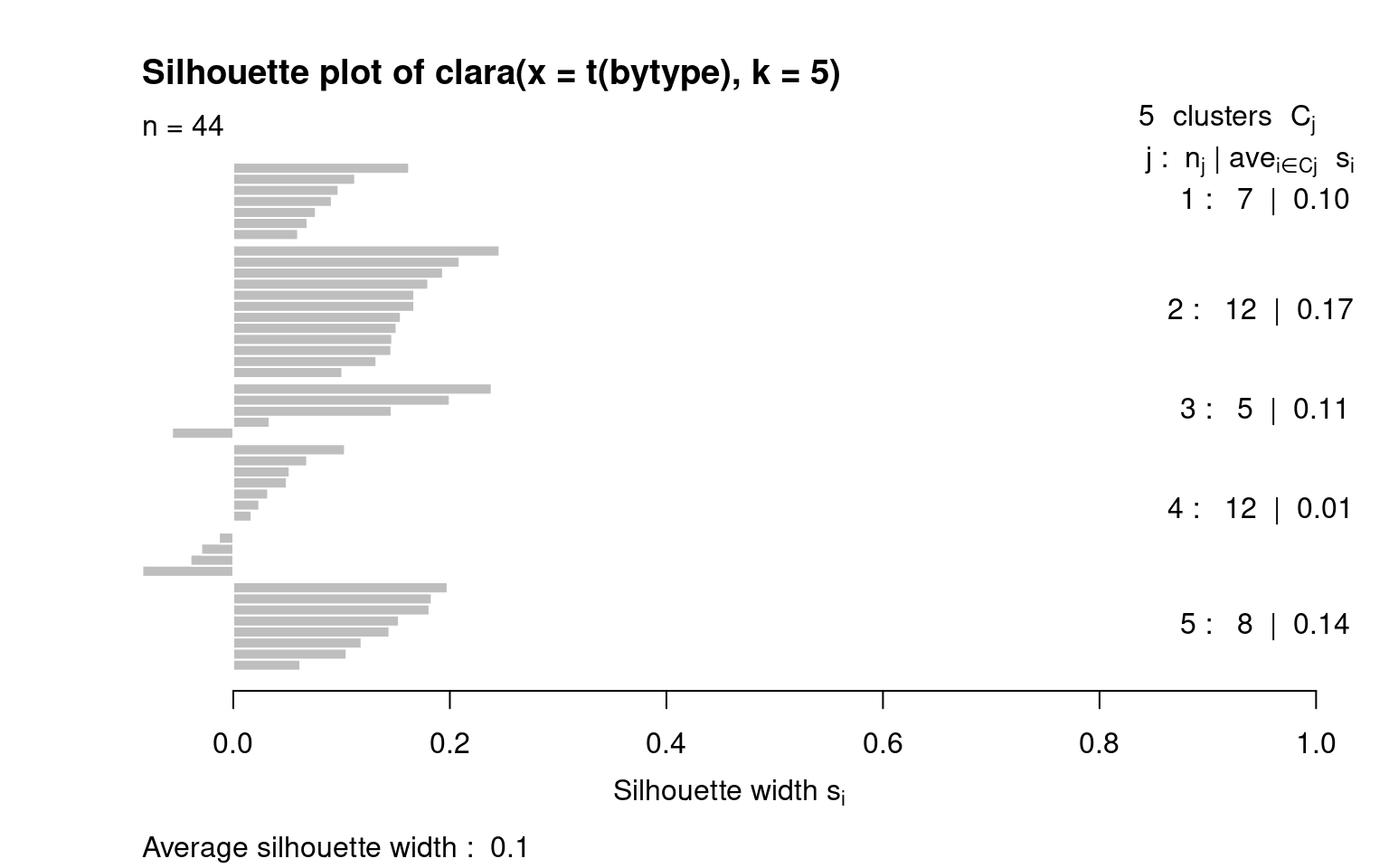
size max_diss av_diss isolation
[1,] 309 10.630146 7.339754 1.796823
[2,] 186 10.862780 7.270657 1.836145
[3,] 235 15.842980 7.571415 2.640497
[4,] 160 11.045361 7.667071 1.425950
[5,] 1 0.000000 0.000000 0.000000
[6,] 50 9.899495 7.437426 1.459601
[7,] 76 9.591663 7.397349 1.208436This suggests that although the big-5 defines up to 2^5=32 personality types, most people fall into just a few (4-5) personality clusters. The largest, group-1, has 323 people in it, which is about 1/3 of the data. If we look at the mediod, it is a set of answers across the entire data survey:
Each series is a person who best describes one group, across the 44 questions of the survey.
Cluster by question:
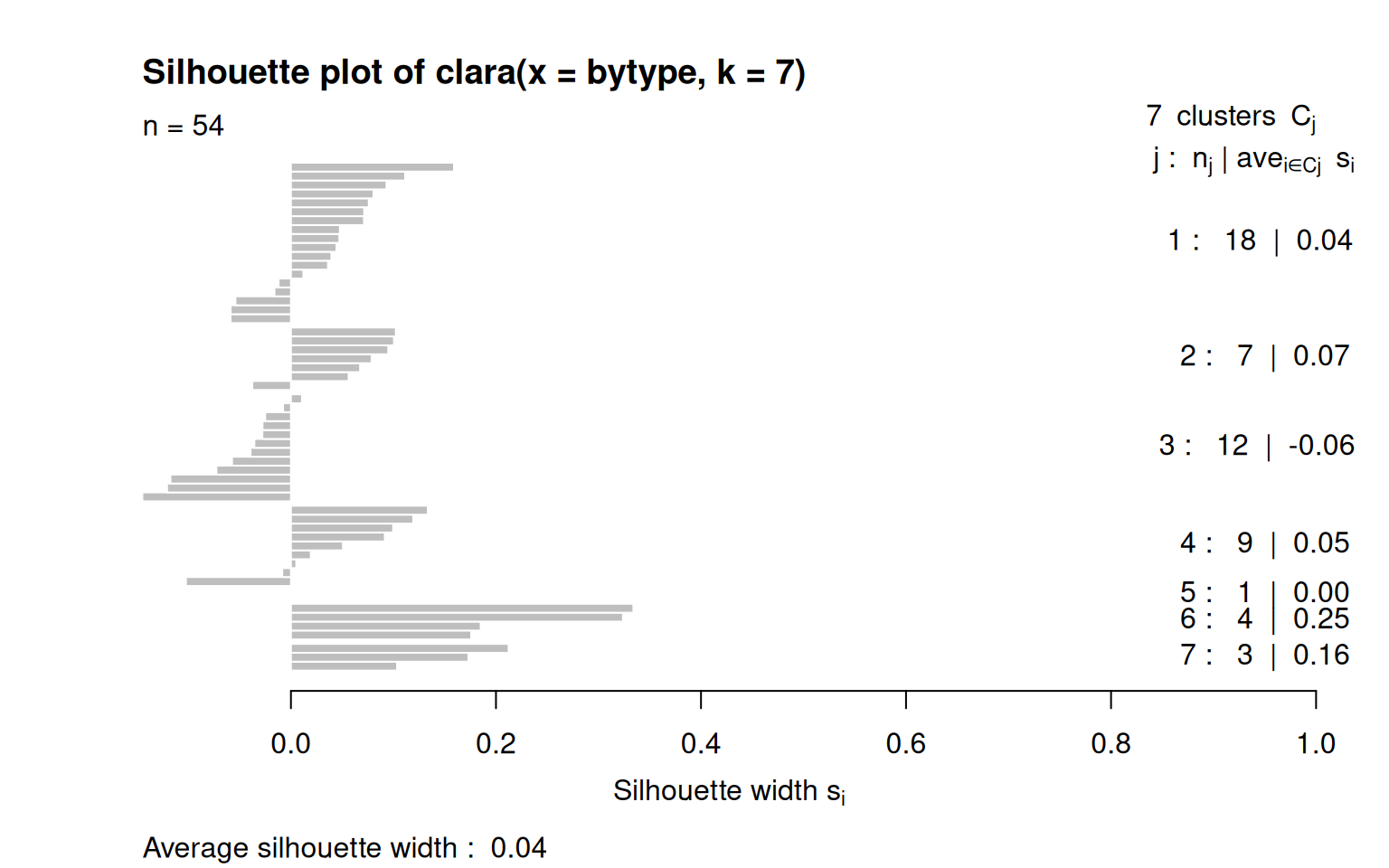
Since there were five cluster types, maybe we can use this to cluster by question. We will use clara again, although now there are 1000+ features and 44 items.
c2 <- clara(t(bytype), k = 5)
for (i in 1:5) {
cat(paste("Group ", i, ": \n", sep = ""))
print(c2$clustering[c2$clustering == i])
}Group 1:
A1 A6 A8 C11 C13 C14 C18
1 1 1 1 1 1 1
Group 2:
A2 A3 A4 A5 A7 A9 C10 C12 C15 C16 C17 O36
2 2 2 2 2 2 2 2 2 2 2 2
Group 3:
E19 E20 E23 E25 O41
3 3 3 3 3
Group 4:
E21 E22 E24 E26 O35 O37 O38 O39 O40 O42 O43 O44
4 4 4 4 4 4 4 4 4 4 4 4
Group 5:
N27 N28 N29 N30 N31 N32 N33 N34
5 5 5 5 5 5 5 5 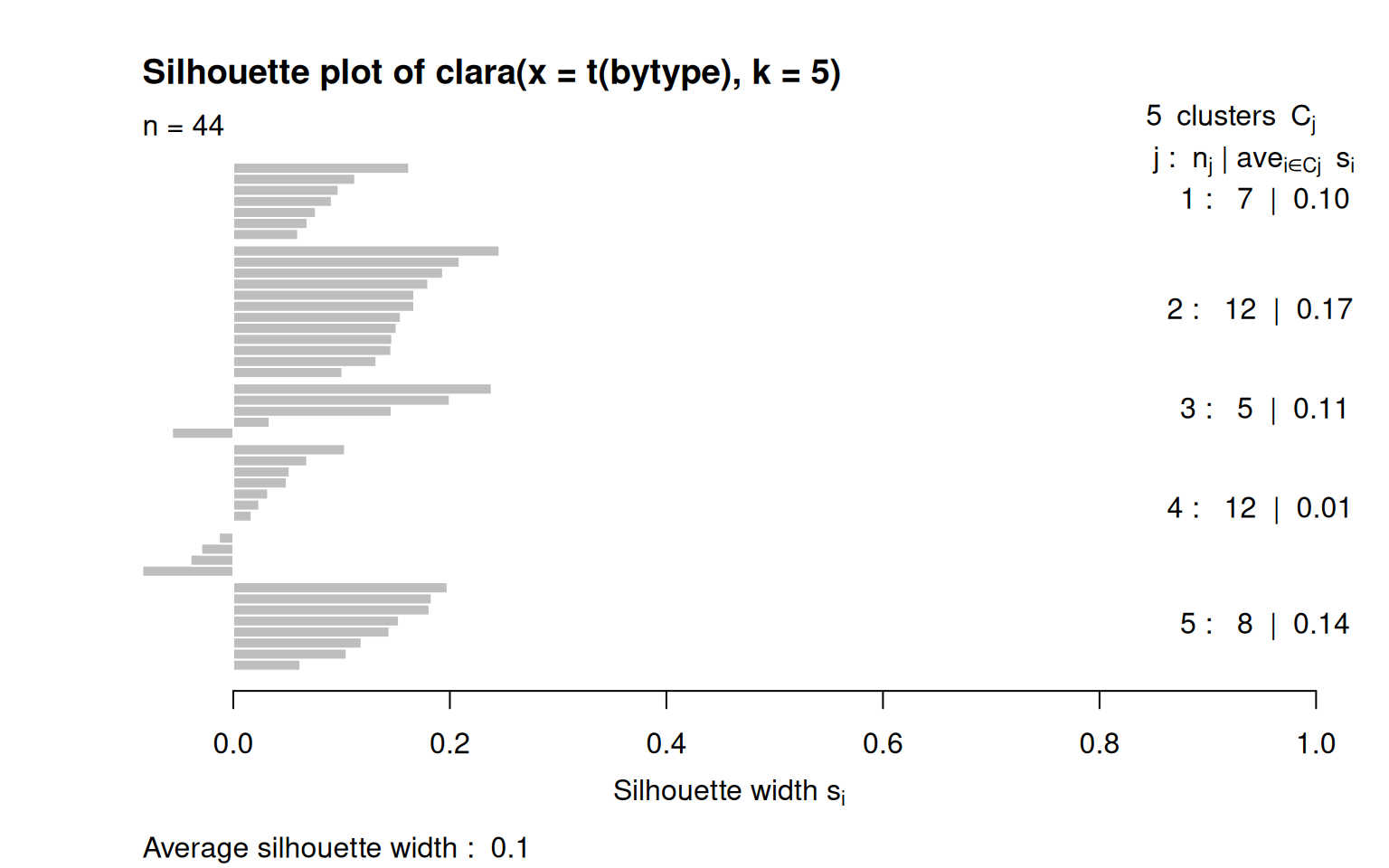
[1] "Cluster membership by personality dimension:"
1 2 3 4 5
A 3 6 0 0 0
C 4 5 0 0 0
E 0 0 4 4 0
N 0 0 0 0 8
O 0 1 1 8 0Notice that the clusters it picked out were not exactly the 5-dimensions. Part of this may be because of reversed-framed items might not be exactly symmetric with positively-framed questions, but it does suggest that the personality story seems to depend on the method we use to analyze the data.
Summary of Classic clustering techniques
Let’s summarize the classic clustering techniques we have covered so
far. We have covered two general approaches to clustering: hierarchical
and finite clustering. Hierarchical clustering is a bottom-up approach
that builds a tree of clusters, and can be either agglomerative or
divisive. Agglomerative methods start with each item as a cluster, and
then merge the closest pairs of clusters together, until all items are
in one cluster. Divisive methods start with all items in one cluster,
and then divide the cluster into two, and then divide those into two,
and so on. The cluster library provides a number of methods for
hierarchical clustering, including agnes and
diana. These methods require a distance matrix, and can be
used to find a complete tree of clusters. The cluster
library also provides a number of methods for finite clustering,
including k-means, fanny, and PAM. These methods require raw data, and
provide a fixed number of clusters.