Return to course site

Mixture Modeling: Mixture of Regressions

Mixture Modeling

Mixture Modeling

A mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs. We previously used a very simple model–where each variable is defined by its mean and standard deviation, to do model-based clustering. But mixture modeling permits finding mixtures of hidden group memberships for other kinds of models, including regression models. This sometimes enables you to identify sets of distinct relationships amongst sub-groups, hidden within a larger population. The goal of mixture modeling is to model your data as a mixture of processes or populations that have distinct patterns of data.

Example 1: Two linear models

Suppose we have two types of people: those who like romantic comedy movies, and those who hate romantic comedies. On a movie rating site, we have measured ratings of anonymous people rating how much they like movies, that we have already measured on hotw romantic they are. Thus, we’d expect a crossing pattern in the data, like we see below. If we knew why type of person each person was, we’d be able to fit separate regression models, but we don’t.

set.seed(100)
x1 <- rnorm(1000) * 50
x2 <- rnorm(1000) * 50
y1 <- x1 * 3 + 10 + rnorm(1000) * 30
y2 <- -3 * x2 + 25 + rnorm(1000) * 50
x <- c(x1, x2)
y <- c(y1, y2)
par(mfrow = c(1, 3))
plot(x1, y1)
plot(x2, y2)
plot(x, y)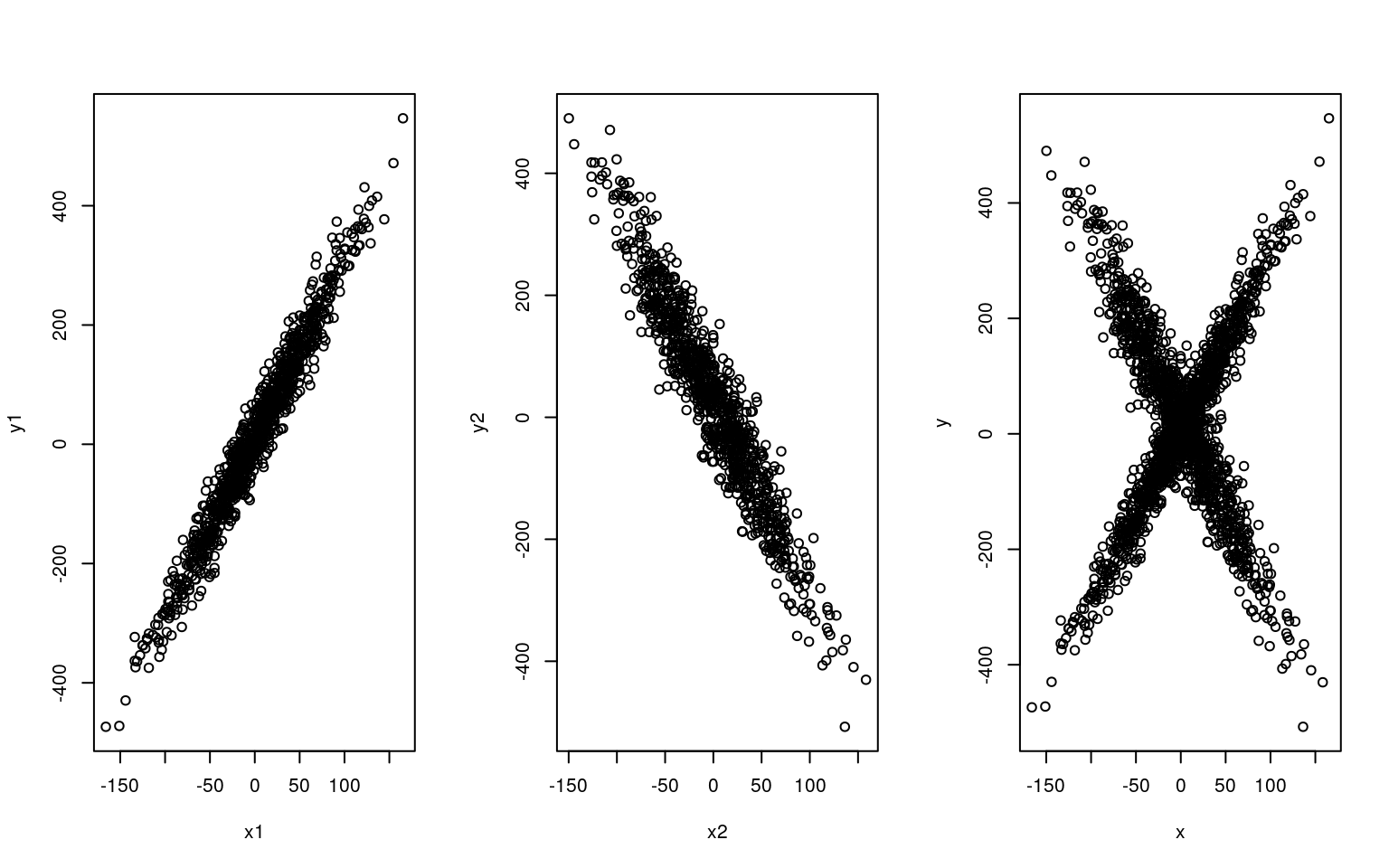

lm(y1 ~ x1)


Call:
lm(formula = y1 ~ x1)

Coefficients:
(Intercept)           x1
      9.573        2.976

lm(y2 ~ x2)


Call:
lm(formula = y2 ~ x2)

Coefficients:
(Intercept)           x2
     25.196       -3.097

If we try to fit data by using a single linear regression, we fail:

plot(x, y)
lm1 <- lm(y ~ x)
summary(lm1)


Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max
-537.79 -102.55    1.96  102.96  513.75

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.26748    3.53271   5.171 2.56e-07 ***
x            0.08846    0.07026   1.259    0.208
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 158 on 1998 degrees of freedom
Multiple R-squared:  0.0007929, Adjusted R-squared:  0.0002928
F-statistic: 1.586 on 1 and 1998 DF,  p-value: 0.2081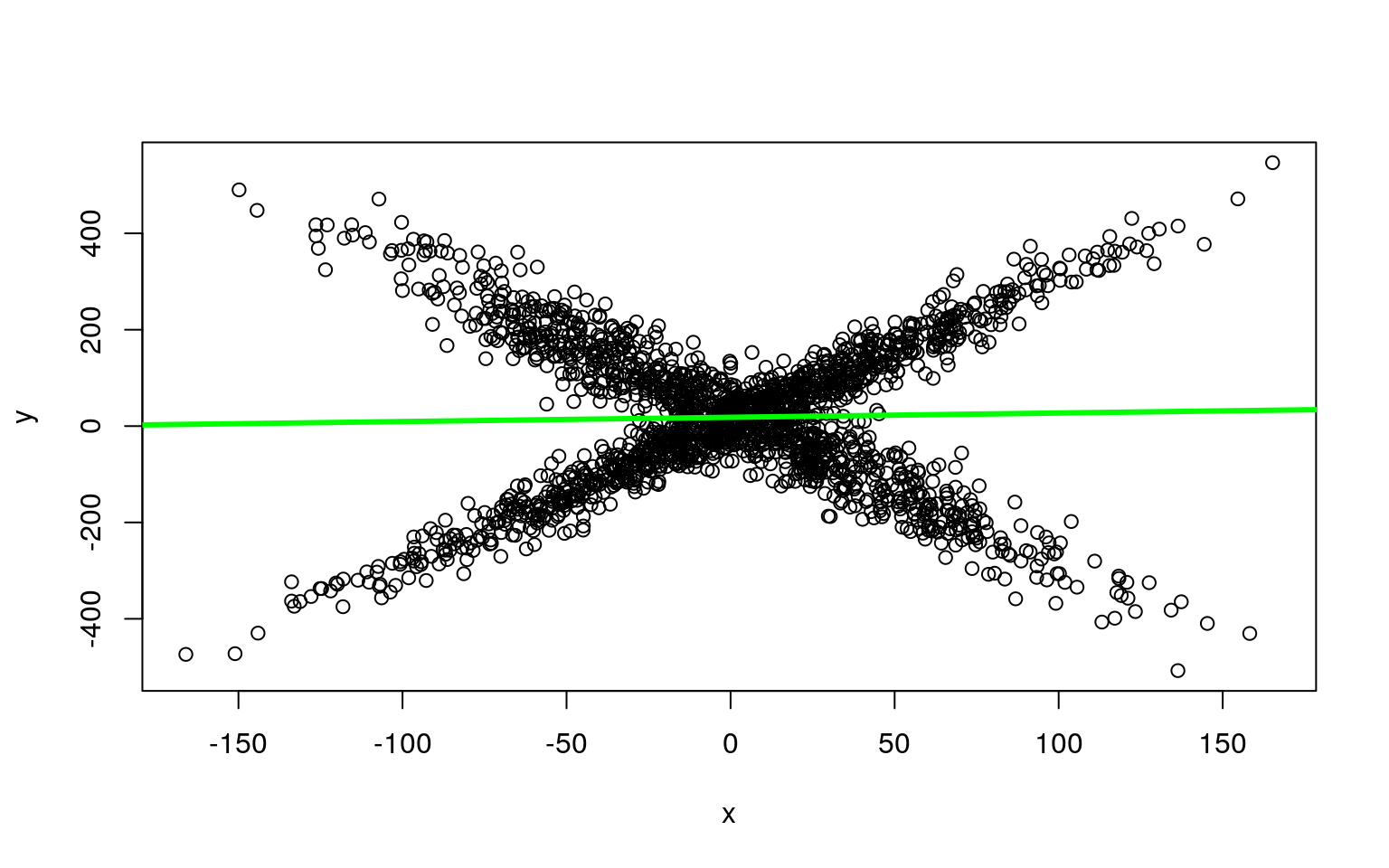

abline(lm1$coefficients, col = "green", lwd = 3)

And from summary(lm1), R-squared = 0.0008135

summary(lm1)


Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max
-537.79 -102.55    1.96  102.96  513.75

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.26748    3.53271   5.171 2.56e-07 ***
x            0.08846    0.07026   1.259    0.208
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 158 on 1998 degrees of freedom
Multiple R-squared:  0.0007929, Adjusted R-squared:  0.0002928
F-statistic: 1.586 on 1 and 1998 DF,  p-value: 0.2081

Fitting mixtures of regressions using E-M and flexmix

If we could use the same approach as with clustering, but instead of gaussians around means, we might have each sub-group defined by a linear model. In this case, as long as we can produce a likelihood estimate for a model, we can use the E-M algorithm to identify and estimate the groups. That is, we can fit a model to a subgroup, obtain the maximum likelihood estimate, then place each observation in the model it is best described by, and repeat until things settle down.

To review: E-M stands for Expectation-Maximization. It is an iterative process whereby you apply two complementary processes. Suppose you assume there are two sub-groups. First, randomly assign members to either of the sub-groups. Next, you compute a maximum likelihood (ML) estimate for each sub-group. Now, because of random variation, there are likely to be members of one group that are better described by the other group (in terms of likelihood). You then apply the ‘maximization’ step to re-sort data into the group that better describes them. You repeat this process, re-estimating your models and re-sorting members until nobody is better described by a model that they are not in. Original research on the E-M algorithm proved that it would converge to a local maximum; you might not get the global maximum however, so you typically repeat the process many times and pick the best outcome you find.

This is possible to do by hand, and in this case is not too complicated.

split <- rep(1:2, 1000)

plot(x, y, col = split)

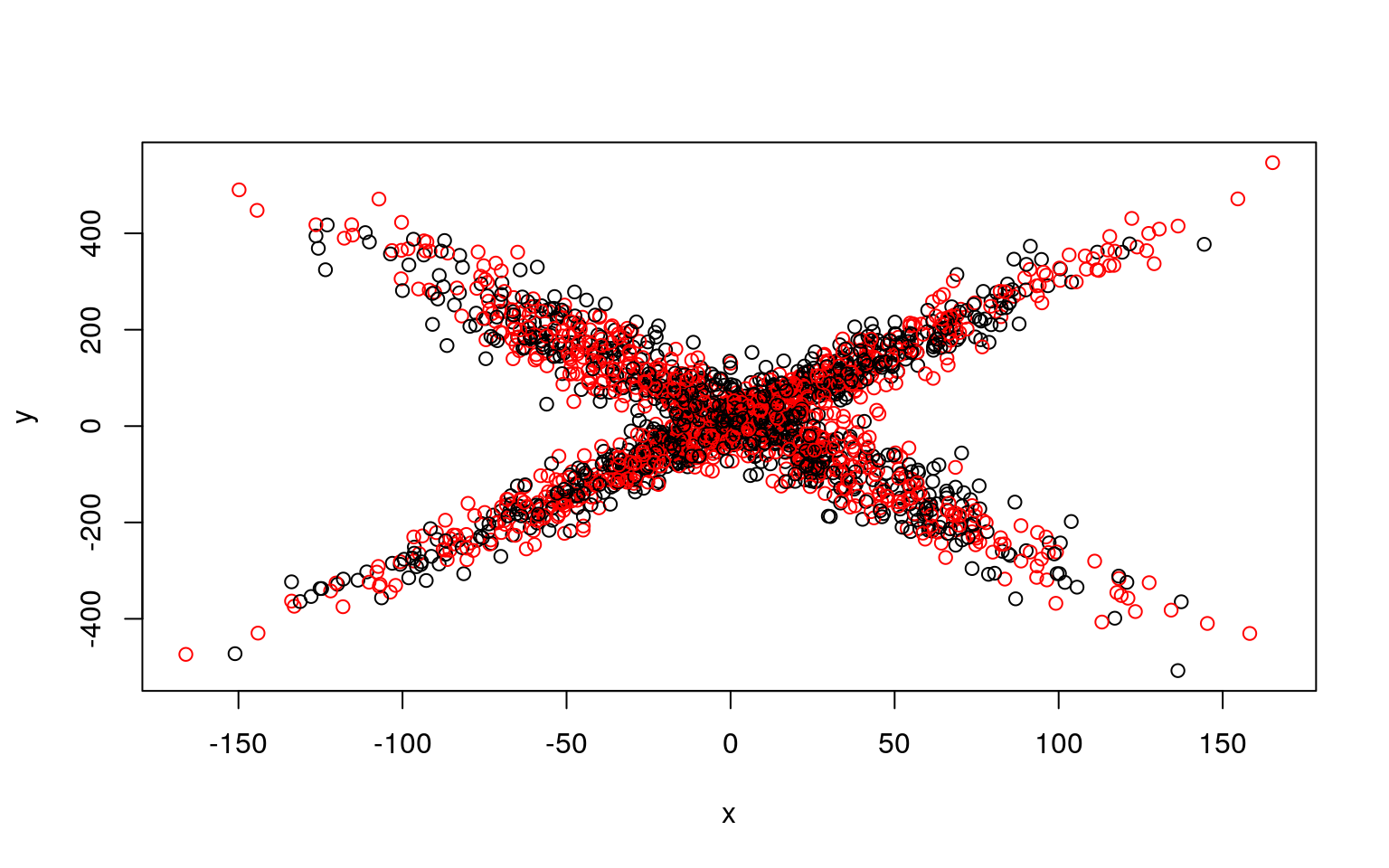
for (i in 1:5) {
    
    lm1 <- glm(y[split == 1] ~ x[split == 1])
    lm2 <- glm(y[split == 2] ~ x[split == 2])
    
    
    
    ## Compute residuals of all the data for the two models
    res1 <- (predict(lm1, data.frame(x)) - y)
    res2 <- (predict(lm2, data.frame(x)) - y)
    
    likelihood <- cbind(dnorm(res1, mean = 0, sd = sd(res1)), dnorm(res2, mean = 0, 
        sd = sd(res2)))
    
    split <- apply(likelihood, 1, which.max)
    plot(x, y, col = split, main = i)
    print(lm1)
    print(lm2)
    
}


Call:  glm(formula = y[split == 1] ~ x[split == 1])

Coefficients:
  (Intercept)  x[split == 1]
     17.09494        0.08062

Degrees of Freedom: 999 Total (i.e. Null);  998 Residual
Null Deviance:      23240000
Residual Deviance: 23220000     AIC: 12900

Call:  glm(formula = y[split == 2] ~ x[split == 2])

Coefficients:
  (Intercept)  x[split == 2]
     19.43532        0.09495

Degrees of Freedom: 999 Total (i.e. Null);  998 Residual
Null Deviance:      26660000
Residual Deviance: 26640000     AIC: 13030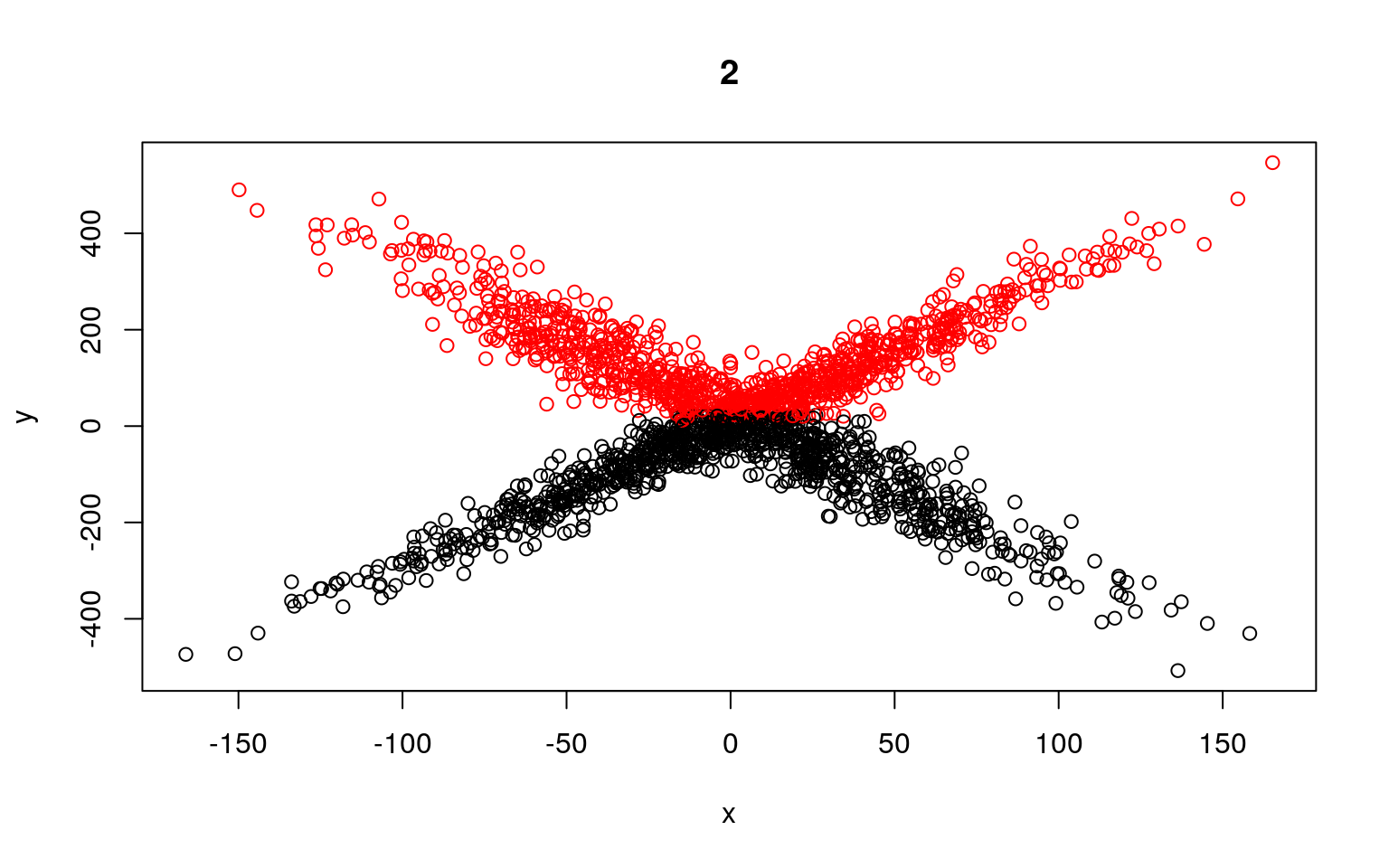


Call:  glm(formula = y[split == 1] ~ x[split == 1])

Coefficients:
  (Intercept)  x[split == 1]
     -14.6458         0.2283

Degrees of Freedom: 1058 Total (i.e. Null);  1057 Residual
Null Deviance:      23420000
Residual Deviance: 23290000     AIC: 13600

Call:  glm(formula = y[split == 2] ~ x[split == 2])

Coefficients:
  (Intercept)  x[split == 2]
     54.99022       -0.01926

Degrees of Freedom: 940 Total (i.e. Null);  939 Residual
Null Deviance:      24090000
Residual Deviance: 24090000     AIC: 12230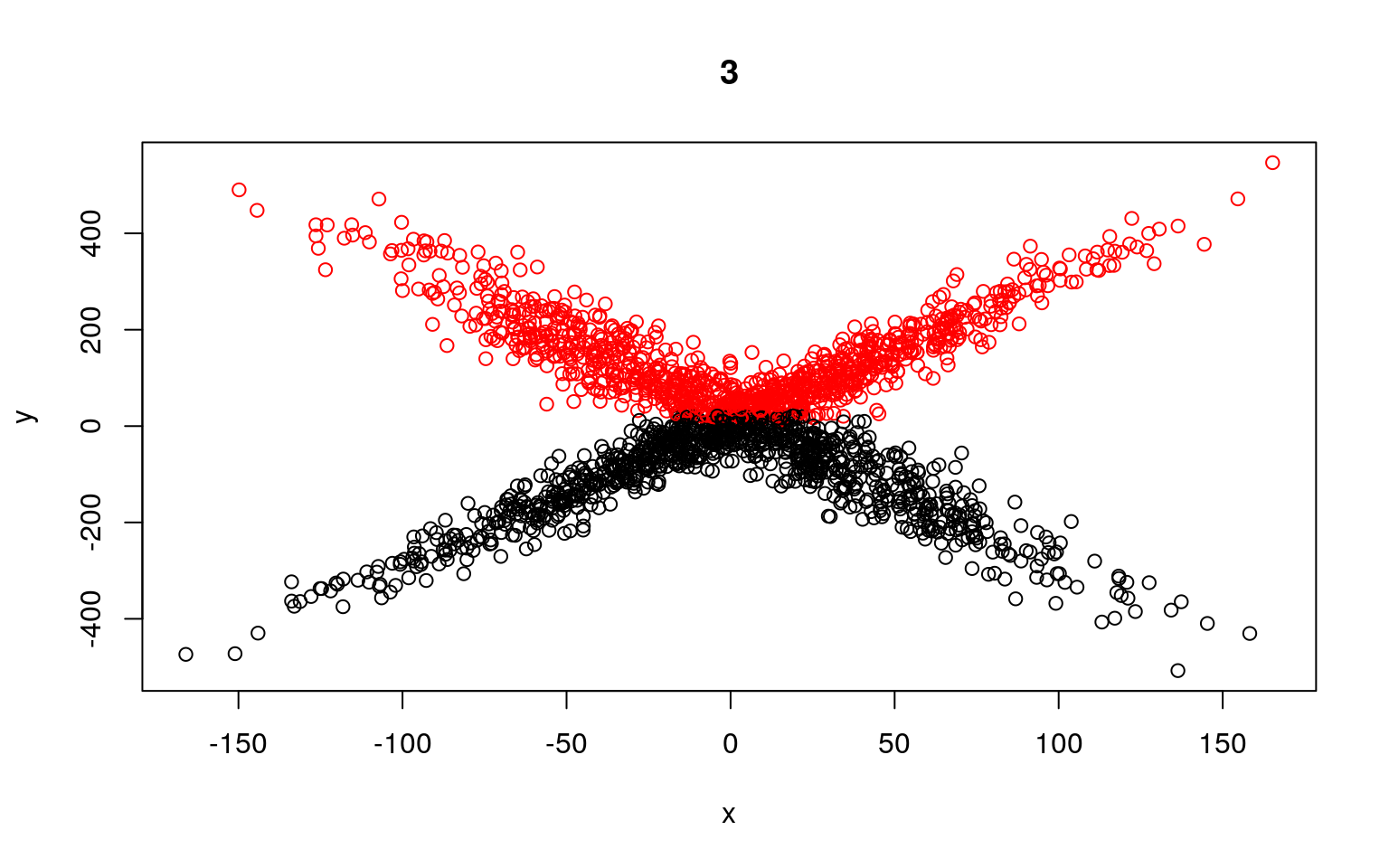


Call:  glm(formula = y[split == 1] ~ x[split == 1])

Coefficients:
  (Intercept)  x[split == 1]
    -107.3808         0.1218

Degrees of Freedom: 997 Total (i.e. Null);  996 Residual
Null Deviance:      9401000
Residual Deviance: 9364000  AIC: 11970

Call:  glm(formula = y[split == 2] ~ x[split == 2])

Coefficients:
  (Intercept)  x[split == 2]
    143.75711       -0.07905

Degrees of Freedom: 1001 Total (i.e. Null);  1000 Residual
Null Deviance:      8980000
Residual Deviance: 8964000  AIC: 11970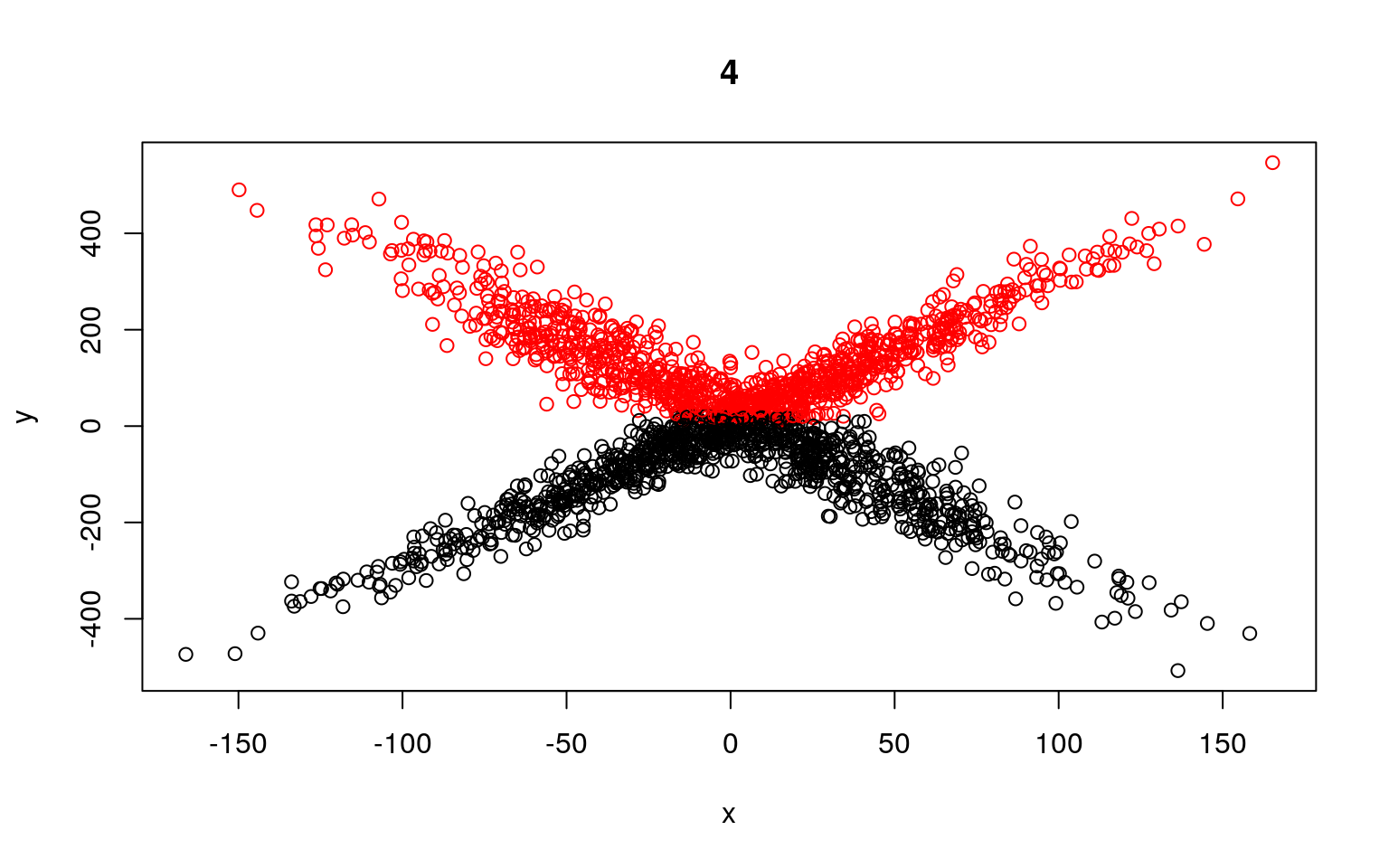


Call:  glm(formula = y[split == 1] ~ x[split == 1])

Coefficients:
  (Intercept)  x[split == 1]
    -109.0668         0.1154

Degrees of Freedom: 984 Total (i.e. Null);  983 Residual
Null Deviance:      9183000
Residual Deviance: 9150000  AIC: 11800

Call:  glm(formula = y[split == 2] ~ x[split == 2])

Coefficients:
  (Intercept)  x[split == 2]
    142.20347       -0.08373

Degrees of Freedom: 1014 Total (i.e. Null);  1013 Residual
Null Deviance:      9173000
Residual Deviance: 9155000  AIC: 12130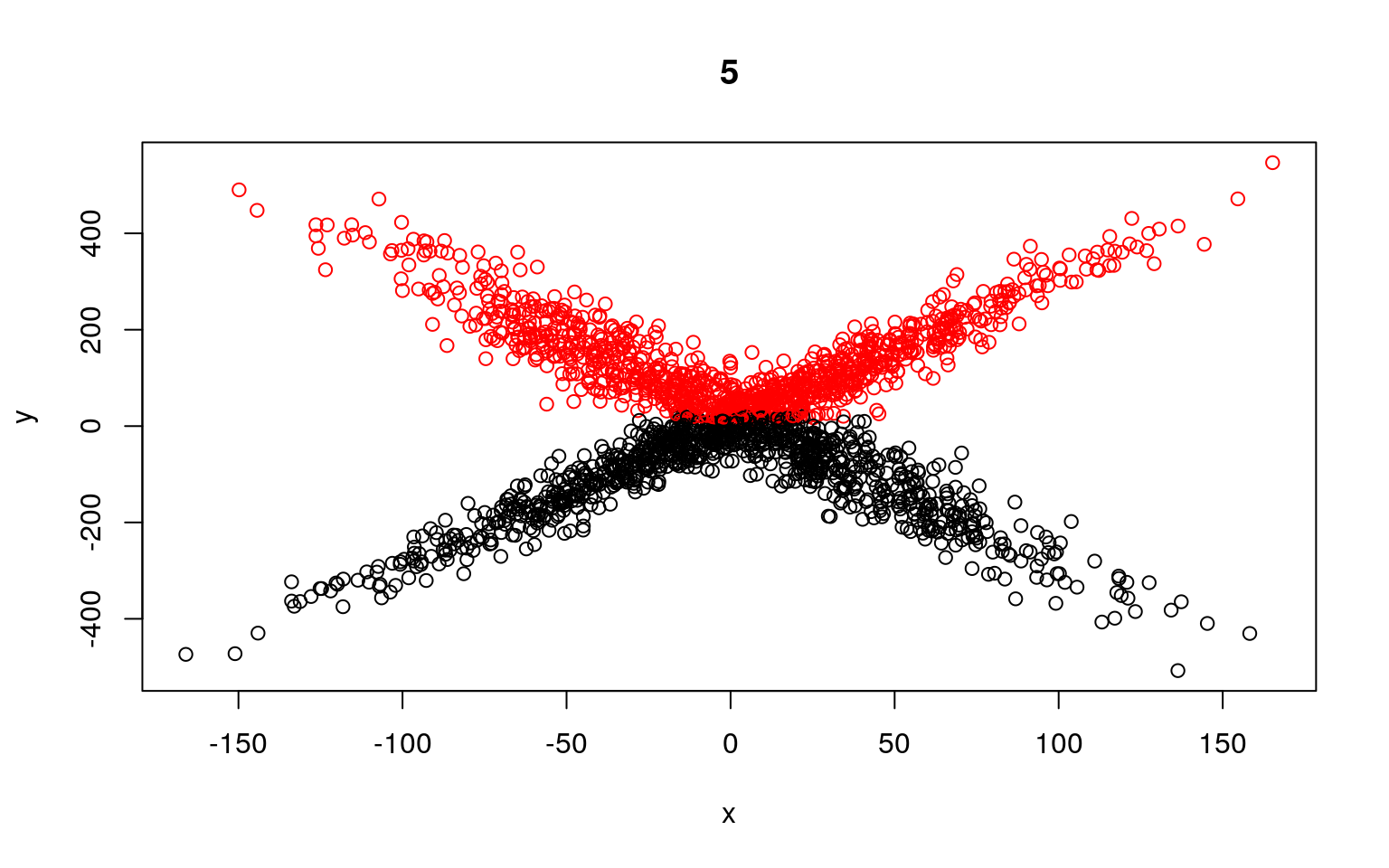


Call:  glm(formula = y[split == 1] ~ x[split == 1])

Coefficients:
  (Intercept)  x[split == 1]
     -110.747          0.109

Degrees of Freedom: 971 Total (i.e. Null);  970 Residual
Null Deviance:      8973000
Residual Deviance: 8944000  AIC: 11640

Call:  glm(formula = y[split == 2] ~ x[split == 2])

Coefficients:
  (Intercept)  x[split == 2]
    140.63808       -0.08789

Degrees of Freedom: 1027 Total (i.e. Null);  1026 Residual
Null Deviance:      9374000
Residual Deviance: 9354000  AIC: 12290

We can see that the two models typically found have low slope, and a difference in the intercept. But the two models are not that great; if we happened upon a pair of models that crossed, the solution would be better. We might have to run a few dozen or hundreds of times to find that one. The flexmix library automates this al for us.

Flexmix modeling:

The ‘flexmix’ package allows us to do this very easily. FlexMix implements a general framework for fitting discrete mixtures of regression models in the R statistical computing environment.

library(flexmix)
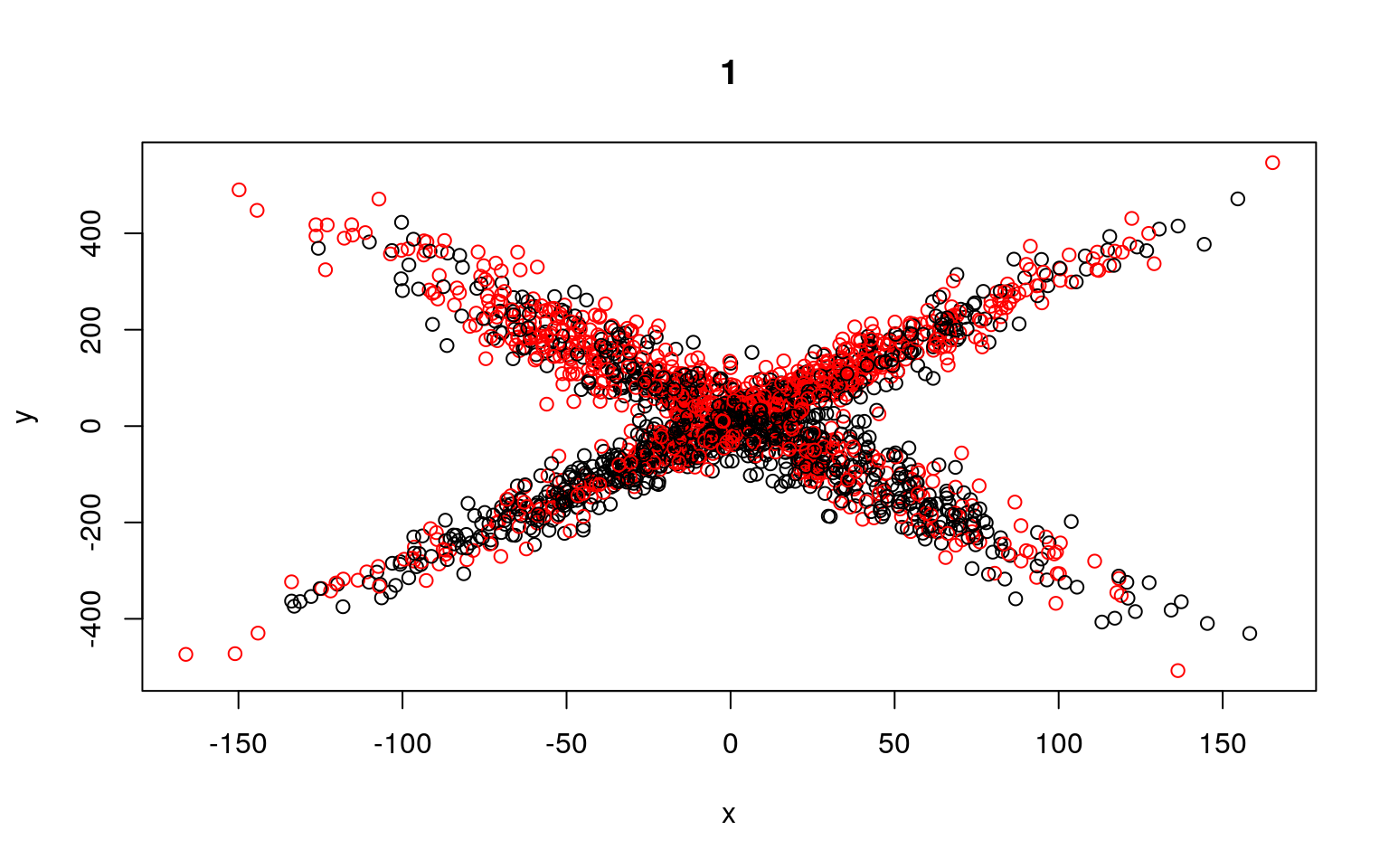
model <- flexmix(y ~ x, k = 2)
plot(x, y, col = clusters(model))
abline(parameters(model)[1:2, 1], col = "blue", lwd = 3)
abline(parameters(model)[1:2, 2], col = "green", lwd = 3)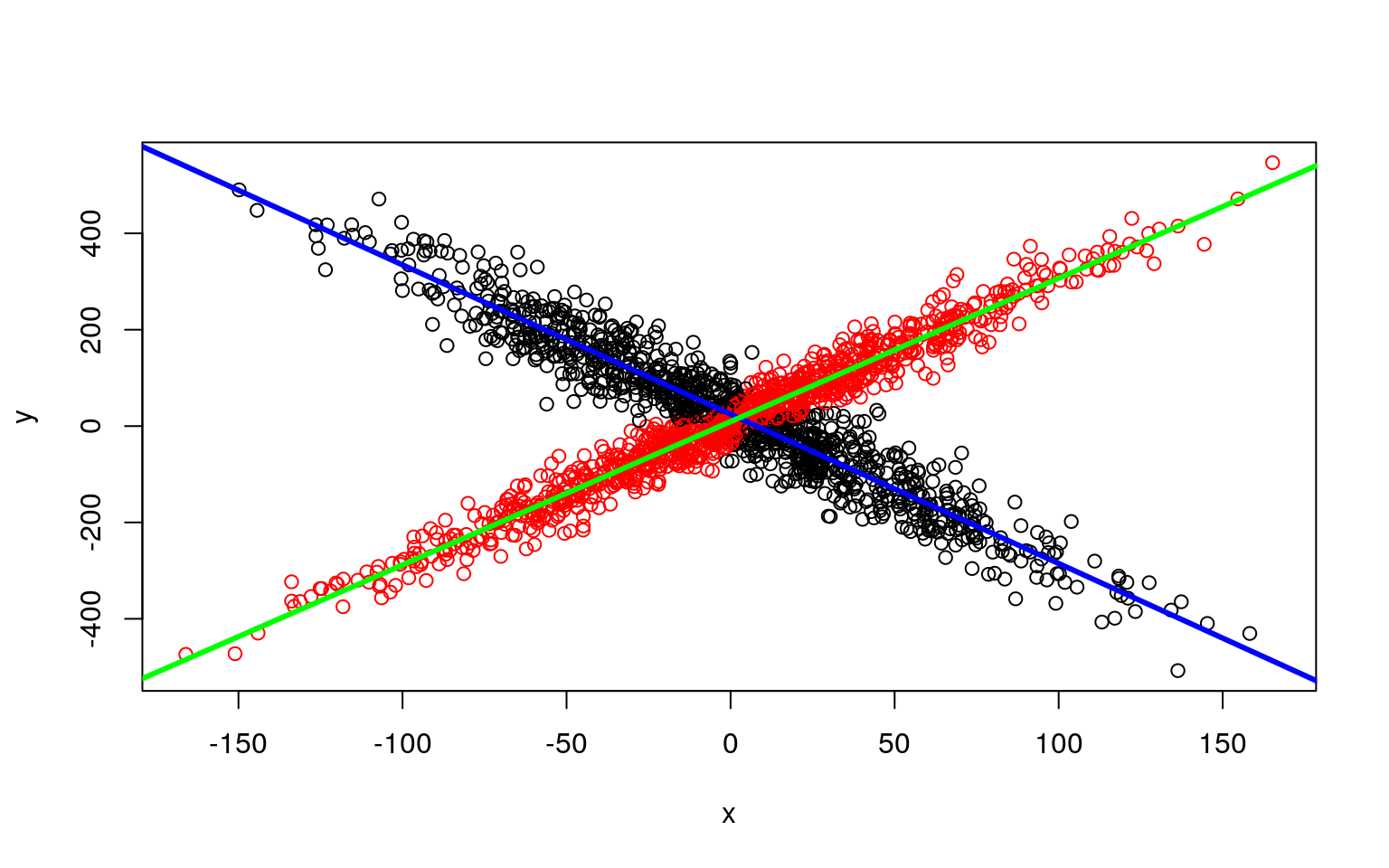

Along with being easier to use, it gets the original (crossing) model right almost every time–there are other heuristics used for model search that help the flexmix model get a better solution than we get when building by hand.

The summary() method gives the estimated prior probabilities, the number of observations assigned to the corresponding clusters, the number of observations where posterior probability > \(\delta\) for each component (with a default of .0001). This indicates the proportion and number of observations that are fit even a little bit by the model, in comparison to those fit best by the model. In the above example, one component has a ratio of around .78–there were 1375 points that had non-zero likelihood of being in that group, and of those 78% were best fit by that group. The distribution of those likelihoods is shown as a rootogram (with the count scale is transformed). Histograms or rootograms of the posterior class probabilities can be used to visually assess the cluster structure. Rootograms are very similar to histograms, the only difference is that the height of the bars correspond to square roots of counts rather than the counts themselves, so that low counts are more visible and peaks less so.

summary(model)


Call:
flexmix(formula = y ~ x, k = 2)

       prior size post>0 ratio
Comp.1 0.494  933   1501 0.622
Comp.2 0.506 1067   1375 0.776

'log Lik.' -11251.23 (df=7)
AIC: 22516.45   BIC: 22555.66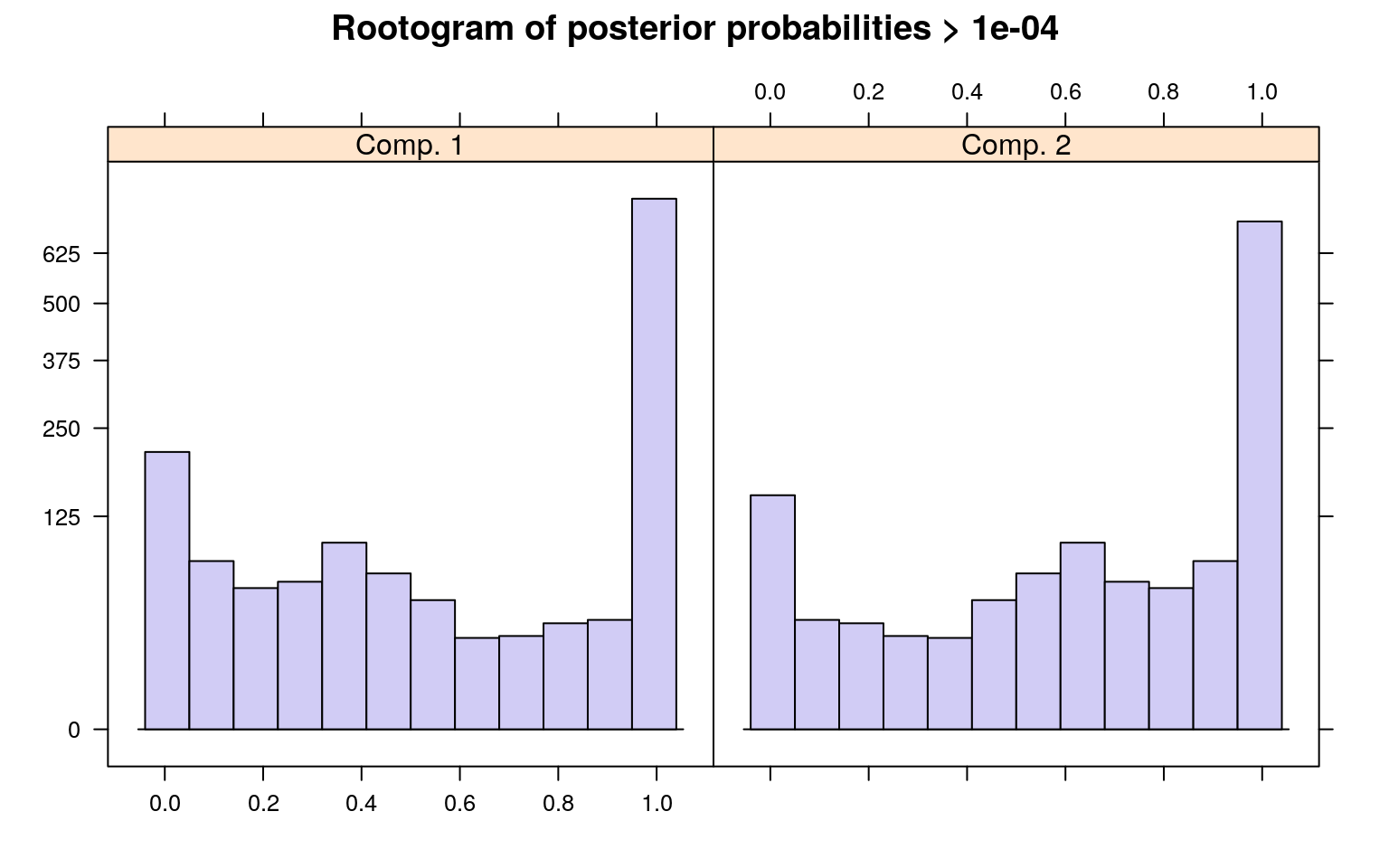

plot(model)

parameters(model)

                    Comp.1    Comp.2
coef.(Intercept) 24.605851  9.315453
coef.x           -3.098168  2.974608
sigma            47.836606 31.959836

When interpreting rootograms, keep in mind that there is no ‘ground truth’. A peak near probability 1 indicates that many of the points are overwhelmingly well-represented by that cluster. A peak near 0 would indicate that many points clearly don’t fit the category (which is also usually good). Points in the middle indicate a lack of separation–there are points that are only moderately well-described by that group, which should be considered with respect to the number of groups you think exist.

Example: A mixture of variances

Mixture modeling can be used to identify outliers or select elements that are caused by the same process but have mutch larger variance. Sometimes, skewed distributions with long tails are modeled as mixtures of two gaussians–one to capture the fairly symmetrical centroid of the distribution, and a second to capture the long tail. At the end of the day, you may treat the tail as a nuisance and use the centroid model as the one you care about.

Random 1000 variables for x and y

x1 <- rep(1:10, 50)
x2 <- rep(1:10, each = 5)
y1 <- 3 * x1 + 10 + rnorm(500) * 3
y2 <- 3 * x2 + 10 + rnorm(50) * 50
x <- c(x1, x2)
y <- c(y1, y2)
plot(x, y)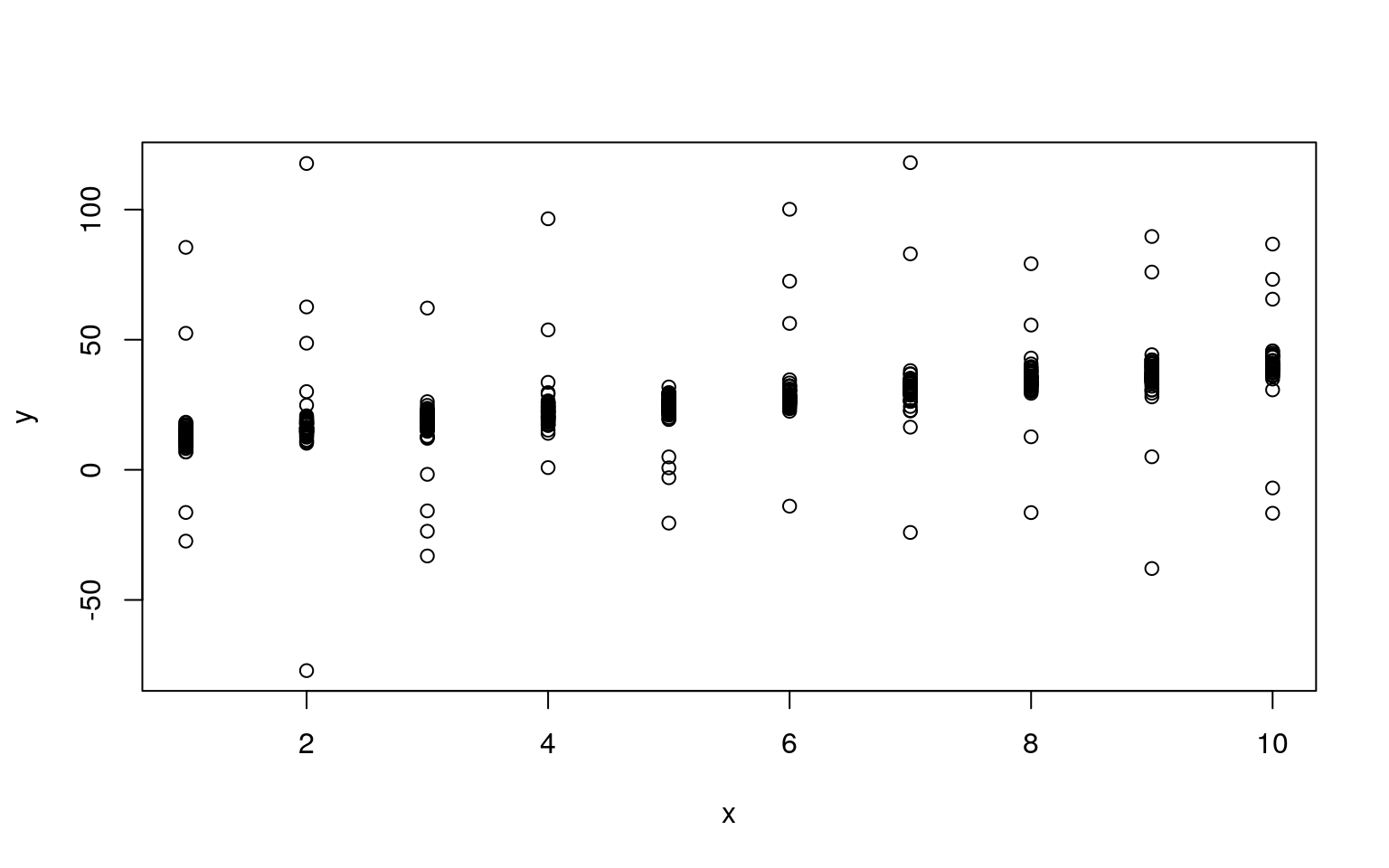

Notice that we have a clear linear relationship, along with a handful of outliers. For a regular maxmimum-likelihood model, these outliers present a problem because they are either very unlikely (punishing the model), or the model’s variance must get larger to make them reasonable, making all the other data less likely.

library(flexmix)
model2a <- flexmix(y ~ x, k = 1)
summary(model2a)


Call:
flexmix(formula = y ~ x, k = 1)

       prior size post>0 ratio
Comp.1     1  550    550     1

'log Lik.' -2222.624 (df=3)
AIC: 4451.247   BIC: 4464.177

model2b <- flexmix(y ~ x, k = 2)
summary(model2b)


Call:
flexmix(formula = y ~ x, k = 2)

        prior size post>0  ratio
Comp.1 0.0976   45    550 0.0818
Comp.2 0.9024  505    510 0.9902

'log Lik.' -1639.939 (df=7)
AIC: 3293.877   BIC: 3324.047

parameters(model2b)

                    Comp.1   Comp.2
coef.(Intercept) 16.905170 9.983649
coef.x            2.298848 3.015417
sigma            43.087887 2.872276

clusters(model2b)

 [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[36] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[71] 2 2 2 2 2
 [ reached getOption("max.print") -- omitted 475 entries ]

In this case, the 2-group model will often select 40/50 of the outliers to be in the secondary group. We’d like to know whether the 2-group solution is any better? We can use a criterion such as BIC to do this.

Bayesian Information Criterion (BIC)

The BIC is a statistic that is based on both the likelihood of the data AND a punishing factor related to the number of parameters used. If you have three parameters for a default model (intercept, slope, and variance), you would have six for a model with two clusters, and nine for one with three. To use the BIC statistic, you can just compare across models and determine which is the smallest. This model provides the best trade-off between accuracy and complexity. However, sometimes the differences are small and you still may prefer a more complex model for other reasons.

In the above example, the BIC is given as part of the output of each model, or we can get it directly:

BIC(model2a)

[1] 4464.177

BIC(model2b)

[1] 3324.047

Here, model2b has a much smaller BIC, so we would prefer this one–the two-group model. We’d like to be able to automate this, looking across a number of options; we’d also like to run this many times (and with more than just 2 groups) and see if there are any better soluetions. Here is a way to do both. In the stepFlexmix function, it allows you to specify the numbers of clusters to test, and the number of repetitions at each configuration. We can then select the one with the smallest BIC using the getModel() function

models <- stepFlexmix(y ~ x, k = 1:5, nrep = 10)

1 : * * * * * * * * * *
2 : * * * * * * * * * *
3 : * * * * * * * * * *
4 : * * * * * * * * * *
5 : * * * * * * * * * *

models


Call:
stepFlexmix(y ~ x, k = 1:5, nrep = 10)

  iter converged k k0    logLik      AIC      BIC      ICL
1    2      TRUE 1  1 -2222.624 4451.247 4464.177 4464.177
2   12      TRUE 2  2 -1639.939 3293.877 3324.047 3346.959
3  184      TRUE 3  3 -1636.292 3294.584 3341.993 3643.426
4  169      TRUE 4  4 -1635.737 3301.473 3366.122 3929.523
5  200     FALSE 5  5 -1635.317 3308.633 3390.522 4309.965

summary(models)

     Length       Class        Mode
          1 stepFlexmix          S4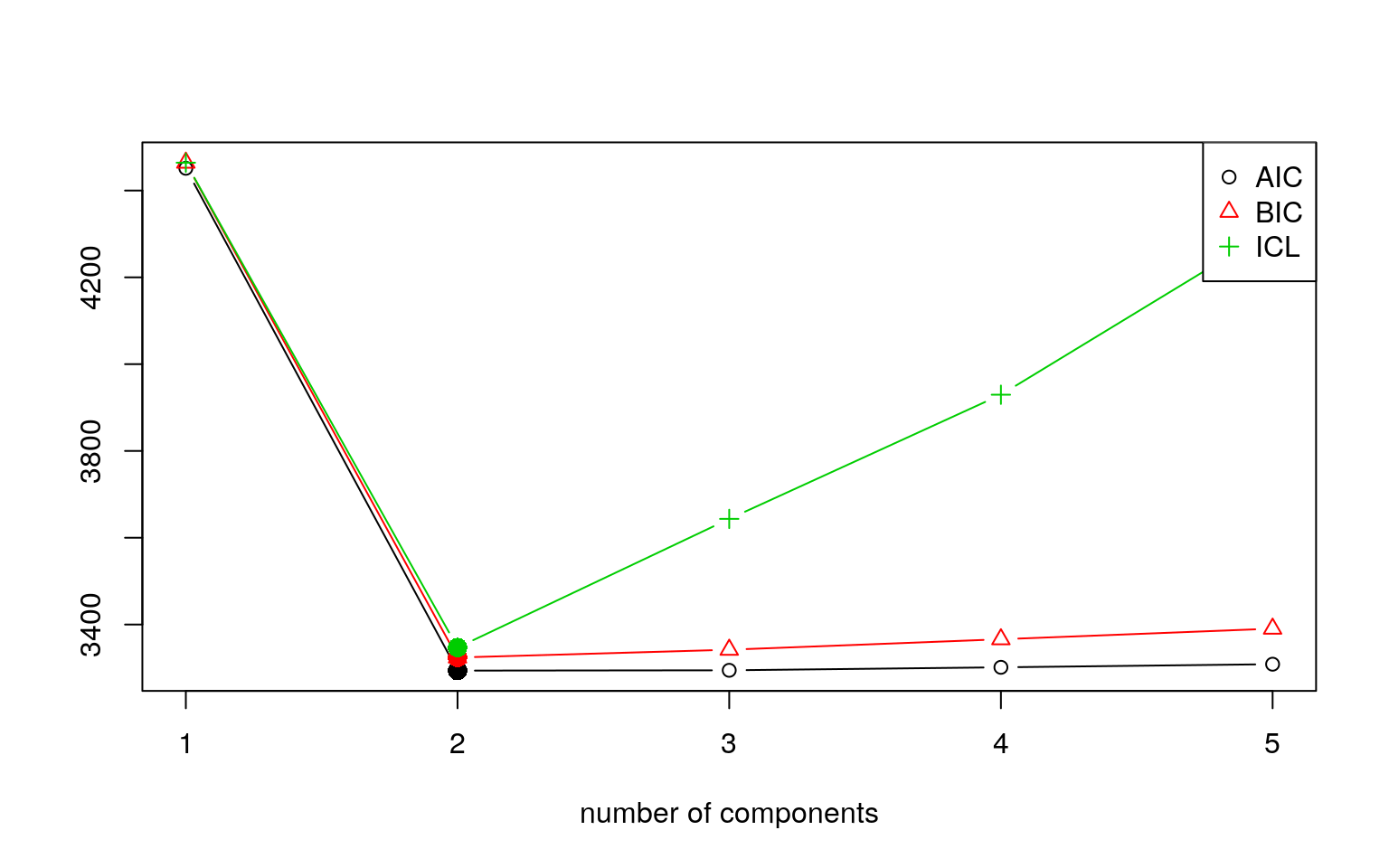

plot(models)

model <- getModel(models, "BIC")
model


Call:
stepFlexmix(y ~ x, k = 2, nrep = 10)

Cluster sizes:
  1   2
 45 505

convergence after 12 iterations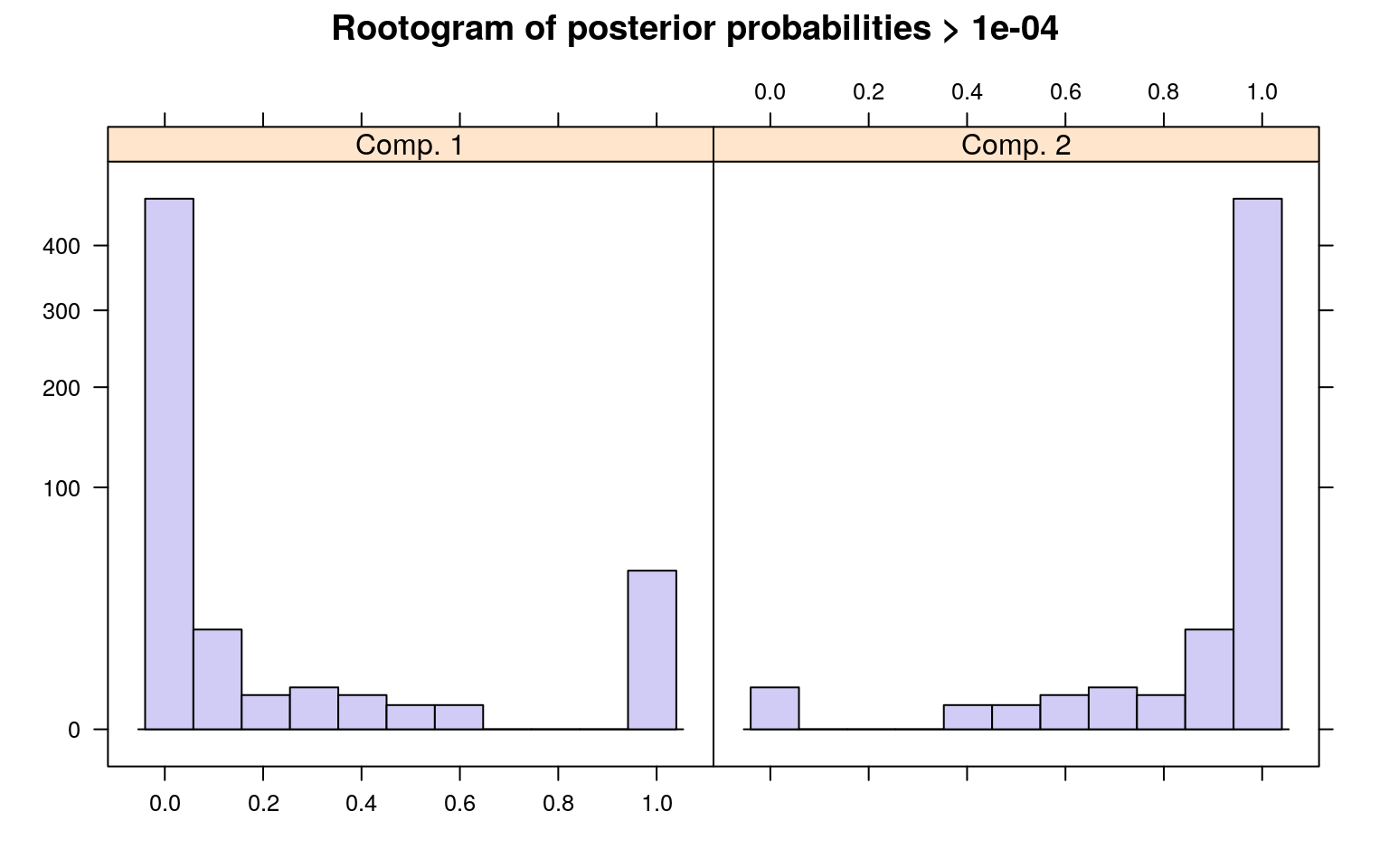

plot(model)

summary(model)


Call:
stepFlexmix(y ~ x, k = 2, nrep = 10)

        prior size post>0  ratio
Comp.1 0.0976   45    550 0.0818
Comp.2 0.9024  505    510 0.9902

'log Lik.' -1639.939 (df=7)
AIC: 3293.877   BIC: 3324.047

parameters(model)

                    Comp.1   Comp.2
coef.(Intercept) 16.906401 9.983737
coef.x            2.298847 3.015395
sigma            43.095174 2.872488

clusters(model)

 [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[36] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[71] 2 2 2 2 2
 [ reached getOption("max.print") -- omitted 475 entries ]

This does pretty well. There are a few things to examine. First, we can look at the post>0 ratio. This sets a very small criterion and asks how many of the data points have likelihood greater than that small level (post>0). It then asks how many are placed in the category based on maximum likelihood. For the larger component, we have a high proportion–almost all of the points that are described by the larger component at all are placed in that category. The second component is less good–almost all of the points could be described by that component, but are just better descibed by the other component. This makes sense in our case, because we have two overlapping distributions. Other times, we might want to have mutually-exclusive clusters.

Note that the model estimates completely different parameters for each group; we’d probably want to just estimate a different variance parameter, and to do that we’d need either to do this by hand or use another flexmix model (possibly a custom model)–it might not even be possible.

Example: learners and non-learners

In this example, suppose that you have tested a group of people repeatedly. Maybe, some people get fatigued in this situation, and so their data get worse over time; another group learn and so their data get better over time. On average, the performance may be flat, but this could hide two separate groups. But these groups might not be labeled, and they may not be easily detectable.

learners <- t(matrix(5 + 0.5 * (1:10) + 1.5 * rnorm(100), 10))
fatigues <- t(matrix(10 - 0.5 * (1:10) + 1.5 * rnorm(100), 10))
data <- rbind(learners, fatigues)
par(mfrow = c(1, 3))
matplot(t(learners), pch = 16, col = "black", main = "Learners")
matplot(t(fatigues), pch = 16, col = "black", main = "Fatigued")
matplot(t(data), pch = 16, col = "black")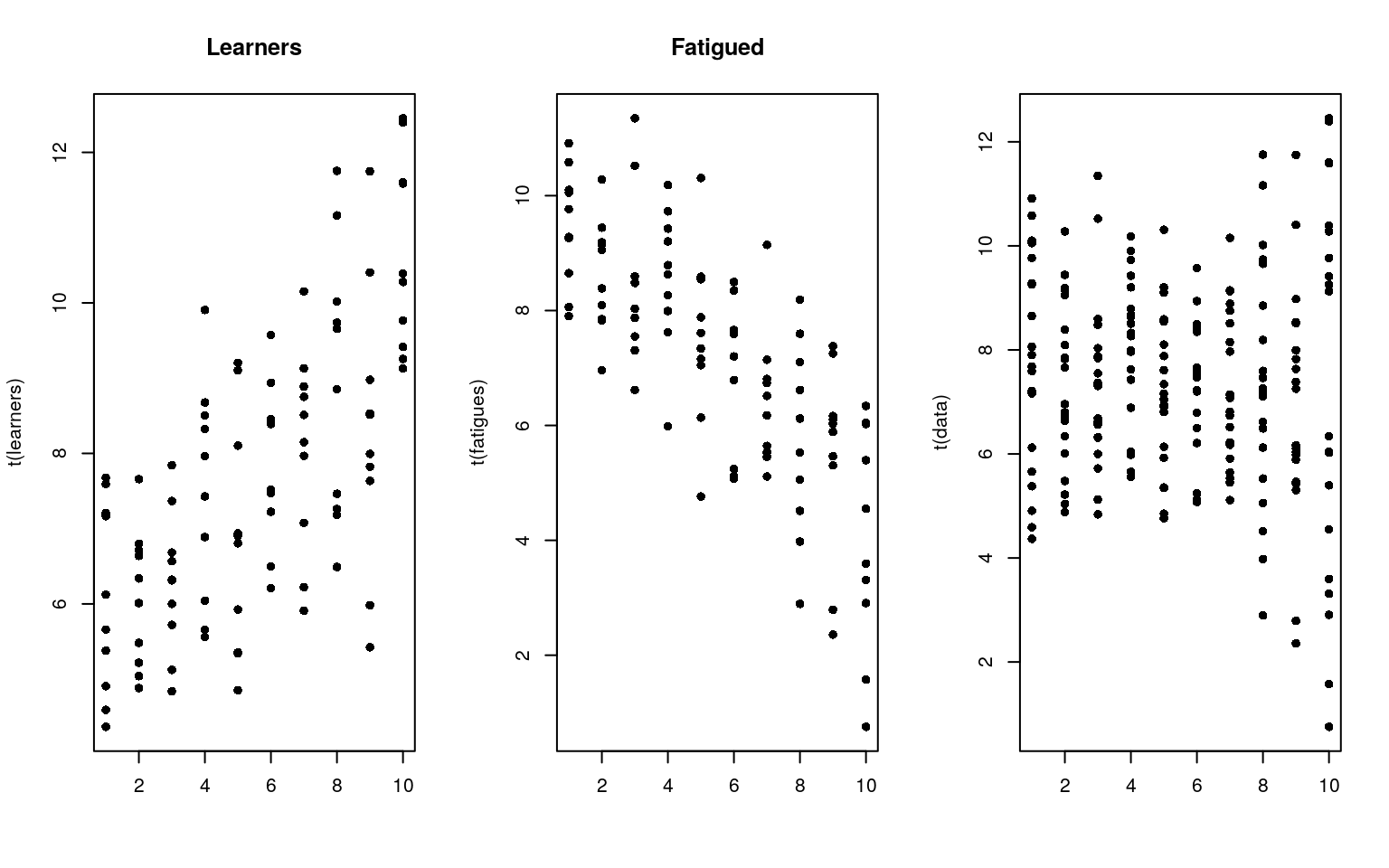

Although we have two different groups, without knowing about their identity, we might just look at the data and declare that they are all the same. Of course, if they were all the same, we would see some that have a positive slope, and some that have a negative slope. Seeing some with positive and some with negative slope doesn’t necessarily tell us we have two groups though. For example, here is a a data set created from a single group

data2 <- matrix(5 + rnorm(200) * 2, 20)

pars1 <- matrix(0, ncol = 2, nrow = 20)
pars2 <- matrix(0, ncol = 2, nrow = 20)
pred <- 1:10
for (i in 1:20) {
    pars1[i, ] <- lm(data[i, ] ~ pred)$coef
    pars2[i, ] <- lm(data2[i, ] ~ pred)$coef
}

par(mfrow = c(1, 2))
plot(pars1, xlab = "intercepts", ylab = "slopes", main = "Two groups")
plot(pars2, xlab = "intercepts", ylab = "slopes", main = "One group")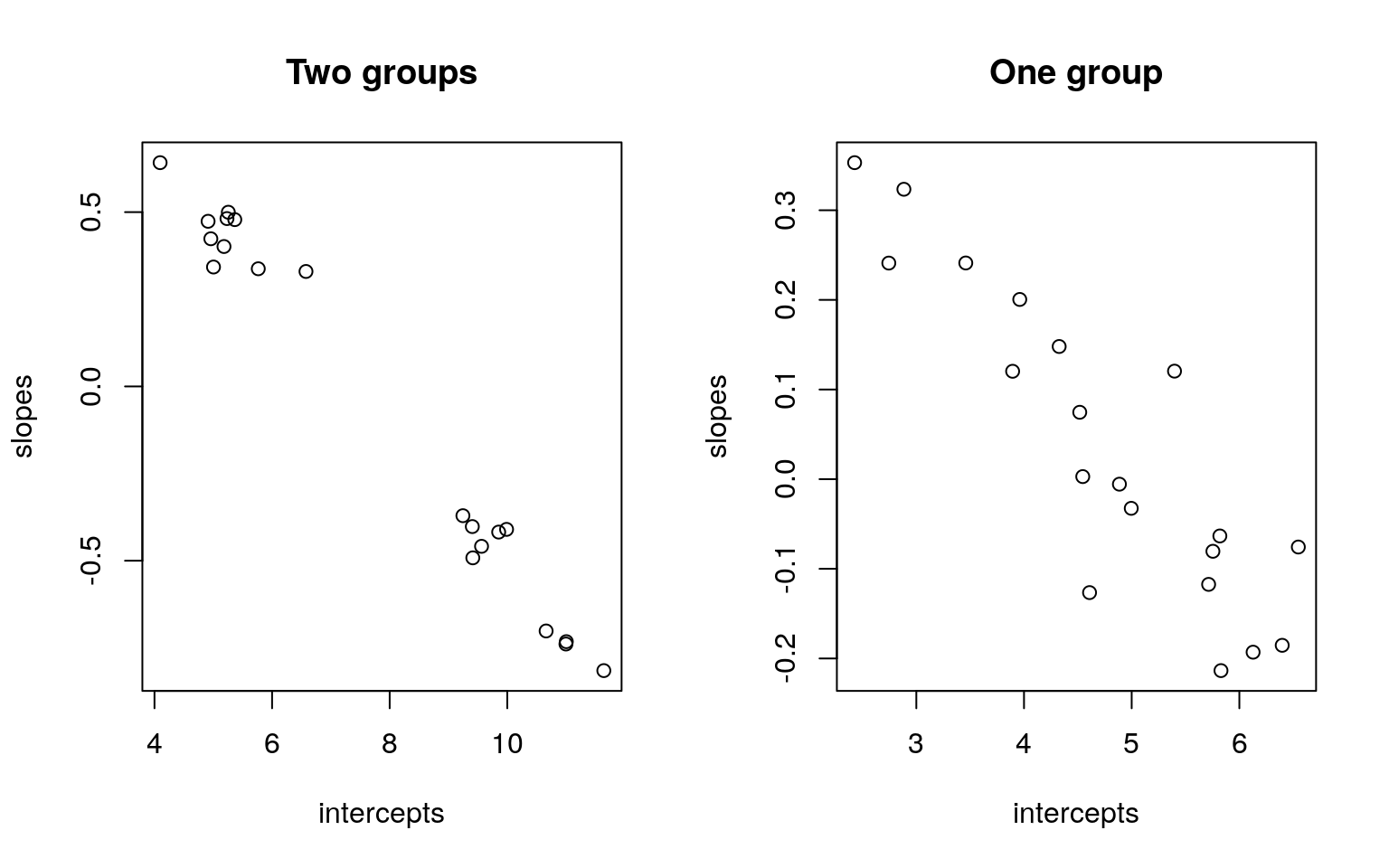

By comparing the slope and intercept of each person, we don’t see a lot of difference. But notice that when we have two groups, that if we fit a regression to each person, the resulting parameters appear to cluster into two groups, with a gap in the middle. When we have one group, they tend to vary more smoothly. A mixture model should be able to take advantage of this.

Howeever, to do so we need to reshape the data

library(reshape2)
data <- as.data.frame(data)
data$sub <- 1:20
long <- melt(data, id.vars = c("sub"))
long$time <- rep(1:10, each = 20)

long[1:10, ]

   sub variable    value time
1    1       V1 5.378643    1
2    2       V1 5.659563    1
3    3       V1 7.207932    1
4    4       V1 4.366967    1
5    5       V1 7.165524    1
6    6       V1 4.906848    1
7    7       V1 6.122199    1
8    8       V1 7.593066    1
9    9       V1 7.678019    1
10  10       V1 4.591429    1

Here, each predictor variable and subject are fitted separately. Now, we can make a repeated-measures regression with the following formula, which will aggregate across subject–exactly what we want. The points of each subject are classified all-or-none into one or the other cluster.

f <- flexmix(value ~ time | as.factor(sub), data = long, k = 2, control = list(iter.max = 10))
parameters(f)

                    Comp.1     Comp.2
coef.(Intercept) 5.2348371 10.1773288
coef.time        0.4410303 -0.5539204
sigma            1.4156778  1.3967110

clusters(f)

 [1] 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2
[36] 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1
[71] 2 2 2 2 2
 [ reached getOption("max.print") -- omitted 125 entries ]

table(clusters(f), long$sub)


     1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20
  1 10 10 10 10 10 10 10 10 10 10  0  0  0  0  0  0  0  0  0  0
  2  0  0  0  0  0  0  0  0  0  0 10 10 10 10 10 10 10 10 10 10

f1 <- flexmix(value ~ time | as.factor(sub), data = long, k = 1, control = list(iter.max = 10))

Example: Curved versus straight models

Mixtures don’t always come from the same process or type of model. Here is a one in which one component is linear, and a second is curved.

x1 <- rnorm(1000) * 5
x2 <- rnorm(1000) * 5
y1 <- 3 * x1 + 10 + rnorm(1000) * 5
y2 <- 10 + 5 * x2 + 0.3 * x2^2 + rnorm(1000) * 5
x <- c(x1, x2)
y <- c(y1, y2)
plot(x, y)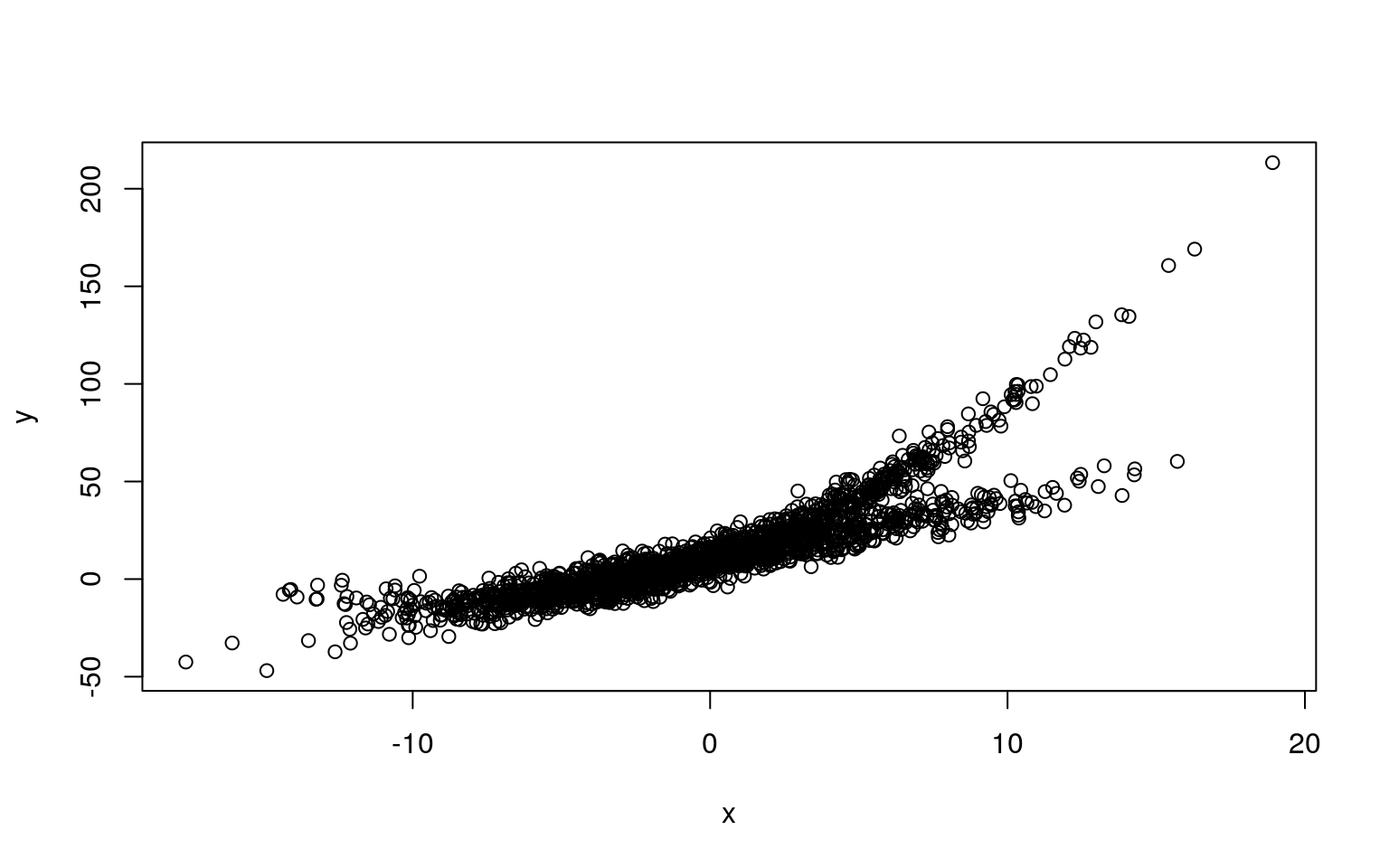

Here, we fit two polynomial models, this might work, because a linear model is just a subset of a polynomial model

model3 <- flexmix(y ~ poly(x, 2), k = 2)
summary(model3)


Call:
flexmix(formula = y ~ poly(x, 2), k = 2)

       prior size post>0 ratio
Comp.1 0.508  981   1874 0.523
Comp.2 0.492 1019   1860 0.548

'log Lik.' -6469.928 (df=9)
AIC: 12957.86   BIC: 13008.26

plot(x, y, col = c("red", "green")[clusters(model3)])

ord <- order(x)
points(x[ord], predict(model3)[[1]][ord], type = "l", col = "black", lwd = 6)
points(x[ord], predict(model3)[[1]][ord], type = "l", col = "red", lwd = 3)
points(x[ord], predict(model3)[[2]][ord], type = "l", col = "black", lwd = 6)
points(x[ord], predict(model3)[[2]][ord], type = "l", col = "green", lwd = 3)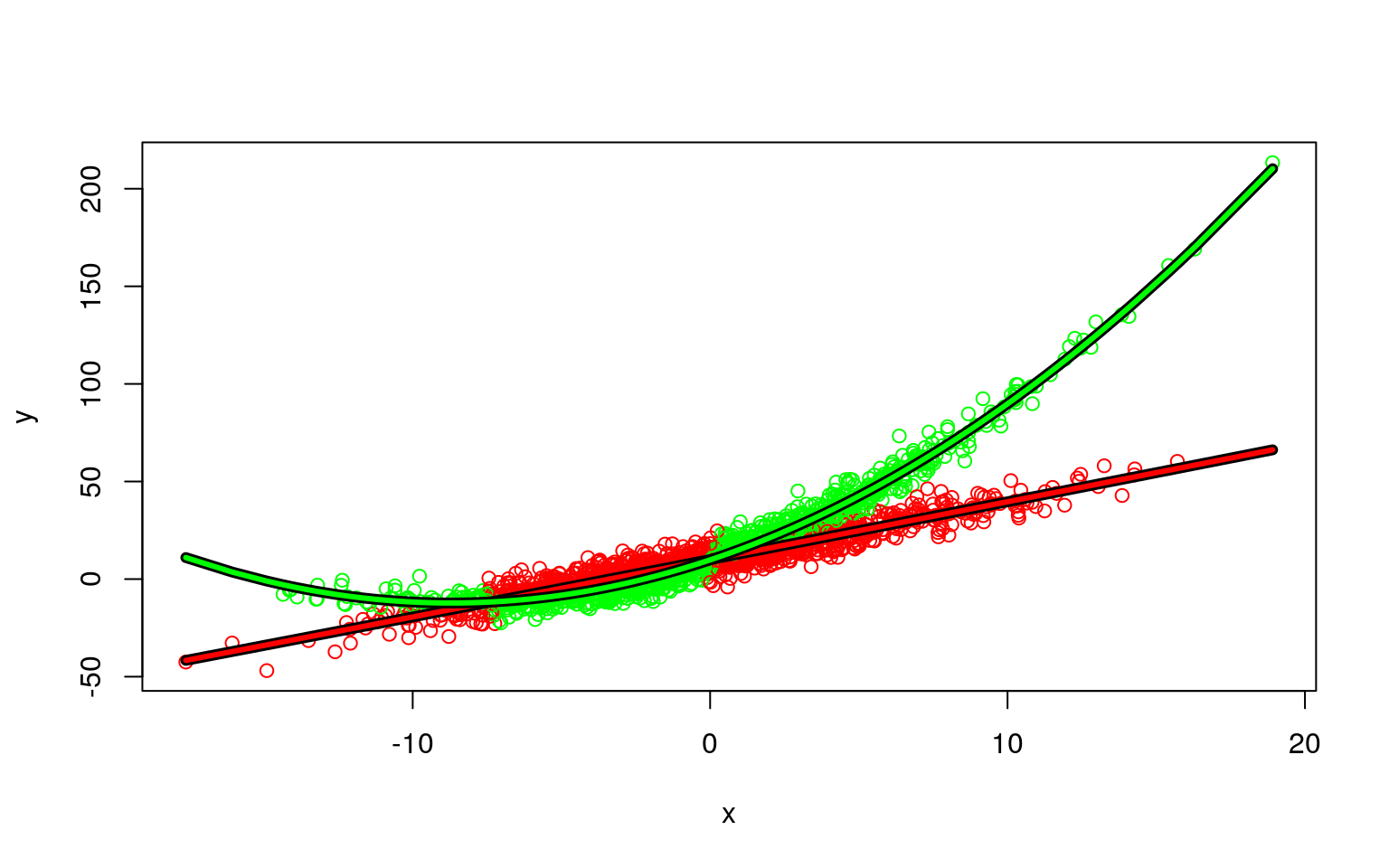

We can look at basic statistical tests with the following trick:

model3 <- flexmix(y ~ poly(x, 2), k = 2)
rm1 <- refit(model3)
summary(rm1)

$Comp.1
             Estimate Std. Error z value Pr(>|z|)
(Intercept)   9.58939    0.23356 41.0567   <2e-16 ***
poly(x, 2)1 666.12313    8.77701 75.8940   <2e-16 ***
poly(x, 2)2   1.90529    8.34082  0.2284   0.8193
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

$Comp.2
              Estimate Std. Error z value  Pr(>|z|)
(Intercept)   16.55557    0.23402  70.743 < 2.2e-16 ***
poly(x, 2)1 1146.34537    8.65023 132.522 < 2.2e-16 ***
poly(x, 2)2  472.43166    7.73804  61.053 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

You can see that for one model, it is quadratic, but for the other the quadratic term is not significant.

Control parameters

If you want to set a maximum number of iterations = 10 in model3,

model31 <- flexmix(y~poly(x,2),k=2,control = list(iter.max=10))

Another control parameter is minprior. it is the minimum prior probability that components are enforced to have. Components falling below this threshold (the current default is 0.05) are removed during EM iteration to avoid numerical instabilities for components containing only a few observations. Using a minimum prior of 0 disables component removal. Here is a regression model with two latent classes. We can compare it to the actual class at the end:

data("NPreg")
m1 <- flexmix(yp ~ x + I(x^2), data = NPreg, k = 4, control = list(minprior = 0.2))
summary(m1)


Call:
flexmix(formula = yp ~ x + I(x^2), data = NPreg, k = 4, control = list(minprior = 0.2))

       prior size post>0 ratio
Comp.1 0.521  122    180 0.678
Comp.2 0.479   78    200 0.390

'log Lik.' -439.1564 (df=9)
AIC: 896.3128   BIC: 925.9977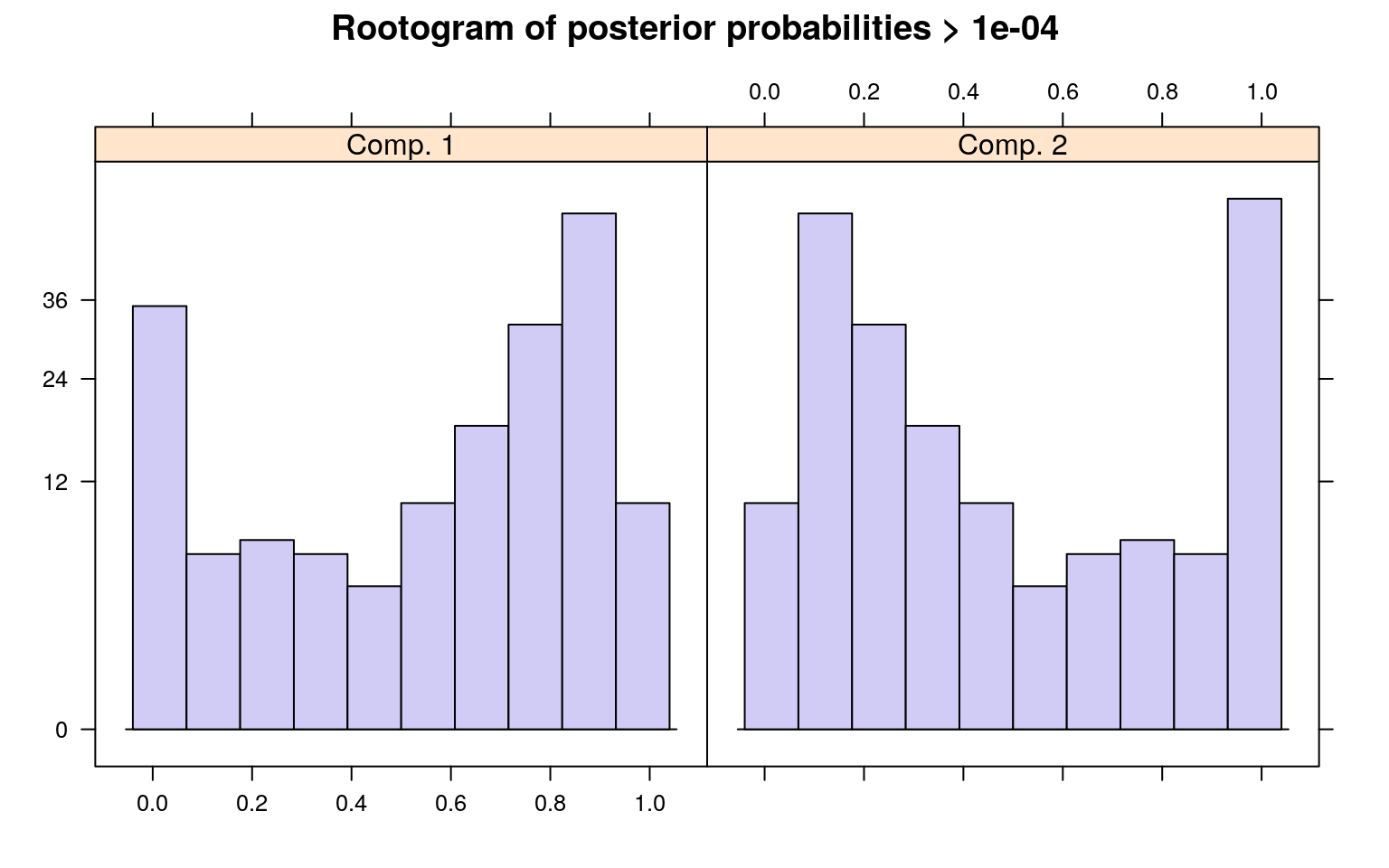

plot(m1)

clusters(m1)

 [1] 1 1 2 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 1 2 2 2 1 2 1 1 1 1 1 2 1 2 2 2 1
[36] 1 1 2 2 1 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 2 1 2 1 1 1 2 1 2 1 1 1 1 1 1
[71] 1 1 2 1 1
 [ reached getOption("max.print") -- omitted 125 entries ]

table(NPreg$class, clusters(m1))


     1  2
  1 75 25
  2 47 53

References

Leisch, F. (2004). Flexmix: A general framework for finite mixture models and latent class regression in R. Journal of Statistical Software, 1-18.