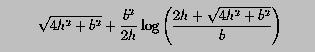
Given base b and height h, the length of a special segment on a parabola can be computed as follows:
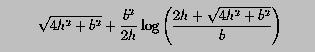
Write a program to read in the values of base and height, and use the above formula to compute the length of the parabola segment. Note that both base and height values must be positive.
![]()
Click here to download this program.! ----------------------------------------------------------- ! Calculate the length of a parabola given height and base. * ! ----------------------------------------------------------- PROGRAM ParabolaLength IMPLICIT NONE REAL :: Height, Base, Length REAL :: temp, t WRITE(*,*) 'Height of a parabola : ' READ(*,*) Height WRITE(*,*) 'Base of a parabola : ' READ(*,*) Base ! ... temp and t are two temporary variables t = 2.0 * Height temp = SQRT(t**2 + Base**2) Length = temp + Base**2/t*LOG((t + temp)/Base) WRITE(*,*) WRITE(*,*) 'Height = ', Height WRITE(*,*) 'Base = ', Base WRITE(*,*) 'Length = ', Length END PROGRAM ParabolaLength
Height of a parabola : 100.0 Base of a parabola : 78.5 Height = 100. Base = 78.5 Length = 266.149445
The input values for Height and Base are 100.0 and 78.5,
respectively. The computed length is 266.149445.
![]()