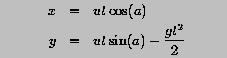
This program computes the position (x and y coordinates) and the velocity (magnitude and direction) of a projectile, given t, the time since launch, u, the launch velocity, a, the initial angle of launch (in degree), and g=9.8, the acceleration due to gravity.
The horizontal and vertical displacements are given by the following formulae:
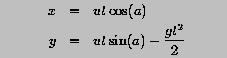
The horizontal and vertical components of the velocity vector are computed as
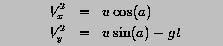
and the magnitude of the velocity vector is
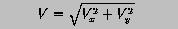
Finally, the angle between the ground and the velocity vector is determined by the formula below:
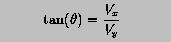
Write a program to read in the launch angle a, the time since launch t, and the launch velocity u, and compute the position, the velocity and the angle with the ground.
![]()
Click here to download this program.! -------------------------------------------------------------------- ! Given t, the time since launch, u, the launch velocity, a, the ! initial angle of launch (in degree), and g, the acceleration due to ! gravity, this program computes the position (x and y coordinates) ! and the velocity (magnitude and direction) of a projectile. ! -------------------------------------------------------------------- PROGRAM Projectile IMPLICIT NONE REAL, PARAMETER :: g = 9.8 ! acceleration due to gravity REAL, PARAMETER :: PI = 3.1415926 ! you knew this. didn't you REAL :: Angle ! launch angle in degree REAL :: Time ! time to flight REAL :: Theta ! direction at time in degree REAL :: U ! launch velocity REAL :: V ! resultant velocity REAL :: Vx ! horizontal velocity REAL :: Vy ! vertical velocity REAL :: X ! horizontal displacement REAL :: Y ! vertical displacement READ(*,*) Angle, Time, U Angle = Angle * PI / 180.0 ! convert to radian X = U * COS(Angle) * Time Y = U * SIN(Angle) * Time - g*Time*Time / 2.0 Vx = U * COS(Angle) Vy = U * SIN(Angle) - g * Time V = SQRT(Vx*Vx + Vy*Vy) Theta = ATAN(Vy/Vx) * 180.0 / PI WRITE(*,*) 'Horizontal displacement : ', X WRITE(*,*) 'Vertical displacement : ', Y WRITE(*,*) 'Resultant velocity : ', V WRITE(*,*) 'Direction (in degree) : ', Theta END PROGRAM Projectile
45.0 6.0 60.0
The program will generate the following output:
Horizontal displacement : 254.558472 Vertical displacement : 78.158432 Resultant velocity : 45.4763107 Direction (in degree) : -21.1030636
![]()