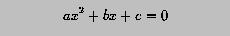
Given a quadratic equation as follows:
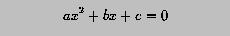
if b*b-4*a*c is non-negative, the roots of the equation can be computed with the following formulae:
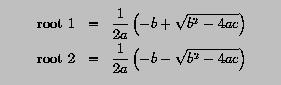
Write a program to read in the coefficients a, b and c, and compute and display the roots. You can assume that b*b - 4*a*c is always non-negative.
![]()
Click here to download this program.! --------------------------------------------------- ! Solve Ax^2 + Bx + C = 0 given B*B-4*A*C >= 0 ! --------------------------------------------------- PROGRAM QuadraticEquation IMPLICIT NONE REAL :: a, b, c REAL :: d REAL :: root1, root2 ! read in the coefficients a, b and c WRITE(*,*) 'A, B, C Please : ' READ(*,*) a, b, c ! compute the square root of discriminant d d = SQRT(b*b - 4.0*a*c) ! solve the equation root1 = (-b + d)/(2.0*a) ! first root root2 = (-b - d)/(2.0*a) ! second root ! display the results WRITE(*,*) WRITE(*,*) 'Roots are ', root1, ' and ', root2 END PROGRAM QuadraticEquation
A, B, C Please : 1.0 -5.0 3.0 Roots are 4.30277538 and 0.697224379
The input to the above problem consists of three real numbers, 1.0, -5.0
and 3.0, and the computed roots are 4.30277538 and 0.697224379.
![]()
After displaying this message, the computer executes READ. Since there is no input value, it will wait until the user types in three real values and hits the Return key. Then, these values are stored in a, b and c.A, B, C Please :