Programming Example 3: Heron's Formula for Computing Triangle Area

Problem Statement

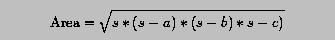
Given a triangle with side lengths a, b and c, its area can be computed using the Heron's formula:

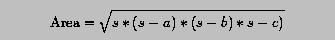
where s is the half of the perimeter length:

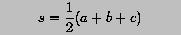
Write a program to read in the coefficients a, b and c, and compute the area of the triangle. However, not any three numbers can make a triangle. There are two conditions. First, all side lengths must be positive:

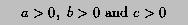
and second the sum of any two side lengths must be greater than the third side length:

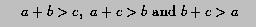
In the program, these two conditions must be checked before computing the triangle area; otherwise, square root computation will be in trouble.

Solution

! ------------------------------------------------------
! Compute the area of a triangle using Heron's formula
! ------------------------------------------------------

PROGRAM  HeronFormula
   IMPLICIT  NONE

   REAL     :: a, b, c             ! three sides
   REAL     :: s                   ! half of perimeter
   REAL     :: Area                ! triangle area
   LOGICAL  :: Cond_1, Cond_2      ! two logical conditions

   READ(*,*)  a, b, c

   WRITE(*,*)  "a = ", a
   WRITE(*,*)  "b = ", b
   WRITE(*,*)  "c = ", c
   WRITE(*,*)

   Cond_1 = (a > 0.) .AND. (b > 0.) .AND. (c > 0.0)
   Cond_2 = (a+b > c) .AND. (a+c > b) .AND. (b+c > a)
   IF (Cond_1 .AND. Cond_2) THEN
      s    = (a + b + c) / 2.0
      Area = SQRT(s*(s-a)*(s-b)*(s-c))
      WRITE(*,*) "Triangle area = ", Area
   ELSE
      WRITE(*,*) "ERROR: this is not a triangle!"
   END IF

END PROGRAM  HeronFormula

Program Input and Output

• If the input to the program consists of 3.0, 5.0 and 7.0, we have the following output. Since the value of all input are positive and the sum of any two is larger than the third (i.e., 3.0+5.0 > 7.0, 3.0+7.0+5.0 and 5.0+7.0>3.0), both conditions hold and the program can compute the area of the triangle. The area is 6.49519062.

  3.0  5.0  7.0
  
  a = 3.
  b = 5.
  c = 7.
  
  Triangle area = 6.49519062
  

• If the input to the program consists of 3.0, 4.0 and 7.0, we have the following output. Although all input values are positive, this is not a triangle since the sum of the first side (3.0) and the second (4.0) is not grater than the third (8.0). The program generates an error message.

  3.0  4.0  8.0
  
  a = 3.
  b = 4.
  c = 8.
  
  ERROR: this is not a triangle!
  

• If the input to the program consists of -1.0, 3.0 and 5.0, we have the following output. Since not all input values are positive, this is not a triangle.

  -1.0  3.0  5.0
  
  a = -1.
  b = 3.
  c = 5.
  
  ERROR: this is not a triangle!
  

Discussion

• This program uses two LOGICAL variables, Cond_1 and Cond_2 to store the results of the two conditions.
• The conditions are checked with the first two assignments.
• Since all side lengths must be greater than zero, operator .AND. are used to connect a > 0.0, b > 0.0 and c > 0.0.
• Since the sum of any two side lengths must be greater than the third side length, all three comparisons must be .TRUE. and operator .AND. is used.
• Since both conditions must be true in order to have a triangle, .AND. is also used in the IF-THEN-ELSE-END IF statement.
• If both conditions are .TRUE., the THEN part is executed, where the value of s and the area is computed and displayed.
• If one or both conditions is .FALSE., the input is not a triangle and an error message is displayed.
• You can pull all six comparisons into a single logical expression. But, this expression could be too long to be fit into a single line. While continuation line can be used, it may not be readable. So, I prefer to have separate lines.